There exists two different families of Magic Meshes. They are called Type 2 and Type 3. Type 2 is the family that Magic Squares belong to, and Type 3 is the family that Magic Hexagons belong to.
Type 2:
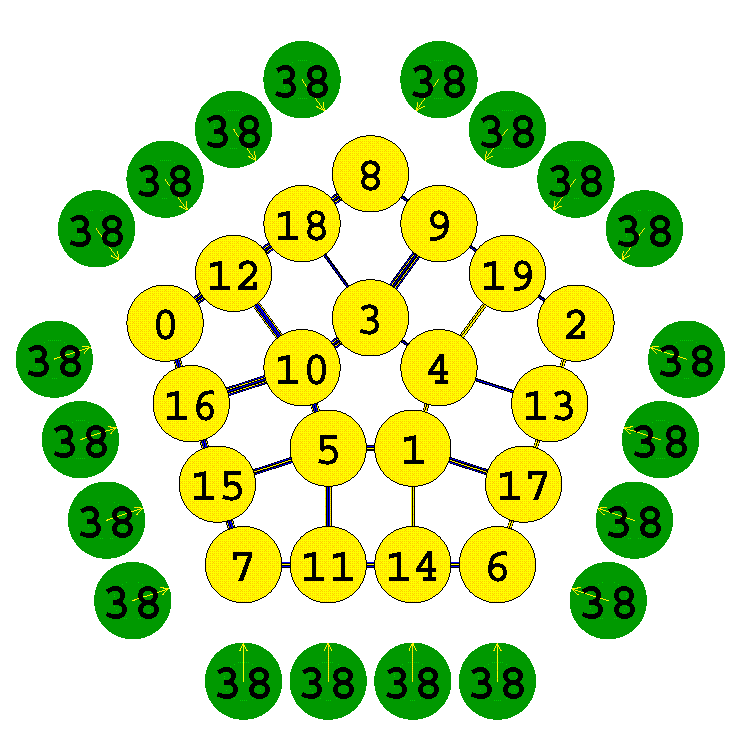
The properties of the Type 2 family are similar to those of Magic Squares, ie.. all rows are identical in length, and add to the same value. You can add a constant value to every cell and the result is still completely magic. Therefore, every Type 2 Magic Mesh that I have generated uses the numbers 0 to k, k being 1 less than the total number of cells in the figure. The following is an example of a 5 sided Type 2 Magic mesh with 4 cells per side:
It uses the numbers 0 to 19 once and only once, and each row of yellow cells adds to 38. Every row is 4 cells in length.
A Type 2, 5 Sided Order 5 follows.
Every row is 5 cells in length, and it uses the numbers 0 thru 30 once and only once. Each row adds to 67. Unlike a regular Magic Square, 67 is NOT the only Magic value that this 5 sided, 5 cells per side Type 2 can add to. It can, using the same numbers 0 thur 30, add to from 67 up to 83. as seen below:
There exists an uncountable total number of Type 2 Magic Meshes, starting with the 960 three sided, 4 cells per side arrangement using the numbers 0 thru 11 that adds to 22.
You can play with some of these if you go here and open any of these PDF files. If your Acrobat reader has Javascript activated, then: Slidey's Page 1 is a puzzle where, once you hit "Reset" the first time, if you move your mouse over the green values, you will see a row highlighted. Press that green cell, and the cell values in the highlighted row will move from one cell to another, fall off the end and come back to the begining. If the green cell has a Large square frame visible, if you hit your "Tab" key, a small square frame will come forward, and if you then click the small square frame, the row values will reverse in their motion. Page 2 consistes of a target solution. You will see that Page 2's green cells all have the same value once you press either the "rotate all" or "reflect all" buttons. You can maneuver the values of Page 1 towards their spots on page 2, however, There is a fifty percent chance that you will need to rotate or reflect page 2 to allow page 1 to be solveable. Tiley's Page 1 is similar to the plastic tile puzzles, ie.. the smallest value is a "blue" square after you hit the reset button. If you then hit the center of any value in one of the same rows that the blue square resides, the row from that selected value will shift toward the open "blue" value, and the blue value will now be in the cell that you just selected. Again, the goal is to get page 1 to match the setup of one of the rotations or reflections of page 2.
Type 3:
Type 3, like Type 2, are a series of n-sided figures nested from outside to inside, with a certain number of cells arranged per figure such that they can be "connected" to form rows that add to the same value. Type 2's cells decrease by 2 as you go from outside to inside, ie... the external row of the previous Type2 5 sided 5 cells per side, consists of 3 figures from outside to inside haveing 5 cps, 3 cps, and the central 1 cps. If a Type 2 had an even number of cells per external side, ie.. 4, it would only consist off 2 geometric figures, a 4 cps and a 2 cps. Type 3 do not decrease by 2, but instead, by 1. All Type 3 Magic meshes have a central single cell, and increase inward to outward by 1. The rows are not identical in length, and so, you cannot transform a type 3 by adding a single constant value to each cell. Type 2 figures can have no diagonals, diagonals, or "diaganoids", that is, a line of cells thaty start on a vertice, pass thru the central cell, and end in the middle of the side opposite the originating vertice. Type 3 can have Diagonals, and "Half Diags", ie... a line of cells that start from a vertice and terminate in the central cell. The following is a 5 sided type 3, with 4 cells per side, using the numbers -45 to -15 once and only once, to add to -144: