LOS NÚMEROS

Aunque no soy matemático siento un interes y aprecio por los números que me ha llevado a escribir por entretenimiento estos comentarios entre la matemática, la lógica, la filosofía y la literatura, el escrito es en cierta medida desordenado e irregular, pero creo que es bastante coherente.

a. Me sorprende darme cuenta de la asimetría que se da en matemáticas con respecto a lo que es considerado número y lo que no. Digamos que parece que:

cero, sea considerado un número lo mismo que 1 ó, a lo más, que unos lo consideren un número y otros no, pero, parece que con:

infinito, hay la mayor confusión y que aunque no sea un número como 1 2 3 se hable de él como si sí lo fuera. En parte es cierto que lo es y que podemos acabar llamándolo número o mejor clase de números, pues, entre otras cosas, se habla de una serie de órdenes de infinitos, en que clasificarían los infinitos, los llamados transfinitos, cuya representación simbólica se basa en la letra alef:

El alef es la primera letra del alfabeto arameo, que es el actual alfabeto del hebreo. Los transfinitos son ordenes numéricos, estos órdenes son más bien propiedades numéricas comunes a diferentes conjuntos de números infinitos y sus finitos correspondientes, siendo los infinitos definiciones de propiedades de clases de números finitos. Razono así:

Quizás, sea posible que habiéndose definido la diversidad respecto de infinito sea posible afirmar que es el nombre propio de una clase de números (que incluiría los infinitos y los transfinitos) y no un número, pero, no sé por qué no parece que ocurra lo mismo con cero e ignoro por qué no parece que haya una serie similar a la de los alef dedicada a diferentes cero o vaciedades, ¿es que habiendo definido los diferentes infinitos y transfinitos no es necesario definir diferentes ceros? Quizás sea así, pero, no se trataría de identificar lo vacío con lo infinitesimal cuando se habla de cero, sino de ordenes de vaciedad relacionados con las definiciones de infinitos codependientes. Si el infinito natural lo definimos como una ley recursiva de paso uno, resulta:

Esta no es la definición de un transfinito, sino de un infinito, que podemos llamar infinito₁siendo 1 el tamaño de paso relativo en los números naturales porque es 1 y porque la ley es la suma o ascendente. Codependiente con ella el cero natural será:

que podemos representar de manera abreviada como: cero₁siendo el subíndice 1 el tamaño de paso absoluto. Si definimos una secuencia de paso más pequeño: X_n+1=X_n+0,1 a la que corresponde el cero: X_n+1 - (X_n+0,1) y, por ejemplo, le sumamos 1, resulta:

1 se ha multiplicado por diez, la vaciedad depende del grado de discreción, piénsese en una secuencia de números raciones como más abajo se explica. Por el contrario si sumamos:

el paso es mayor y se ha dividido por mil. Si uno se pregunta qué resulta de sumar el cero natural y el infinito natural:

la respuesta puede ser distribuir el cero en la igualdad o distribuir la igualdad en el cero. Se hacen operaciones, o así:

resulta el infinito₁: X_n+1 = X_n+1
O, teniendo en cuenta que la igualdad de que tratamos tiene la propiedad de ser recursiva, lo cuál, permite distribuirla en la de la suma, hacer así:

resulta el cero₁: X_n+1- ( X_n+1)
En cierto modo esto, que de la suma de cero e infinito pueda resultar tanto cero como infinito, o cualquier otro número natural ya que estos dos son solo valores extremos, significa que cero o vaciedad e infinito tienen el mismo valor tanto absoluto como relativo que podemos considerar una consecuencia de su codependencia.
Una comprobación más ¿qué ocurre si cero natural es el primer número de la sucesión de los números naturales?:

el siguiente número es el 1. Pero, si el primer número no fuera el cero natural sino otro cero distinto el siguiente número aunque se siga de un paso natural no es el siguiente de los números naturales.
Al tratar de los números enteros volveré un poco sobre el cero.

b. después de mi sorpresa he comprobado, además, que hay números que tienen dos representaciones o ¿quizás una representación y un nombre propio? Me refiero claro está a los números irracionales, los llamados números transcendentes entre los que se hallan elementos como pi, e, i, raiz cuadrada de dos o el número aureo numero cuyo orden es el mayor de entre las clases de números identificadas, cosa paradójica si se piensa que son solo unos muy pocos de ellos los comunmente identificados. No me atrevo casi ni a intentar representarlos mediante los símbolos numéricos porque como es bien sabido cualquier representación mediante estos resulta ser parcial, pues, conocemos solo parte de cada uno de ellos, pero hay una manera de señalar la sucesión de símbolos, los tres puntos. La pregunta que me hago viene a ser así, este símbolo:

donde los tres puntos ... no se pueden quitar sin cambiar la representación y su posible significado. Así que, 3,141..., diré que es un número asociado a tres puntos. Estamos ante un número imprecisable, aunque no impreciso. Pongamos por caso, 3,141; 3,142; 3,1415; 3,1416 son números, pero, si los tomamos como pi deberemos particularizar que son números imprecisos, lo cuál no ocurre con 3,141... , pues, aunque me resulte imposible conocer del todo cómo es pi, sé qué número es porque lo puedo nombrar e identificar con la palabra pi o representar con 3,141.... Esto es asemejable a cuando identifico algo -una cosa o un ser cualquiera- sin más que percibir una parte de ello, sé seguro que es ello sin precisar conocer más que lo percibido o explícito.
Podemos describir lo que ocurre así, en 3,141..., 3,141 representa una parte definida y los tres puntos ... representan una parte indefinida.

pi	3,141...
parte definida	3,141
parte indefinida	...

Podemos decir de los tres puntos ... que es un in-definido, por analogía al in-finito, un infinito no se puede representar mediante símbolos numéricos y un indefinido tampoco, pero, mientras infinito es la tendencia y el orden de una sucesión de números que crecen, indefinido es la tendencia y el orden de un número que crece. Creo que podríamos afirmar ya que los números transcendentes son representaciones complejas o, si deseamos llamar número a un indefinido, entonces, que son números que admiten una composición triple de una parte entera, una decimal y una indefinida.
Nótese que un indefinido no es una parte implícita, sino la explicitación mediante un símbolo de que hay una parte implícita; esto es la explicitud e implicitud se dan en grados.
Con pi y los otros números transcendentes -o irracionales- estamos ante la paradoja de que el número crece hacia un límite desconocido, 3,141... crece pero núnca llega a 3,15 ni ha 3,142 Así, un número transcendente sería un número cuya representación solo se puede lograr mediante una parte de símbolos numéricos y un indefinido de naturaleza entre compleja y aleatoria. Mientras sepamos el principio del indefinido podemos emplear una fórmula para definirlo, así:

Con las X mayúscula sub i represento que se trata del elemento que ocupa la posición i del número obtenido de realizar la operación de la fórmula que precede ante la raya _. Tampoco el indefinido es señal de imprecisión, sugiero que se puede señalar la imprecisión de otro modo, por ejemplo, con un signo de interrogación, en el caso de pi serían representaciones correctas: ?3,141; ?3,142; ?3,1416; pero, sin tal signo de interrogación serían incorrectas o, simplemente: 3,141; 3,142; 3,1416 no representan pi sino tales números. Este signo se continuaría representando en cada número por el que la imprecisión se propaga. Así el área de un círculo de radio 2,5 tomando pi=?3.141592653589793 sería:

c. Pero, mi sorpresa, se cambia en maravilla cuando me doy cuenta de que hay otros números que aunque no tienen un nombre tan propio se suelen nombrar mediante una operación y símbolos numéricos además de representar con símbolos numéricos y el indefinido, algo que ciertamente ya ocurría con raiz cuadrada de 2 (que a falta de poder simbolizar presento con tal frase descriptiva). Me refiero a los números fraccionarios que dan como resultado una serie periódica de símbolos numéricos, que por ser fraccionarios son racionales, aunque su racionalidad queda en entredicho al constatar que la realización de la operación de división no se puede volver atrás con una multiplicación, excepto si definimos la multiplicación en términos de la división previa, pues, por ejemplo:

en este número, tampoco se puede prescindir de los tres puntos ... de indefinido sin amputarle algo suyo y, así, volverlo impreciso. El indefinido en este caso es de un orden diferente que el de los números irracionales, de este es fácil conocer que se trata de la repetición de 3, es un indefinido periódico lo que podemos dejar claro así:

X_i+1=X_iDescribe el indefinido en términos de recursividad, el subindice i aquí se referirá como antes al elemento que ocupa tal posición de número, de otra manera, como antes, se trata de un segmento que es parte de un número. También se puede representar de otra manera, así:

Pero, sigamos, ¿por qué me maravillaba? pues, porque van apareciendo cosas que se parecen entre sí en algo y se diferencian en algo y entre ellas hay como un gradiente entre posibilidad de nombre propio y posibilidad de solo representación en símbolos numéricos. De manera que podemos afirmar que:

d. en el extremo los números naturales y, por así decirlo, sus nombres propios son una misma representación en símbolos numéricos. Así, por ejemplo:

es nombre del número que representan los tres símbolos numéricos puestos como están en sucesión. Se podría representar con unos y ceros, en sistema binario o en algún otro sistema, pero no cambiaría mas que el lenguaje o sistema de símbolos empleado.

se trata de un número natural cuyo nombre es su misma representación en símbolos numéricos y aquí, como, en

cuyo valor cabe preguntarse si es solo gramatical, digamos que sintáctico, o si significa algo por sí solo. Es fácil ver en el segundo que solo tiene valor sintático, pues, si prescindimos de él, aún, nos queda la coma ",333...", o el punto ".333..."en la otra notación y, esta coma, es suficiente para saber que se trata de un decimal.

Pero, por comparar con el lenguaje, de la frase: el niño juega, la palabra el (como en ¡Él!), la palabra niño (como en ¡Níño!) o la palabra juega (como en ¡Juega!) pueden llegar a significar algo por sí solas, pero, ni el fragmento el (no tiene acento) ni la frase fragmentaria niño juega lo pueden hacer : el por un lado y niño juega no significan nada por sí solos sino como elementos sintácticos en una oración como: el niño juega. Esto es cabe preguntarse si cero es el nombre de tal símbolo y utilizado para escribir números o, como cosa diferente, si con el debido contexto puede llegar a ser es el nombre de un número. Pues, por ejemplo, hay palabras como me que por sí solas no generan una oración precisa.
Pero, ¿qué ocurre con el cero de 340, es un número o solo tiene valor sintáctico?

f. Pienso en que hay números llamados negativos, algunos de los cuales son enteros como los naturales y que parece que precisamente este cero es la transición de los unos a los otros, así:

No se ponen puntos suspensivos sino el símbolo de infinito, que en este caso he sustituido por la palabra infinito, la razón es que estoy tratando de infinitud de las secuencias de números y no de indefinición de un número, aunque, en cualquier caso el sentido y la denotación sea de incompleción y se señala explícitamente algo implícito.
Pero ¿por qué no se representan así?:

pues porque desde -1 a 1 pasan dos unidades, digamos que se pasa de carecer de uno a satisfacer la carencia y luego se pasa de la satisfacción a disponer de uno sobrante. ¿Quiere esto decir que 0 es un número? creo que no, creo que por no ser, por ser vacío, no es ni siquiera un número ¡qué difícil es entender lo que es estar satisfecho o ser feliz! Podríamos definir el cero como el paso intermedio de la sucesión ascendente de los números negativos a la sucesión ascendente de los enteros positivos o viceversa el paso intermedio de la sucesión descendente de los números enteros positivos a la sucesión descendente de los números enteros negativos. El cero es como un espejo o un vórtice donde se pasa de la una a la otra. Propiamente no pertenece a ninguna de las dos, sino que es el límite o punto al que tienden siendo máximo para los negativos y mínimo para los positivos. De nuevo el cero no parece cumplir más que una función sintáctica, aunque insustituible en esta ocasión, no nombra un número sino que denota un lugar extraño. Más a favor de esto:

sucediendo y y así sucesivamente señalan precisamente que se trata de una sucesión de sucesiones incompleta por ambos extremos. Cómo se puede apreciar la distancia entre el mayor número negativo y el menor número positivo se hace cada vez menor, pero cero como el vórtice que es, por ejemplo, el ojo de un huracan permanece aparentemente fijo.

También, parece que el más y el menos infinito sean otros límites, pero, en mi opinión, está menos claro. Cabe pensar que como hemos definido infinito e indefinido:

El límite sería el final de la sucesión o lo que es lo mismo el lugar de la compleción de toda ella en que se habría de volver al principio. Sin embargo, en este caso solo conocemos un, aparentemente, límite de esta clase para la sucesión de que tratamos en su centro: el cero los otros dos extremos no están señalados como límites sino como un movimiento carente de límite o hacia ningún límite. Si consideramos que hay una totalidad de la sucesión el único punto absoluto en que la sucesión contacta con ella es el cero, podemos obtener, entonces, una figura así:

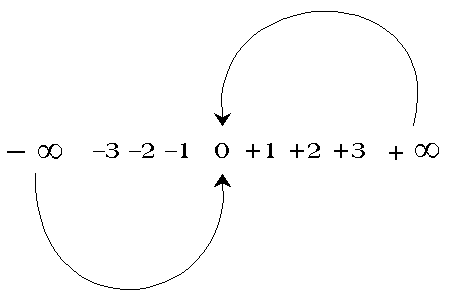
En la totalidad la sucesión vuelve a comenzar. La sucesión gira en torno al cero que permanece quieto, mientras los infinitos permanecen en movimiento. Esta sería la representación de la sucesión completa.Puede pensarse que las unidades discretas al ir alcanzando la sucesión numeros grandes y luego enormes se hacen pequeñas y luego ínfimas hasta que la sucesión se transforma en una sucesión de diferentes sucesiones conectadas a esta a la vez que se vuelve sobre sí misma, resulta sin duda una paradoja del conocimiento que en algún punto la continuidad y la discontinuidad sean compatibles, tal punto es donde se completa la sucesión y la conexión de la sucesión con las otras sucesiones y es por naturaleza desconocido, aunque sepamos de él. Si en esta sucesión definimos -infinito como:

Ambas definiciones describen una relación de discreción codependiente con el cero en términos de recursividad, y la sucesión completa queda definida así:

El tipo de transformación que se da cuando no solo se tiende, sino que se llega a completar la sucesión es en una pequeña parte, por ejemplo, como la sucesividad más arriba explicada, algo así:

-INMENSAS -infinito -3 -2 -1 -infinito -0,3 -0,2 -0,1 -infinito -0,03 -0,02 -0,01 -infinito -0,003 -0,002 -0,001 -INFIMAS 0 +INFIMAS +0,001 +0,002 +0,003 +infinito +0,01 +0,02 +0,03 +infinito +0,1 +0,2 +0,3 +infinito +1 +2 +3 +infinito +INMENSAS

tal y como son las sucesiones particulares de este ejemplo es evidente que las sucesiones internas iran tocando los puntos de las más externas, además, iran apareciendo otras sucesiones tanto próximas a cero como en los extremos, es decir próximas a todo, las cuatro palabras en mayúscula señalan tales nuevas sucesiones. En el centro, se ve cero entre los símbolos -INFIMAS y +INFIMAS. Las sucesiones más ínfimas son sucesiones con ordenes numéricos mayores de segmentos más pequeños, las sucesiones inmensas son sucesiones con órdenes numéricos menores de segmentos más grandes.
Evidentemente la realidad es aún más compleja, en ella se incluye todo, además de, los tipos de números, se incrustan sucesiones como X_n+1=X_n+X_n/2 y hay puntos rellenados por números trascendentes de cuáles no se sabe que formen parte de alguna sucesión, quiero decir que no lo sé, y hay expresiones algebraicas, fórmulas, palabras hasta el lenguaje y el resto de la realidad relacionada, a su vez, con la verdad.
En fin, tras esta larga disgresión, lo que creo que interesa destacar es que el símbolo de cero y los de infinito e indefinido propiamente no representan números sino de manera respectiva:

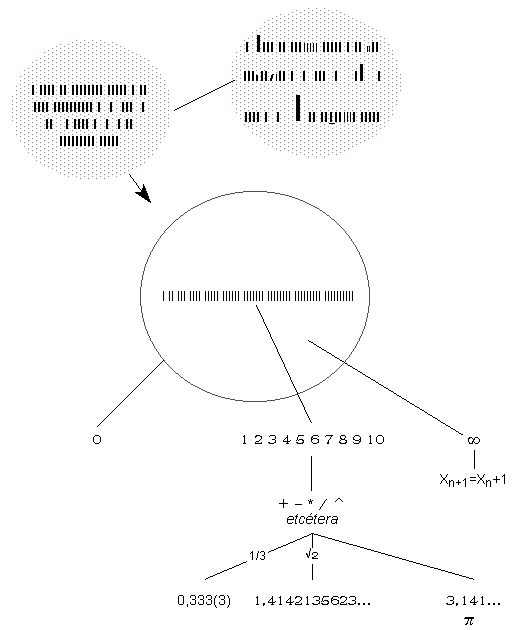
El cero proviene de la consideración del continuo y el absoluto, que son lo mismo, los números provienen de la consideración de lo discreto, el infinito proviene de la consideración de la relación entre lo discreto y el absoluto o continuo y asimismo lo indefinido provendría de la relación de un número con el absoluto o continuo, aunque esto último no se ha representrado.

g. Los nombres de los números y los números se relacionan de manera diversa, dándose deslizamientos del sentido y denotación, se consideran números las representaciones más relevantes en cuanto tales y nombres los que refieren a tales representaciones y que por deslizamiento en lo que viene a ser una metonímia los acabn sustituyendo.

	natural
nombre	1 2 3 4 5	infinito
número	I II III IIII IIIII
sucesión		X_n+1=X_n+1

Por ejemplo, para los números naturales resulta más relevante la representación mediante palotes que usándo los símbolos de origen indio, inclusive aunque en los tres primeros 1 2 3 sea clara la analogía simbólica de la grafía: un trazo vertical en la grafía <1>, dos trazos horizontales en <2>, y tres trazos horizontales en <3>. A pesar de esto he preferido llamar número a la representación más analógica y nombre a la realizada por los símbolos más abstractos, que en parte se han vuelto más arbitrarios.
Por separado he incluido bajo la palabra sucesión la definición del infinito de los números naturales. Está expresada como una relación recursiva o iterativa entre cada dos elementos consecutivos de la sucesión. No se señala el primer elemento porque en los números naturales se trata de una relación absoluta de lo discreto con el continuo, pero, evidentemente en otras sucesiones cabe que sea preciso señalarlo. La interpretación más relevante de tal relación comienza sin duda en 1. Estos infinitos, a veces, se ha creído que son ún lugar o un tiempo, yo diría que son algún lugar y algún tiempo variable, no representan ni son números sino que representan y son una propiedad recursiva numérica que nos indica dónde podemos encontrar números.

		entero
nombre = operación numérica	-infinito	-3 -2 -1 0 +1 +2 +3	+infinito
número		- III II I · I II III +
sucesión	X_n-1=X_n-1		X_n+1=X_n+1

El paso a los números enteros supone introducir la operación de negación, que da los números negativos, con esto se da un importante deslizamiento conceptual. Un número negativo se puede entender como una carencia, los he representando como una sucesión con un signo menos en su extremo, en oposición y codependientes tenemos los números positivos que podemos entender como un sobrante, son los representados como una sucesión con un signo más. El punto es un estado de satisfacción donde ni falta ni sobra nada. Nótese que en los nombres se indica que el nombre incluye la señal de la operación numérica. Por otra lado, el cero queda entre ambas sucesiones y a diferencia del punto y los números apenas se diferencia en su figura de los nombres, no obstante, no lleva el símbolo de ninguna operación.

		absoluto
nombre = operación numérica	\|-infinito\| \|+infinito\|	\|+3\|\|±2\| \|1\|\|-3\|
número		III II I III I II
sucesión	X_n=X_n

Los llamados números absolutos son unos muy peculiares, se podrían llamar indeterminados. Cada número puede estar representando dos veces, una con signo + y otra con signo -, o una sola vez, con doble signo o sin signo, no se da ninguna sucesión se reparten al azar, su infinito permanece moviéndose en el cero, lanzando números en todas direcciones, cada número mantiene absoluta discreción es decir relación absoluta con el continuo. Son lo números más discretos que hay :-)

	racional
	exacto		periódico
nombre = operación numérica	1/2	- 2/5	1/3	5/7
nombre = operación numérica	I_/_II	II_/_{IIIII -}	I_/_III	IIIII_/_IIIIIII
número	0,5	- 0,4	0,3(3)	0,714285(714285)

Los nombres en el caso de los racionales son la representaciones de operaciones con números, no podemos considerar ya que una operación en que interviene más de un número sea un número. Con los números racionales se produce, pues, un importante deslizamiento simbólico, representar los números con palotes aún sería posible usando palótes de diferentes tamaños, sin embargo, esto no es tan fácil y sí es fácil confundir los tamaños o los grosores, asimismo, representar los decimales de un número cuando son muchos podría requerir de una cantidad de palotes diferentes bastante considerable. Para representar los decimales es preciso introducir algunos diacríticos uno para señalar dónde comienzan los decimales, que suele ser la coma o el punto, y cuando los decimales forman una sucesión indefinida -sucesión que podemos llamar interna- se requiere representar la parte que se repetiría, para esto se incluyen los paréntesis. Con todo esto me decido a llamar números a las representaciones con los símbolos de origen indio y nombres a las representaciones de las operaciones que los originarían, sin embargo, nótese que las operaciones son más figurativas o analógicas que los números mismos, pero, repito: no podemos considerar ya que una operación en que interviene más de un número sea un número.

		irracional
nombre	operación numérica	raiz cuadrada de 2
	letra		pi
número		1,414...	3,141...

Dentro de los números irracionales entramos en un nuevo sistema de nomenclatura. Hay algunos números racionales que podemos nombrar por el sistema de representar y describir la operación que los origina, este es el caso de raiz cuadrada de dos, pero para otros se utilizan letras de algún alfabeto, el griego o el latino, tales son pi, e, i o inclusive un nombre como número áureo es de un número irracional. Y se utiliza un nuevo símbolo entre diacrítico y numérico, los tres puntos, que hemos llamado indefinido. Estos tres puntos representan el indefinido es decir la sucesión interna hacia la compleción del número, en el caso de 1,414... los tres puntos se pueden sustituir por la representación de la operación de hallar el elemento X en la posición i de hacer la raiz cuadrada de dos, por ejemplo, se me ha ocurido hacerlo así:

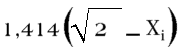
No me parece que un indefinido sea una parte de número sino una propiedad de una parte de un número.

h. Como se ha podido apreciar no he concedido ni a los indefinidos ni a los infinitos el nombre de número, sino solo el ser nombres numéricos. El matiz es importante, digo que los indefinidos no son partes de un número y que los infinitos no son números, sino respectivamente nombre de una parte y nombre de un número. Del mismo modo que si tengo un plátano al que falta una parte y digo que el plátano se completa con la parte que falta no pretendo que l-a p-a-r-t-e q-u-e f-a-l-t-a sea un trozo de plátano, pero, l-a p-a-r-t-e q-u-e f-a-l-t-a tiene la virtud de nombrar lo que falta del plátano. Cuando hablámos de indefinidos y de infinitos nos podemos preguntar ¿cómo son? precisamente porque no son lo que representan. En matemáticas no se acepta, por ejemplo, afirmar algo como: el mayor número natural es el infinito, por lo mismo si decimos: un número infinito o si decimos que tal número tiende a infinito no estamos hablando de un número, sino que se trata de una metonimia, queremos decir un número enorme desconocido y esto se demuestra en que se suele aceptar que si al infinito se le suma o resta un número cualquiera que sea conocido, que sea conocido es una condición indispensable para la regla, seguirá siendo infinito como seguiría siendo enorme un número enorme desconocido. Pero esto, si somos rigurosos, resulta en que tal infinito o un número enorme desconocido siempre es impreciso. Resulta una versión de la paradoja de Wang, que tendría como consecuencia que cualquier número desconocido podría ser considerado ínfimo o enorme y como el ser desconocido o conocido es algo contingente cualquier número podría acabar siendo considerado ínfimo o enorme. Además, hay sucesiones como:

que sabemos a qué tienden, en este caso a 1 para la que podríamos decir, haciéndo una metonimia, que su número infinito es 1 o sin metonímia que tiende a 1. Mucho del problema está en creer que el vacío del cero se puede llenar sumando, pero, en realidad el cero ni se llena ni se vacía. Si postulamos que hay algo como un número infinito estamos afirmando que hay un tercer factor a parte del continuo y de lo discreto, y lo único que podemos considerar como tal cosa es una relación, la relación entre el continuo y lo discreto. Así, nos queda la alternativa de aceptar un nuevo deslizamiento del significado de la palabra número, en que la expresión de la relación entre el continuo y lo discreto sea considerada ya una parte de un número ya un número.

		indefinido	infinito
nombre	letra		infinito natural
número		log₁₀ 4/log₁₀ 3_X_i	X_n+1=X_n+1

Nótese, por último que aunque así damos un significado propio a las expresiones número infinito y parte numérica indefinida, la expresión tender a infinito sigue siendo impropia o si se prefiere es una metonimia. Propiamente no se tiende a infinito, tan solo se es infinito, incompleto, inacabado, insaturado resulta absurdo decir que algo tiende a inacabado si no es lo que se quiere decir. Personalmente prefiero pensar que la infinitud es como el cero una relación de la secuencia con el todo, como es, también, el sujeto la relación del objeto con el todo o absoluto. Una sucesión de números creciente tiende al número lleno, que no es el límite, pero tiene su mismo valor, sin superponerse a él. En la sucesión de los números naturales el lleno no es otro que el vacío, pues, si lo discreto se aproxima a lo continuo el número se hace cada vez mayor y si se funde lo discreto con lo continuo el vacío se llena y lo lleno se vacía.

Bibliografía: En la siguiente bibliografía no se encontrará mucho directamente relacionado con lo explicado, excepto quizás en las obras de George Ifrah y Gottlob Fregue, pero en tales obras hay ideas que se relacionan con lo explicado o lo contextualizan.

John Briggs y F. David Peat (1989): Espejo y reflejo, del Caos al Orden. Traducción de Carlos Gardini Editorial Gedisa, 1990 Barcelona.
Maria Josep Cuenca y Joseph Hilferty: Introducción a la Lingüística Cognitiva. Editorial Ariel, 1999 Barcelona.
Gottlob Fregue (1891-1923): Ensayos de semántica y filosofía de la lógica. Edición, introducción,traducción y notas de Luis M. Valdés Villanueva. Editorial Tecnos, 1998 Madrid.
Manuel Garrido (1995): Lógica Simbólica. Editorial Tecnos, 1997 Madrid.
Georges Ifrah (1985): Las Cifras, historia de una gran invención. Alianza Editorial, 1987 Madrid.
Benoit Mandelbrot (1984): Los objetos fractales. Traducción de Josep Llosa. Tusquets editores, 2000 Barcelona
Platón (siglo V antes de Cristo): "Crátilo" en Diálogos de Platón II. Editorial Gredos, 1999 Madrid.