21 Oct 2001
 ngle Between 2 Vectors
ngle Between 2 Vectors
Let a and b be two non-zero vectors represented by OA and OB respectively. The angle between a and b is defined to be the angle between OA and OB, i.e. �
AOB.
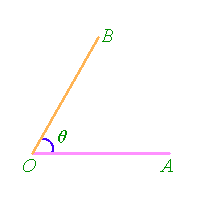 Note that 0� �
� AOB �
180�.
Note that 0� �
� AOB �
180�.

 efinition of Scalar Product
efinition of Scalar Product
The scalar product of two non-zero vectors
a and b, denoted by a.b, is defined as
�
| a.b = |a||b|cos q,� |
where q = angle between a and b.� |

 mportant Properties
mportant Properties
-
a.b = 0 � a ^
b (if a � 0, b
� 0)
-
|a.b| = |a||b| �
a // b (if a � 0,
b � 0)
-
a.b = b.a
-
a.(b + c) = a.b + a.c
-
(la).b = l(a.b)
= a.(lb) where l
� R.
-
a.a = |a|2
: a.b = a.c
does not imply b = c.
For the 3 mutually perpendicular unit vectors
i, j, k, we have
�
| i.i = j.j = k.k = 1 |
| i.j = i.k = j.k = 0 |

 calar Product in Cartesian Form
calar Product in Cartesian Form
Let a = a1i + a2j
+ a3k, b = b1i
+ b2j + b3k.� Then,
using the properties of scalar product, we have
| �a.b |
= |
(a1i + a2j
+ a3k).(b1i +
b2j + b3k)� |
| � |
= |
(a1i + a2j
+ a3k).(b1i) +� |
| � |
� |
(a1i + a2j
+ a3k).(b2j) + |
| � |
� |
(a1i + a2j
+ a3k).(b3k) |
| � |
= |
a1b1 + a2b2
+ a3b3 |
Hence
�
����
| � |
a1 |
� |
� |
b1 |
� |
� |
� |
| �
� |
a2 |
�. |
� |
b2 |
� |
�=� |
a1b1 + a2b2
+ a3b3� |
| � |
a3 |
� |
� |
b3 |
� |
� |
� |
� |

 pplications of Scalar Product
pplications of Scalar Product
1.��� To prove any two non-zero vectors are perpendicular
�
2.��� To find the angle between two non-zero vectors.
�
���
| � |
� |
a.b |
| cos q |
�=� |
---- |
| � |
� |
|a||b| |
� |
3.��� To find the projection of one vector on another.
�
| Length of projection of a on b
= |a.b^| |

 To Other Sites
To Other Sites

 �
�




 ngle Between 2 Vectors
ngle Between 2 Vectors
 efinition of Scalar Product
efinition of Scalar Product mportant Properties
mportant Properties calar Product in Cartesian Form
calar Product in Cartesian Form pplications of Scalar Product
pplications of Scalar Product To Other Sites
To Other Sites