 |
 |
|
|
ree Vectors & Position VectorsA vector that has no specific position in space is called a free vector.
Consider the position of a point A relative to a fixed origin O.� OA is called the position vector of A relative to O.� This displacement is unique and cannot be represented by another line.
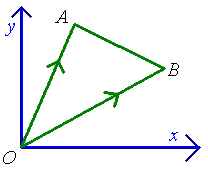
Note:� Any vector AB can be written in terms of the position vectors of A and B:
calar MultiplicationLet a be a non-zero vector and k be any real number. We define a new vector, ka, as follows.
(a) If k = 0, the ka = 0.
(b) If k > 0, the ka has the same direction as a and |ka| = k|a|.
(c) If k < 0, the ka is in the opposite direction to that of a and |ka| = -k|a|.
For all vectors a and b and all scalars l and m, we have:
(a) l(ma) = (lm)a,
(b) (l � m)a = la � ma,
(c) l(a � b) = la � lb.
nit Vectors(a)� A unit vector is a vector with a magnitude of one unit.� A unit vector in the direction of a will be typed as .
(b)� Any vector r can be expressed as the product of its magnitude and the unit vector in the same direction: r = |r|r^
(c) Three important unit vectors are defined as follows:
atio Theorem�
If a point P divides a line segment AB in the ratio m : n, then�
��  |
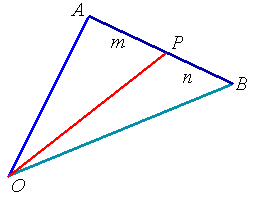Note:� If M is the mid-point of AB, then OM = (OA + OB)/2.
VectorsIf P(a, b, c) is any point in 3-D Cartesian space, then the position vector of the point P is OP = p where
�
| � | a | � | |
| (a) p = ai + bj + ck or� | � | b | � |
| � | c | � |
(b) |p| = (a2 + b2 + c2)1/2
= d
�
| � | a/d | � | |
| (c) p^ = p/|p| =� | � | b/d | � |
| � | c/d | �� |
ome ResultsA��� Parallel
| Let a and b be non-zero vectors.�
Then a is parallel to b if and only if |
B��� Collinear
| Three points A, B and C are collinear if and only
if
|
C��� Coplanar
| Let a and b be non-zero, non-parallel vectors.
A vector c is coplanar with a and b if and only if |
To Other Sites
�