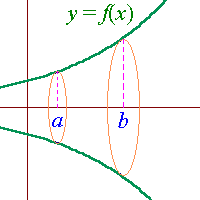-
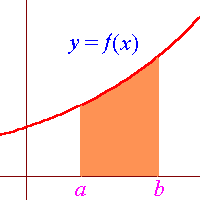
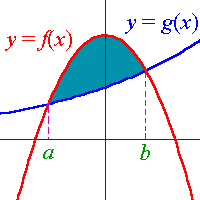
The area bounded by the curve y = f(x), the vertical
lines x = a, x = b, and the x-axis is
given by
| A = |
ób
õa |
y dx |
= |
ób
õa |
f(x) dx. |
-
If the equation of the curve is given in parametric form x
= g(t), y = h(t), then
| A = |
ób
õa |
y dx = |
óv
õu |
h(t)g'(t) dt |
where u and v are the values of t when x
= a and b respectively.
|
 |


 lane Areas
lane Areas
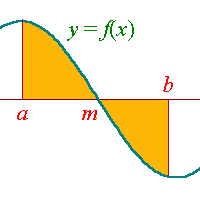
 olumes of Revolution
olumes of Revolution