Basic Concepts Injective, Surjective, Bijective Inverse Function Composite Function Examples

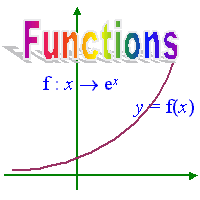
asic Concepts

A function f : X � Y is a rule which associates each element x � X with a unique element y � Y such that y = f(x).

• The set X is called the domain of f and is denoted by D_f .
• The set Y is called the codomain of f.
• f(x) is called the image of x under f or f-image of x.
• The set { f(x) : x � X } is called the range of f and is denoted by R_f .� It is the set of all images of x under f.
• Range of f is a subset of Y, ie, R_f � Y.
• From the graph of f, f is a function if every vertical line x = a for each a � X cuts the graph of f at only one point.

njective, Surjective, Bijective

• A function f : X � Y is said to be injective or one-one if no two distinct elements of X have the same f-image, ie, f(x₁) = f(x₂)� �� x₁ = x₂� for x₁, x₂ � X.

• A function f : X � Y is said to be surjective or onto if for every y � Y, there is at least one x � X such that y = f(x), ie, R_f = codomain of f.

• A function f : X � Y is said to be bijective if it is both one-one and onto.

nverse Function

For every bijective function f : X � Y, there exists an inverse function f^-1 : Y � X such that

• Domain of f^-1 = Range of f.
• Range of f^-1 = Domain of f.
• The graph of the inverse y = f^-1(x) is the reflection of the graph of y = f(x) in the line y = x.� Same scale must be used for both axes.

omposite Function

Let f and g be functions.
Then the composite gof, or simple gf, is defined by

• gof is a function if R_f � D_g.
• D_gof = D_f .
• R_gof � R_g.

xamples

Example 1:  Two functions are defined as follows:

For each of the functions, state the range and determine whether or not the function is one-one.
Give, in the same form, the definition of the functions gof and g^-1.

Solution:

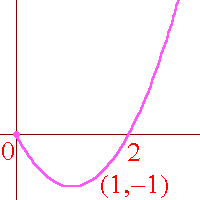	x2 - 2x �=� x(x - 2) �=� (x - 1)2 - 1. Rf = [-1, �).� f(0) = 0 = f(2)� but� 0 � 2. \� f is not one-one.
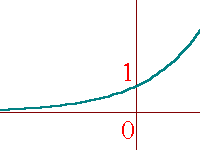	Rg = R+ = (0, �).� g is one-one,� as every horizontal line y = b, b � R, cuts the graph of y = g(x) at most once.

gf(x)	�=�	g(x2 - 2x)
�
	�=�	2x2 - 4x e

\� gof : x �

2x2 - 4x e

, x � R, x � 0.

Let y	�=�	e2x
ln y	�=	2x
x	�=�	�ln y

\� g^-1 : x � �ln x, x � R⁺.

Example 2:  The functions f and g are defined by

Show that fog is a function.� Define fog and state its range.� Explain why the function gof does not exist.

Solution:

R_g = R⁺, D_f = R⁺,
\� R_g � D_f� �� fog is a function.

fog(x) �=� f(1 - x) �=� ln (1 - x) \� fog : x � ln (1 - x), x < 1. Rfog = R. �

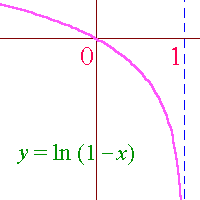R_f = R, D_g = (-�, 1),
\� R_f � D_g� �� gof is not a function.