 |
 |
 |
 |
 rigonometric Ratios
rigonometric Ratios
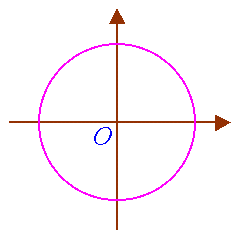
| The diagram shows a circle of radius r with its centre at the
origin.
A rotating radius OP rotates through an angle q from the x-axis. |
 |
||||||||||||
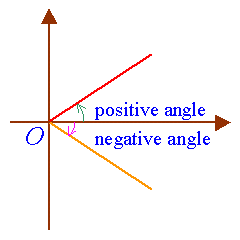
The angle q is
|
 |
||||||||||||
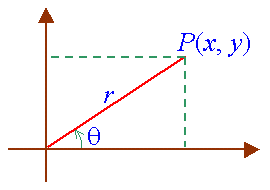
| Let (x, y) be the coordinates of the point P.� The trigonometric functions are defined as follows.
|
 |
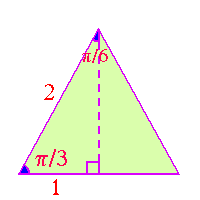
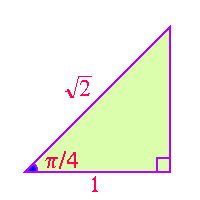
 pecial Angles
pecial Angles
|
|
|
|
|
|
|
|
|
|
|
|
|
� 2 |
� �2 |
� 2 |
|
|
|
|
|
|
|
� 2 |
� |
� 2 |
|
|
|
|
|
|
|
� �3 |
|
|
|
|
|
|
 |
 |
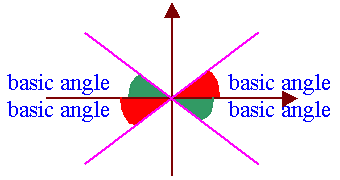
 asic Angles
asic Angles| The basic angle is the acute angle between a rotating radius and the
x-axis.
Thus 0� � basic angle � 90�. |
 |
 igns Of Trigonometric Ratios
igns Of Trigonometric RatiosIf a is the basic angle of q, then
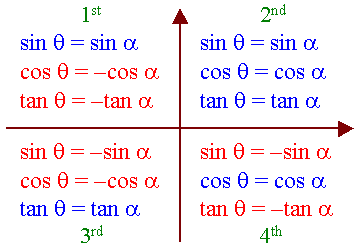
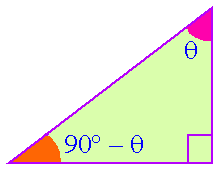
 omplementary Angles
omplementary Angles| If the sum of two acute angle is 90�,
they are said to be complementary angles of each other.
In general, for any angle q,
|
 |
 raphs Of Trigonometric Functions
raphs Of Trigonometric FunctionsThe graphs of sin x, cos x and tan x should be memorised.� Other trigonometric graphs may be generated from them by translations, scalings, reciprocal or a mixture of these transformations.
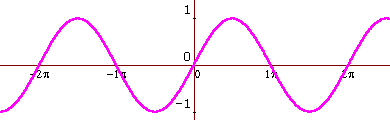
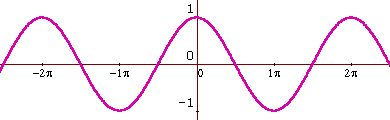
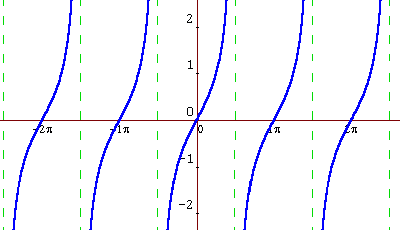
 To Other Sites
To Other Sites