 |
 |
 |
 |
 efinition
efinitionThe absolute value or modulus of a real number x, written |x| is defined as
| |x| = | ì
í î |
x
-x |
if x ³ 0,
if x < 0 (or £ 0). |
The graph of y = |x| is shown below.
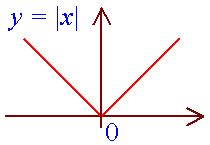
Geometrically, |x| is the distance of x from the origin.
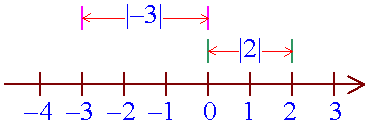
Example 1:
|
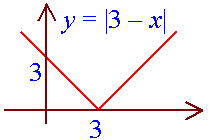
|
 roperties
roperties
 raphs of Functions Involving Modulus
raphs of Functions Involving Modulus
| Since |f(x)| = | ì
í î |
f(x)
-f(x) |
if f(x) ³ 0,
if f(x) < 0; |
the graph of y = |f(x)| is obtained from the graph of y = f(x) by reflecting the negative part (ie below the x-axis) about the x-axis.
Example 2: Sketch y = |x2 - 1|.
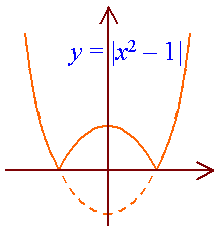
Example 3: Sketch y = |x| + |2x - 3|.
|
Example 6 will make use of this graph. |
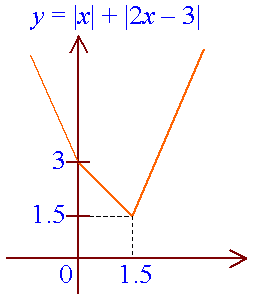
|
 nequalities Involving Modulus
nequalities Involving ModulusExample 4: Solve |3x - 2| < 3 - 2x.
Solution:
|
First of all, we must have
Next, we 'removed the modulus sign' |
||||||
|
|
||||||
| Þ 3x - 2 | < | 3 - 2x | and | 3x - 2 | > | -(3 - 2x) |
|
x
|
< | 1 |
|
x
|
> | -1 |
|
|
||||||
|
Taking the intersection, we have |
||||||
Example 5: Solve |3x - 2| > |3 - 2x|.
Solution:
| 9x2 - 12x + 4 | > | 9 - 12x + 4x2 |
|
x2
|
> | 1 |
|
|x|
|
> | 1 |
|
|
||
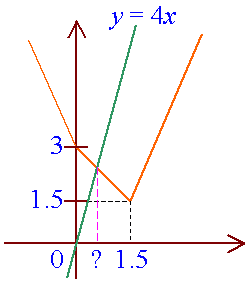
Example 6: Find the solution set of |x| + |2x - 3| ³ 4x.
Solution:
| We have sketch the graph in Example 3.
We will sketch an addition graph of y = 4x. At the point of intersection,
The solution set is {x Î R : x £ 3/5}. |
|
| Example 7: Solve |
¾¾¾ |x| - 1 |
< 3. |
Solution:
|
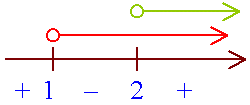
|
|||||||||||||||||||||||||
 to Other Sites
to Other Sites