Some Important Properties Solving An Inequality Interval Notation & Set-builder Notation Quadratic Inequalities Factorisable Not Factorisable Other Orders Miscellaneous Related Topics Links to Other Sites

ome Important Properties

1. Let a < b.
1. If n > 0, then

na < nb,

a/n < b/n,

an < bn (if a, b > 0).

2. If n < 0, then

na > nb,

a/n > b/n,

an > bn (if a, b > 0).

2. 1. ab > 0  Û  (a > 0 and b > 0)  or  (a < 0 and b < 0)
   2. ab < 0  Û  (a > 0 and b < 0)  or  (a < 0 and b > 0)

olving An Inequalitiy

Solving an inequality in one real variable means to find (the set of) all real values which satisfy the given inequality.

Some points to take note when solving an inequality.

1. Never cross-multiply (unless you know that all are non-negative).
2. Make one side of the inequality to zero.
3. Simplify and factorise as far as possible into linear factors.
4. For quadratic factors which are cannot be or difficult to factorise, use completing square.
5. Non-negative factors should be ignored.  Eg: x⁴, 2x² + 3, (x + 2)², (x - 1)² + 5, or even positive constants.
6. Find all the critical values where the factors are zero.
7. Use number line or graph to determine the solution.
8. The solution must not include values which make the denominators of the original inequality zero.
9. Answer must be given in set notation or interval notation when the solution set is asked for.

nterval Notation & Set-builder Notation

uadratic Inequalities

1  Factorisable

Example 1:  Find the solution set of  x² - 6x + 8 > 0.

Solution:

Factorising, (x - 2)(x - 4) > 0.

Graphically:

\  x < 2 or x > 4. The solution set is {x Î R : x < 2 or x > 4}

Number line:

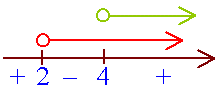\  x < 2 or x > 4. The solution set is {x Î R : x < 2 or x > 4}

Example 2:  Find the solution set of  (2x - 1)(x + 2) < x(4 + x).

Solution:

\ -1 < x < 2. The solution set is {x Î R : -1 < x < 2}

2  Not Factorisable

Example 3:  Solve x² - 4x + 1 > 0.

Solution:

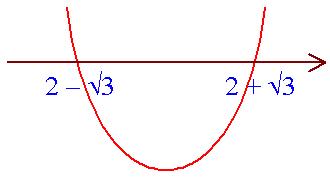\ for x2 - 4x + 1 > 0, we have x > 2 + Ö3 or x < 2 - Ö3.

Example 4:  Solve x² + 2x + 2 < 0.

Solution:

By completing square, (x + 1)² + 1 < 0.
But (x + 1)² + 1 > 1 for all real values of x.
Hence there are no real solution.
The solution set is Æ (the empty set).

Example 5:  Solve x² + 2x + 2 > 0.

Solution:

By completing square, (x + 1)² + 1 > 0.
But (x + 1)² + 1 > 1 for all real values of x.
Hence the inequality is always true for any real values of x.
The solution set is R (the set of all real numbers).

ther Orders

Example 6:  Find the solution set of  (x + 3)(x - 1)(x - 2) ³ 0.

Solution:

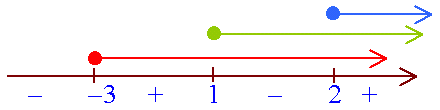\  -3 £ x £ 1  or x ³ 2. The solution set is {x Î R : -3 £ x £ 1  or x ³ 2}

Example 7:  Solve x²(x² - 1) ³ 0.

Solution:

Example 8:  Solve

(x + 2)(2x - 5) ¾¾¾¾¾¾ x - 3

³

0.

Solution:

Note that x ¹ 3. \ -2 £ x £ 5/2  or  x > 3.

Example 9:  Solve

x + 1 ¾¾¾ x - 1

£

6 ¾ x

.

Solution:

x + 1 6 ¾¾  -  ¾ x - 1 x  £  0   x(x + 1) - 6(x - 1) ¾¾¾¾¾¾¾¾ x(x - 1)  £  0   (x - 2)(x - 3) ¾¾¾¾¾¾ x(x - 1)  £  0

Note that x ¹ 0, 1. \  0 < x < 1 or 2 £ x £ 3.

iscellaneous

Example 10:  Find the values of x for which the following expression is a real number.

Solution:

Example 11:  Find the solution set of

Solution:

to Other Sites

• Inequalities
• Graphing Methods for Solving Inequalities
• S.O.S. MATHematics - Inequalities
  • Basic Rules
  • The Real Number Line, Interval Notation and Set Notation
  • Solving Polynomial Inequalities by Graphing
  • Solving Polynomial Inequalities Analytically
  • Solving Rational Inequalities Analytically