The thesis of efficiency and optimality of Indian agricultural system has several facets that have called for attention of a number of scholars. Some have proved (Rudra, 1982) allocative optimality of resource utilization, others have proved optimality of distribution of gains from agriculture, while still others have come up with the cases of marketing optimality. However, a review of the available literature reveals that regarding the thesis of marketing optimality, there is hardly any work that studies location optimality of market centers in any region of India. An elaborate survey of studies on the geography of markets carried out by Dixit (1984) may be a basis to conclude that so far no study has addressed to this aspect of the problem. In passing it may be stated that the studies that compare some existing market locations with those hypothetical ones following the n-k principle of Christaller (1933) are no studies related with the question of location optimality. Rather, they are the studies that test whether the n-k principle has any empirical validity or not. We take up, therefore, the issue of location optimality of market centers as the main theme of this paper. We pose the question: are agricultural markets location-optimal? And in the process of answering, carry out a case study of Gaya district, Bihar.
The district of Gaya, Bihar, comprises forty-six Development Blocks. Among these Blocks, eight have developed a substantially large market center located at their cores. One may note that these market centers grew up spontaneously and claimed for themselves to be declared as regulated markets at a later stage. Among these markets, the center at Gaya (Block proper) shares the largest proportion of the total market arrival of agricultural commodities while Jahanabad market shares the second largest proportion. The rest of the market centers, six in number, share varying proportions of the bulk, roughly 35-40% of the total market arrival. These percentages pertain to the average bulk of market arrivals of five major agricultural products (rice, wheat, maize, gram and potato) during 1979-82. It does not imply, however, that there are no other market centers in the district. There are indeed numerous small market centers - daily or periodic in nature (Kumar, 1983). But we restrict the scope of our investigation to the eight major (regulated) market centers only. This is so partly on account of operational reasons and partly because we believe that for optimality analysis we require a particular scale of operation, which is guaranteed at the level selected by us.
First, we take up to define location optimality. We envisage that there exists a set of points, S* , in the geographical space, such that no other set of points, say S (S ≠ S*), would characterize:
-
(a) A minimal cost of transportation of the bulk of merchandise, Xij from the origin i (i = 1, 2, ..., n) to destination j that belongs to J (J being the index set of the points in S, or alternatively, S* ), and
-
(b) A minimal cost of locating a market center of a particular type on j; (j being an element of J)
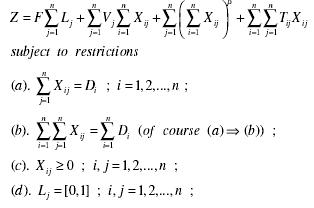
-
F = fixed cost of locating a market center. It is constant for any and every market located in any block and designed for any size of merchandise to handle,
-
Vj = per-unit variable cost of handling the merchandise at the market center, j
-
Xij = bulk of arrival of merchandise originating from block i and arriving at market location, j
-
β = the parameter representing the scale of economies emerging due to enlarged size of a market. The value of β is a positive fraction (0 < β < 1) applied as an exponent on cost or bulk
-
Tij = cost of transportation of a unit bulk from block i to market j
-
Di = total disposal of (market surplus) merchandise from block i
-
Lj = a dummy variable, taking on a value of unity (= 1) if a market center is decidedly located at block j, zero (= 0) otherwise.
We must explicitly state the assumptions underlying our definition of location optimality, partly because our model elaborated above has been developed accordingly and partly because it would help us to evaluate our approach and findings vis-à-vis other ones developed on a different concept of optimality (e.g. a la Christaller).
-
Markets may be located at any one, some or all blocks, i.e. the number of markets to be located may vary from 1 to n (n being the number of blocks, in this study n = 46).
-
The minimum number of markets located in any block i will be zero and the maximum number will be one - that is to say that not more than one market will be located in any one block. Though implied in theory and operation both, we must explicitly mention that no fractional market centers can be located. Further, the restriction of the maximum number, one, is a priori optimal, since incurring of F and scale economies at the market center precludes location of the second market center (also refer to the assumptions made latter).
-
There is no capacity ceiling on the market size, or in other words, the whole bulk of the regional (system) merchandise might arrive at a single market center, or it might be distributed among several market centers in any feasible manner.
-
The bulk of merchandise would be transported from the blocks to the market centers by the least transportation route. This might be taken as an assumption regarding the behaviour of the farmers or suppliers (Zipf, 1949).
-
Per unit cost of transportation is a linear function of the route length.
-
Market locations give rise to a fixed cost component and this is same for any and every location. This cost has no relation with the bulk size also.
-
In handling the merchandise at the market centers, there arises a variable cost component that linearly varies with the bulk of merchandise.
-
Larger the markets, greater are the economies of scale arising due to indivisibility in the facilities provided for at the site of marketing operations.
-
The market locations and capacity allocations must be such that the total system cost of marketing is minimized.
-
Supply of merchandise from each and every block must be accommodated by the markets in the region (system).
In the assumptions made above, linearity of transportation cost and handling cost is meant for simplification. We have also assumed (though tacitly) that every supplier uses the equi-cost mode of transportation. Again, this is meant for simplification. Sameness of the fixed cost of location too serves the same purpose. The last one among the assumptions attributes closedness to the region (system). However, these assumptions are not necessary for defining optimality of location in our framework. Suitable mathematical reorientation is tenable in case we drop or alter some of the assumptions. Yet, our assumptions as elaborately stated above are far more realistic than those of Christaller (1933) and others.
Given the bulk of disposal of the merchandise from each block, Di (i = 1,2,...,n) and the transportation cost matrix (Tij) along with the values of parameters like Vi, F and β, it would be possible to determine the number and locations of market centers and also to allocate the bulk of merchandise to them. The solution would give us the set S*. Now, we compare S* with S, the latter being the existing (empirical) location set. If S* is very close to S, we may conclude that S is near-optimal.
Further, we may devise a measure of near-optimality. Let C* be the system cost associated with S* and C be the system cost associated with S. Then, defining the measure, δ = (C/C* - 1) = [(C-C*)/C*], we observe that if C* = C, δ = 0, otherwise δ > 0 since C* ≤ C. The measure, δ, may be used for all intra-system arithmetic. However, we do not suggest its use for inter-system arithmetic (comparisons).
In the present study we have taken the cost of handling the merchandise (in the market) to be fixed at Rs. 2.50 per quintal. Moreover, this is constant for all markets. Further, we have assumed β = 0.5, because we have envisaged that the scale economies are quadratic in nature. The cost of transportation per quintal/mil is fixed at Rs. 0.40 which multiplied by the route length (measured from the route map, Gaya distict, forming a 46 x 46 matrix) gives us the transportation cost matrix, Tij. The least cost route from each block to all other blocks have been obtained by Shimbel's iterative algorithm for finding the least cost routes. Here we may note that all the values of parameters except that of β are based on real data, collected by the first author. The bulk of disposal or marketed surplus in each block is estimated from the secondary data on the relevant variables (Kumar & Mishra, 1985).
We have formulated the location-allocation problem in accordance with the methodology elaborated above and solved it for the gross merchandise (the total of all crops, i.e. rice, wheat, maize, gram and potato). Though we could have solved the problem for each crop separately, we preferred to deal with the total bulk due to operational reasons. We have envisaged that at no time the market will be receiving the bulk, which exceeds 20% of the annual total arrival. This assumption is based on our observations regarding the nature of market arrivals of different commodities at monthly disaggregate level. We have also observed that arrivals of individual crops match their peaks and troughs in such a way that the gross arrival in the market is better predictable than the arrival of individual crops. Moreover, market design is more dependent on the volume of mercandize than any crop specification.
The solution of the problem has been obtained by a heuristic algorithm for location-allocation devised by J K Drysdale and P J Stanford. The computer program of this algorithm is available in Ruston et al. (1973). The second author for suiting the current purpose has however, drastically modified the program. The program has been run at the Computer Center, IIT, Kharagpur.
We have observed a series of solutions for different levels of fixed cost, F, set at levels of Rs. 1.2 lakh to Rs. 2.0 lakh, at an interval of Rs. 0.2 lakh. We represent our results in the tables 1 through 3 below.
| Sl No. | Market at the Block | % of the Regional Bulk | No. of Blocks served |
| 1 | Bodh Gaya | 13.55 | 5 |
| 2 | Mohanpur | 7.77 | 3 |
| 3 | Atri | 7.34 | 4 |
| 4 | Wazirganj | 3.64 | 1 |
| 5 | Imamganj | 5.25 | 3 |
| 6 | Karpi | 6.93 | 4 |
| 7 | Ghosi | 4.50 | 3 |
| 8 | Nawada | 18.09 | 10 |
| 9 | Aurangabad | 11.08 | 4 |
| 10 | Daudnagar | 7.79 | 3 |
| 11 | Rafiganj | 8.94 | 4 |
| 12 | Madanpur | 5.30 | 2 |
| Total | Regional bulk = 528680 tonnes | 100.00 | 46 |
| Sl No. | Market at the Block | % of the Regional Bulk | No. of Blocks served |
| 1 | Bodh Gaya | 15.32 | 6 |
| 2 | Mohanpur | 11.41 | 4 |
| 3 | Atri | 10.64 | 6 |
| 4 | Imamganj | 5.25 | 3 |
| 5 | Karpi | 14.06 | 8 |
| 6 | Nawada | 18.09 | 10 |
| 7 | Aurangabad | 25.22 | 9 |
| Total | Regional bulk = 528680 tonnes | 100.00 | 46 |
| Sl No. | Market at the Block | % of the Regional Bulk | No. of Blocks served |
| 1 | Manpur | 32.03 | 14 |
| 2 | Mohanpur | 7.76 | 3 |
| 3 | Imamganj | 7.60 | 4 |
| 4 | Karpi | 12.18 | 7 |
| 5 | Nawada | 18.09 | 10 |
| 6 | Aurangabad | 22.33 | 8 |
| Total | Regional bulk = 528680 tonnes | 100.00 | 46 |
Of the three tables presented above, the table #3 (F = Rs. 1.6 lakh) represents a stable solution. Other two tables may be referred to for observing the impact of changes in the levels of fixed cost for market location, but they are not final. For finality, we take the results presented in table # 3 (for F = Rs. 1.6 lakh).
A comparison of the results obtained from this exercise with the existing market locations and arrivals of merchandise at them reveals that the former has a tendency to coincide with the latter. However, the locations of the markets in the two profiles (namely the existing and the optimal) are evidently different. Manpur* (the superscript * denotes the location obtained by optimality search) is is contiguous to Bodh Gaya, Mohanpur* is contiguous to Sherghati, Karpi* is contiguous to Arwal and Daudnagar, while Nawada* and Aurangabad* are already the existing markets. Thus, out of the six markets selected by the optimality criterion, four are contiguous and adjacent to the existing ones and the rest are identical to the existing ones.
The existing market center at Warisaliganj has been ignored by the optimality search probably in favour of selecting Nawada* with a larger volume of allocation. Arwal has been ignored due to loaded favour (larger volume of allocation) made to Karpi*. Jahanabad has been rather rudely ignored, maybe due to openness of the region towards Patna, while a new location in the Block of Imamganj* has been favoured with a marked trace of preference (refer to persistence of its selection in all the tables). It appears that Jahanabad is located at a cost-inpotimal site and, might be due to the same reason, it has a tendency to lose its share in the regional merchandise which has been observed by us while analysing the trends in the shares of the merchandise commanded by different markets (Kumar, 1983).
Our findings may lead one to believe that existing market locations and arrivals of merchandise at them are very close to what might have been if they had been located on the principle of optimality. It is reflected in the value of the measure, δ = 0.1139, which may be considered to be very close to zero. This conjecture is quite legitimate if we note that the existing markets have developed in an open region, unlike our cost-optimal locations searched out in a closed region (closedness is a consequence of our model). Hence a discount must be made in favour of the existing locations, and we do not have enough reasons and evidence to conclude that the existing markets are inoptimally located. Thus, we answer our question (raised at the outset) in affirmative and assert that the existing agricultural markets in Gaya district are location-optimal.
Nevertheless, cost-optimality is only a condition for location, growth, potentiality and size of the market centers and this condition is not all and every thing, sufficient to justify locations. Many other factors are at work behind location and growth of markets. The cost-optimality criterion may be used only as a modest and simplified attempt to analyze the forces of location, size and growth of market centers.
1. Christaller, W (1933) The Central Places of Southern Germany (translated by C Baskin (1965), Prentice Hall, Englewood Cliffs, NJ.
2. Dixit, RS (1984) Market Centres and their Spatial Development in the Umland of Kanpur, Kitab Mahal, Allahabad.
3. Kumar, Binod (1983) Regional Planning Approach to an Efficient Agricultural Marketing System, (unpub) MRP Dissertation, Dept. of Arch & Regional Planning, IIT, Kharagpur.
4. Kumar, Binod and SK Mishra (1985) "Determinants of Regional Marketed Surplus of Agricultural Commodities : A Case Study of Gaya District, Bihar" NEHU Journal of Social Sciences and Humanities, Vol III (3), 61-64.download
5. Rudra, Ashok (1982) Indian Agricultural Economics : Myths and Realities, Allied, New Delhi.
6. Ruston, G, MF Goodchild and LM Ostresh, Jr. (1973) Computer Programs for Location-Allocation Problems, Monograph No. 6, Dept. of Geography, Univ. of Iowa, Iowa.
7. Zipf, GK (1949) Human Behaviour and the Principles of Least Effort, A Wasley Press, Cambridge.