Kim. Yük. Müh. Kadir VATANSEVER
1. GİRİŞ
Mühendislik alanında karşılaşılan önemli sorunlardan birisi sayısal çözümlerin verdiği sonuçların probleme uymamasıdır. Böylece çözümü var olan bir problem çözümsüz olarak kalmaktadır. Bu durum bir çok değişkenin ve verinin söz konusu olduğu hemen hemen tüm sayısal çözümlerde kendini göstermektedir.
Çok sayıda değişkenin olduğu lineer denklem sistemleri bunun için bariz bir örnektir. Bu sistemlerin çözümünde karşılaşılan zorlukların aşılmasında ve doğru sonuçların elde edilmesinde Holotransformasyon etkili bir yöntem olarak ortaya çıkmaktadır. E. Büyükkoca tarafından geliştirilen yöntemin verdiği sonuçların hassasiyeti ve doğruluğu kendisinin daha önceki çalışmalarında gösterilmiştir. [11,12,13]
Bu yüzden kesikli distilasyon bu açıdan ele alınmış ve integral denklemler kesikli distilasyon hesaplamalarında denenmiştir. İntegral denklemler bir çok fiziksel halin anlatılmasında en uygun ifadelerdir. İntegral denklemlerin sayısal çözümleri lineer denklem takımları halinde yapılmaktadır. Bu denklem takımlarının çözümü çoğu kez problemin sonuçlarına uymamaktadır. Bu durum, hassasiyetin arttırılması amacıyla aralık sayısının arttırılmasından ileri gelir. Ancak Holotransformasyon, böyle sistemlerin çözümünde dahi uygun sonuçlar vermektedir.
2. KESİKLİ DİSTİLASYON
Sürekli distilasyon, distillenecek madde bol miktarda bulunduğunda, makul sabit bir hızda ayırma için uygundur. Bu şartlar altında, çoğunlukla kesikli distilasyondan daha ucuzdur. Ancak sürekli işleme uygun olmayan ve kesikli temelinde ele alınan çok sayıda durum söz konusudur.
Bir kesikli distilasyon, saflaştırma kolonu ile dolum kazanı gerektirir, ayrılacak madde ile istenilen miktar distilleninceye kadar ayırma işlemine devam edilir. Tepe ürünü bileşimi ayırma işlemi esnasında değişecektir. Kesikli distilasyon kolonlarının çalışmaları sürekli distilasyon kolonlarıyla benzerlik göstermesine rağmen hesaplamalarda bu böyle olmamaktadır. Sürekli distilasyon kolonlarının tüm kısımlarında akış hızları ve bileşimler zamandan bağımsızdır. Bu şartlar kesikli distilasyona uygulanamamakta, sürekli değişimlerden dolayı diferansiyel olarak incelenmektedir. Sonuç olarak hesaplamalar oldukça zorlaşmakta ve bir kaç basit hal için hesaplama yöntemleri geliştirilmiştir.
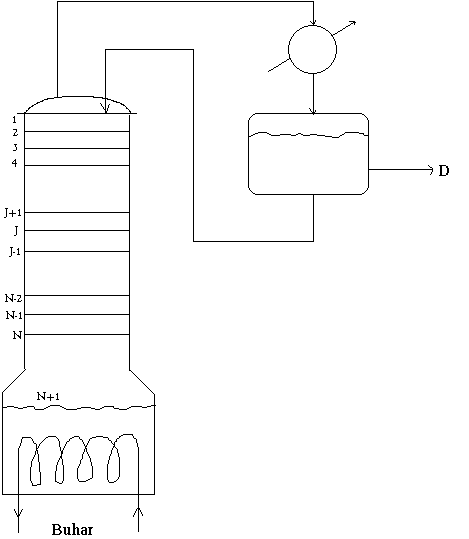
Şekil 1: Kesikli distilasyon kolonu
3. HESAPLAMA YÖNTEMLERİ
3.1. Kolon İçinde Sıvı Birikmesinin Olmadığı Durumda Saflaştırma
3.1.1. Sınırlı Riflaks Oranı
En eski yöntemlerden biri Rayleigh denklemi ile aynı bir bağıntı kullanan Smooker ve Rose tarafından önerilmiştir. Burada, raflarda tutulan sıvı ihmal edilmektedir. Bu denklemin bir çıkarılışı şu şekildedir; Kolon ayırma işlemine başladıktan sonra herhangi bir zamanda i bileşeni için kütle denkliği oluşturalım. Distilat akımının zaman içindeki değişimi sürekli azalma yönünde olacaktır. (tn) anından (tn+D t) anına kadar distilatta ortaya çıkan di akımı kazandaki azalmaya denk düşer. O halde;
![]()
yazılabilir. Distilasyon kolonu ayrım yapacak hale geldikten sonra (t=0) Di ve Li 'nin zamana bağlı değişimleri Şekil 1 ve Şekil 2 'deki gibi olur.
Di eğrisi için t ekseni asimptot olurken Li eğrisi için de L
doğrusu asimptot olmaktadır. Çünkü ![]() olurken
olurken ![]() ve Li ®
L limit değerlerine yaklaşır. Bu sınır şartlarından da anlaşılacağı gibi, Li
'nin zamana bağlı diferansiyel değişimleri Di akımının anlık akış hızlarına
eşit olur. Dolayısıyla (1) denklemi,
ve Li ®
L limit değerlerine yaklaşır. Bu sınır şartlarından da anlaşılacağı gibi, Li
'nin zamana bağlı diferansiyel değişimleri Di akımının anlık akış hızlarına
eşit olur. Dolayısıyla (1) denklemi,
![]()
haline dönüşmektedir. Aynı zamanda bu denklem,
![]() şeklinde yazılabilir.
şeklinde yazılabilir.
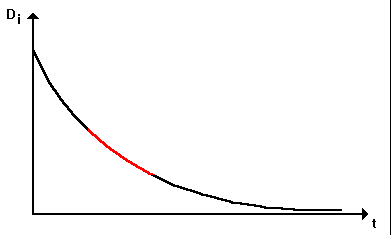
Şekil 2: Distilat akımının zamana bağlı değişimi
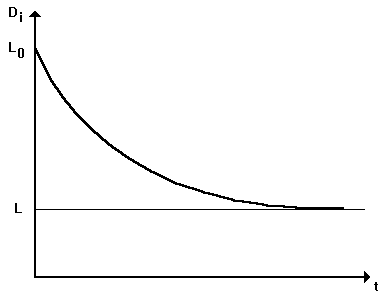
Şekil 3: Kaynatıcıdaki madde miktarının zamana bağlı değişimi
Bu kesikli distilasyon kolonunda toplam madde dengesi için,
![]()
denklemi yazılabilir. (3) denklemi açık olarak yazılır ve (4) denklemi ile kombine edilirse;


denklemi elde edilir.
Bu Rayleigh denklemi olarak bilinir ve bu denklemin integrasyonu için XD,i ve XN+1,i değerleri arasındaki değişimin nasıl olduğunun bilinmesine ihtiyaç vardır. Rayleigh denklemi aşağıdaki gibi sade bir biçimde yazılabilir:
![]()
Raflar üzerinde sıvı birikmesinin olmaması, herhangi bir raf üzerinde sıvı ve buhar akımlarının dengede olduğunu gösterir. Öyleyse kesikli distilasyon kolonunun çalışması esnasında herhangi bir zamanda n. ve (n+1). raflar arasındaki madde denkliği ile elde edilecek operasyon doğrusu, sürekli distilasyondaki gibi olacaktır. Bu durumda operasyon doğrusu,
![]()
olur.
Bu doğrunun ard arda uygulanmasıyla (XL-XD) değerleri XL 'nin bir fonksiyonu olarak elde edilebilmekte ve (9) denkelminin integrasyonu yapılabilmektedir. Böyle bir distilasyon hesaplamaları bir kaç yolla yapılabilir. Çok bilinen iki yöntem; distilasyon işleminin sabit riflaks oranıyla yapılarak istnilen bileşim ortalama olarak veya değişken riflaks oranlarıyla istenilen bileşimin elde edilmesidir.
Sabit geri dönüş oranı olması halinde (10) doğrusunun eğimi (On+1/Vn) sabit kalır. XL 'nin çeşitli değerleri için bu eğime sahip bir seri operasyon doğrusunun üzerinde teorik raf sayısına eşdeğer sayıda adım olacak şekilde çizilmesiyle XD değerleri tespit edilir. Böyle bir işlem Şekil 4 'te gösterilmektedir. Bu şekilde ln(L0/L) değeri çeşitli nümerik yollarla bulunarak alt ve üst akımların bileşimleri ve miktarları bulunmuş olur.
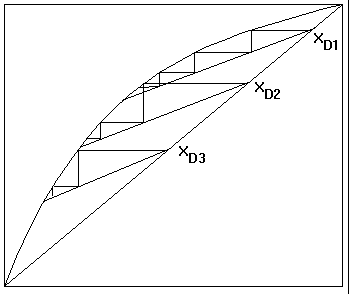
İkinci durumda XD 'nin değeri sabittir. Bu durum, değişen riflaks oranlarıyla sağlanmaktadır. XL 'nin değişen değerleri için çizilen farklı eğimlerde operasyon doğruları XD noktasında kesişirler. Bu durum Şekil 5 'te gösterilmiştir. Böyle bir işlem sayesinde (9) denklemi üst akım miktarı ve kazanda kalan sıvının bileşimi arasındaki bir bağıntı yardımıyla integre edilmektedir. Değişken geri dönüş oranı için kullanılan bağıntı şu şekilde bulunabilir;
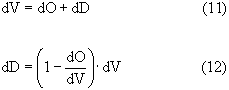
ve kütle dengesi yardımıyla,
![]()
Şekil 4: Sabit geri dönüş oranı durumunda operasyon doğruları
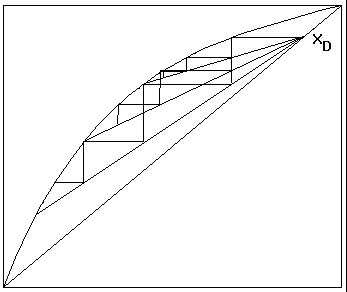
Şekil 5: Sabit distilat bileşimi durumunda farklı eğimlerde operasyon doğruları
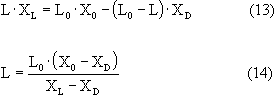
Elde edilen bu denklem (9) denkleminde yerine konursa ;
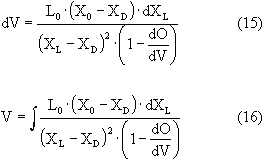
elde edilir. Şekil 5 'te XD 'den geçen farklı eğimlere sahip bir seri operasyon doğrusunun üzerinde raf sayısına denk gelecek şekilde XL değerlerinin tespiti ile (16) denkleminin integrasyonu mümkün olabilmektedir.
3.1.2. Tam Geri Dönüş Oranı
Limit şartların kesikli distilasyon için hesaplanması çeşitli
amaçlar için faydalıdır. Tam riflaks limiti sabit geri dönüş kategorisine girer.
Tam geri dönüş oranı istenilen saflaştırmayı minimum raf sayısıyla
sağlamaktadır. Kaynatıcı dahil (N+1) raf sayısı için ikili bir (A+B)
karışımında izafi uçuculuk sabit olduğunda aşağıdaki denklemler geçerlidir:
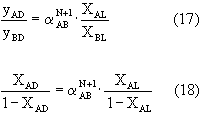
(18) denklemi kullandığımız değişkenlere uygun olması bakımından;
![]()
şeklinde yazılabilir.
![]()
Elde edilen bu denklem (9) denkleminde yerine konulur ve elde edilen denklem X0, L0 'dan X,L değerlerine interge edilirse;
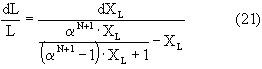
![]()
elde edilmiş olur. Ancak bu son denklem sabit uçuculuk için geçerli olmaktadır. Eğer bağıl uçuculuk sabit değilse y=f(x) denge eğrisi ile operasyon doğrularının yardımıyla elde edilen grafikten faydalanarak XL 'nin çeşitli değerleri için XD değerleri bulunarak sayısal integral alınır.
3.1.3. Minimum Buhar Gereksinimi
Minimum buhar gereksinimi, distilasyon için bir başka limit şarttır. Bu durum sürekli distilasyonlarda minimum riflaks oranı şartına uyar. Bu durumda gerekli teorik raf sayısı sonsuzdur. Zira, operasyon doğrusu denge eğrisini bir noktada kesmektedir. Böylece grafik olarak sabit yada değişen riflaks oranları için XD, XL 'nin bir fonksiyonu olarak yada (dO/dV) eğimi tespit edilerek (9) ve (16) denklemleri integre edilebilmektedir.
Uçuculuğun sabit kalması durumunda analitik bir çözüm mümkün olmaktadır. Bunun için sabit riflaks durumunu gözönüne alalım. Böyle bir durumda operasyon çizgisi denge eğrisini XD=1 ve X=XL' noktalarında kesecektir. XD=1 'den daha düşük değerlerde kesim noktası XL olacaktır.
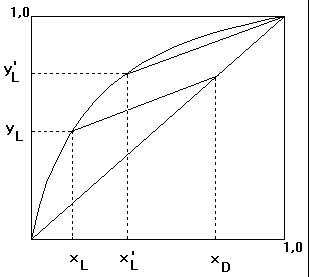
Şekil 6: Minimum buhar gereksinimi durumunda operasyon doğruları
![]()
Buna göre sabit bağıl uçuculuk için,
![]()
elde edilir. Aynı zamanda XL' 'den daha düşük olduğu durumlar için;
![]()
denklemi yazılabilir. Sabit uçuculuk göz önünde bulundurularak;
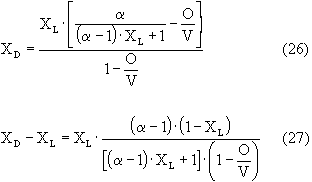
elde edilen bu son denklem, (9) denkleminde yerine konulur ve XL' , L' 'den XL ve L değerlerine integre edilirse;

denklemi ele geçer.
3.2. Kolonda Sıvı Tutulmasıyla Saflaştırma
Sürekli distilasyon kolonlarında raflarda tutulan sıvı hesaplamalarda herhangi bir güçlük ortaya çıkarmaz. Hatta raflar üstünde denge kurulmasında ve ayrılmanın sağlanmasında önemli ölçüde bir fayda sağlamaktadır. Raflarda tutulan sıvının kesikli distilasyonda kolona olan etkisi tam anlamıyla açık değildir. Çünkü bu işlemi tam olarak analiz eden bir yöntem geliştirilememiştir. Yine de bu durumda kesikli distilasyon için ayrıntılı bir diferansiyel integrasyon yapılabilmektedir. Ancak, bu yönde yapılan çalışmalar elde edilen sonuçları haklı çıkarmamaktadır. Yine de bu yöntem kolonda tutulan sıvı miktarı göz önünde tutularak kesikli distilasyonun incelenmesinde ve kurallarının geliştirilmesinde faydalıdır. Daha önceden elde edilen (9) denklemine benzer şekilde kolonda tutulan sıvı miktarı H ve her raf üzerindeki sıvıların ortalama bileşimi XH olmak üzere;
![]()
yazılabilir. Bu denklemin integrasyonu için (H.XH) ile L ve XL arasındaki bağıntının bilinmesine ihtiyaç duyulmaktadır. Bu bağıntı oldukça karmaşık ve doğrudan integrasyon için uygun bir halde ifade edilememektedir. Bu denklemi basitleştirmek için H sabit kabul edilir.
Bir raf üstünde madde denkliği göz önüne alınarak operasyon doğrusu şu şeklide yazılabilir:
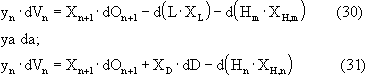
Burada HmXH,m ve HnXH,n kazanda ve raflarda tutulan tün sıvı bileşimine eşittir. Bu denklemlerdeki son terimler d(HmXH,m) ve d(HnXH,n) her bir rafta değiştiği için operasyon çizgisi bir eğridir. Tam riflaks olması halinde bu terimler ihmal edilebilmekte ve operasyon çizgisi diagonal olmaktadır. Böylece işlem daha önceden gösterilen sıvı tutulmasının olmadığı duruma dönüşmüş olur. Ancak sınırlı bir geri dönüş oranı için operasyon çizgisi bir eğridir ve değişimlerin elde edilmesi güçtür.
Kesikli distilasyon değişen riflaks oranlarında sabit XD değerinde çalışırken distilasyon, riflaks oranı toplam riflaks oranı oluncaya kadar devam etmektedir. Böylece distilasyon sonunda köşegen üzerinde çakışan operasyon çizgisi yardımıyla raflarda tutulan sıvının bileşimi kolaylıkla bulunabilir. (Bu konuda daha ayrıntılı bilgi için Ref. 1 'e bakınız.)
4. KESİKLİ DİSTİLASYON KOLONLARININ HESAPLANMASINDA
SAYISAL ÇÖZÜMLER
Mühendislikte genel olarak birbirine paralel ve birbiriyle ilişkileri bulunan iki çözüm yolu vardır. Bunlardan birincisi deneysel, diğeri teorik çalışmalardır. Deney sonuçları çoğu kez tablolar halinde verilen kesikli sayısal değerlerdir. Teorik çalışma sonuçları sürekli değerler olduğu halde deney sonuçları ile karşılaştırılması amacıyla kesikli değerler halinde sayısal olarak ifade edilirler. Deneyler ile karşılaştırılmak istenilen bir problemin teorik çözümü, bu karşılaştırmayı yapabilecek bir çözümün yetersiz olması yada hiç çözüme sahip olmaması nedeniyle olanaksız hale gelmektedir. Kısacası teorik çözüm yolu elverişli olmamaktadır. O zaman problemi demneylerle çözmek, kesikli değerler elde etmek yararlı olur. Deneylerle bulunan sonuçları değerlendirmek veya böyle bir problemi hiç deney gereği olmadan kesikli değerler halinde vermek mümkündür. İşte böyle bir yola sayısal yöntem yada sayısal analiz denir. Bütün bunların dışında daha önceden elde edilen (9) denklemi için sayısal yöntemler ve çözüm yöntemleri daha önceden verilen literatüre geçmiş bir problem için incelenecektir.
4.1. Bir Kesikli Distilasyon Problemi İçin Sayısal Çözümler
Alternatif çözüm yöntemi önerilmeden önce klasik yöntemlerle çözülmüş bir problem çözüm tekniklerinin incelenmesi bakımından aynı şekilde yeniden ele alınmıştır. [3]
A ve B bileşenlerinin karışımından meydana gelmiş ikili bir sistem, 7 teorik raf sayısına ve R=2.5 geri dönüş oranına sahip bir kesikli ayırma kolonu yardımıyla saflaştırılmak isteniyor.
İzafi uçuculuk a =10-8.95X şeklinde sıvı faz bileşimine bağlı olarak ifade ediliyor. Başlangıçta kazana yüklenen karışım 100 mol ve %50 A içermektedir. Bu şartlar ile distilasyona başlanıyor. Kolon içinde raflarda sıvı birikmesinin olmadığı ve sıvı-buhar fazları için eşit molal akış hızının olduğunu kabul ediyoruz. Taban üründe en fazla %5 A bulunmasına müsaade ediliyor. Ayrılma tamamlandıktan sonra baş ve taban ürünlerin miktarlarını ve bileşimini bulalım. Bunun için elde edilen distilatı D ve kaynatıcıda kalan sıvı miktarını L ile gösterecek olursak kütle denkliklerinden;

kesikli distilasyon için diferansiyel denklem elde edilmiş olur. Bu denklem problem şartları için integre edilirse;
![]()
elde edilir. Raflarda sıvı tutulmasının ihmali ve sabit riflaks oranı bize;
![]()
denklemini yazmamıza olanak verir. Aynı zamanda denge şartları için;
![]()
denge eğrisi fonksiyonunu biliyoruz. Bu durumda XL 'nin integral aralığında değişen değerleri için grafik olarak şu değerler verilmektedir:
Tablo 1:
XL |
1/(XD-XL) |
0.05 |
1.10496829 |
0.10 |
1.15473819 |
0.15 |
1.22190530 |
0.20 |
1.29908149 |
0.25 |
1.38747509 |
0.30 |
1.48915890 |
0.35 |
1.60726079 |
0.40 |
1.74589400 |
0.45 |
1.91102239 |
0.50 |
2.11111239 |
Sayısal integral almadan önce yeterli aralık sayısı elde etmek amacıyla çeşitli polinomiyal enterpolasyon formüllerinden faydalanabiliriz. Bunun için Lagrange ve Newton ileriye fark enterpolasyon formülleri kullanılmıştır.
Lagrange Enterpolasyonu:
Lagrange enterpolasyon formülü,

y0 değeri için L0(x) özel polinomunu Tablo 1 'de verilen noktalar için;
![]()
şeklinde yazılır. Buna benzer şekilde her bir yi değeri için Li(x) özel polinomları oluşturulur. Bu şekilde;
![]()
Lagrange enterpolasyon formülü oluşturulmuş olur. Elde edilen P(x) polinom formülü ile 80 aralık için alınan sonuçlar Tablo 3 'de görülmektedir.
Newton Enterpolasyonu:
Newton ileriye fark enterpolasyon formülü şu şekildedir;
![]() Bu formülün
kullanımı için elde edilen ileriye fark değerleri Tablo 2 'de gösterilmektedir.
Bu formülün
kullanımı için elde edilen ileriye fark değerleri Tablo 2 'de gösterilmektedir.
Newton ileriye fark formülü ile elde edilen polinom için 80 aralıkta alınan sonuçlar Tablo 3 'te gösterilmektedir.
Tablo 3: Lagrange ve Newton yöntemleriyle alınan sonuçlar
Lagrange |
Newton |
||
x |
P(x) |
P(x) |
|
0.05000000 |
1.1048250925 |
1.1049682900 |
|
0.05562500 |
1.1085215160 |
1.1087179210 |
|
0.06125000 |
1.1128801971 |
1.1131422950 |
|
0.06687500 |
1.1177847760 |
1.1181261530 |
|
0.07250000 |
1.1231388072 |
1.1235741718 |
|
0.07812500 |
1.1288629742 |
1.1294081729 |
|
0.08375000 |
1.1348926111 |
1.1355646401 |
|
0.08937500 |
1.1411755067 |
1.1419925191 |
|
0.09500000 |
1.1476699672 |
1.1486512755 |
|
0.10062500 |
1.1543431151 |
1.1555091906 |
|
0.01062500 |
1.1611694047 |
1.1625418719 |
|
0.11187500 |
1.1681293323 |
1.1697309596 |
|
0.11750000 |
1.1752083248 |
1.1770630113 |
|
0.12312500 |
1.1823957872 |
1.1845285452 |
|
0.12875000 |
1.1896842944 |
1.1921212277 |
|
0.13437500 |
1.1970689111 |
1.1998371891 |
|
0.14000000 |
1.2045466253 |
1.2076744522 |
|
0.14562500 |
1.2121158834 |
1.2156324629 |
|
0.15125000 |
1.2197762137 |
1.2237117084 |
|
0.15687500 |
1.2275279266 |
1.2319134125 |
|
0.16250000 |
1.2353718826 |
1.2402392977 |
|
0.16812500 |
1.2433093173 |
1.2486914041 |
|
0.17375000 |
1.2513417147 |
1.2572719565 |
|
0.17937500 |
1.2594707222 |
1.2659832725 |
|
0.18500000 |
1.2676980981 |
1.2748277030 |
|
0.19062500 |
1.276025687 |
1.2838076002 |
|
0.19625000 |
1.2844554169 |
1.2929253058 |
|
0.20187500 |
1.2929893124 |
1.3021831562 |
|
0.20750000 |
1.3016295198 |
1.3115834982 |
|
Tablo 3: (Devamı)
Lagrange |
Newton |
||
x |
P(x) |
P(x) |
|
0.21312500 |
1.3103783413 |
1.3211287137 |
|
0.21875000 |
1.3192382732 |
1.3308212476 |
|
0.22437500 |
1.3282120474 |
1.3406636382 |
|
0.23000000 |
1.3373026722 |
1.3506585469 |
|
0.23562500 |
1.3465134722 |
1.3608087858 |
|
0.24125000 |
1.3558481243 |
1.3711173413 |
|
0.24687500 |
1.3653106909 |
1.3815873935 |
|
0.25250000 |
1.3749056475 |
1.3922223305 |
|
0.25812500 |
1.3846373069 |
1.4030257567 |
|
0.26375000 |
1.3945128370 |
1.4140014969 |
|
0.26937500 |
1.4045362765 |
1.4251535936 |
|
0.27500000 |
1.4147145429 |
1.4364863019 |
|
0.28062500 |
1.4250544444 |
1.4480040783 |
|
0.28625000 |
1.4355632808 |
1.4597115685 |
|
0.29187500 |
1.4462488499 |
1.4716135920 |
|
0.29750000 |
1.4571194509 |
1.4837151259 |
|
0.30312500 |
1.4681838895 |
1.4960212898 |
|
0.30875000 |
1.4794514852 |
1.5085373314 |
|
0.31437500 |
1.4909320818 |
1.5212686143 |
|
0.32000000 |
1.5026360627 |
1.5342206107 |
|
0.32562500 |
1.5145743715 |
1.5473988978 |
|
0.33125000 |
1.5265853950 |
1.5608091600 |
|
0.33687500 |
1.5392007198 |
1.5744571979 |
|
0.34250000 |
1.5519137301 |
1.5883489438 |
|
0.34812500 |
1.5649111027 |
1.6024904848 |
|
0.35375000 |
1.5782071445 |
1.6168880936 |
|
0.35937500 |
1.5918170032 |
1.6315482659 |
|
0.36500000 |
1.6057567433 |
1.6464777655 |
|
0.37062500 |
1.6200434278 |
1.6616836750 |
|
Tablo 3: (Devamı)
Lagrange |
Newton |
||
x |
P(x) |
P(x) |
|
0.37625000 |
1.6346952061 |
1.6771734511 |
|
0.38187500 |
1.6497314062 |
1.6929549837 |
|
0.38750000 |
1.6651726292 |
1.7090366555 |
|
0.39312500 |
1.6810408426 |
1.7254274008 |
|
0.39875000 |
1.6973594713 |
1.7421367590 |
|
0.40437500 |
1.7141534805 |
1.7591749205 |
|
0.41000000 |
1.7314494481 |
1.7765527601 |
|
0.41562500 |
1.7492756202 |
1.7942818531 |
|
0.42125000 |
1.7676619461 |
1.8123744687 |
|
0.42687500 |
1.7866400842 |
1.8308435343 |
|
0.43250000 |
1.8062433746 |
1.8497025645 |
|
0.43812500 |
1.8265067686 |
1.8689655458 |
|
0.44375000 |
1.8474667075 |
1.8886467700 |
|
0.44937500 |
1.8691609424 |
1.9087606061 |
|
0.45500000 |
1.8916282824 |
1.9293212009 |
|
0.46062500 |
1.9149082631 |
1.9503420969 |
|
0.46625000 |
1.9390407215 |
1.9718357563 |
|
0.47187500 |
1.9640652649 |
1.9938129773 |
|
0.47750000 |
1.9900206203 |
2.0162821830 |
|
0.48312500 |
2.0169438495 |
2.0392436111 |
|
0.48875000 |
2.0448694125 |
2.0627132603 |
|
0.49437500 |
2.0738280644 |
2.0866717878 |
|
0.50000000 |
2.1038455655 |
2.1111131300 |
|
Tablo 3 'teki polinom değerleri, doğruya yakın integral değerleri elde etmek amacıyla hesaplanmış ve integral hesabında Simpson ve Trapez integral kurallarından faydalanılmıştır.
Simpson kaidesine göre integral denklemi:
![]()
Trapez kaidesine göre integral denklemi:
![]()
Bu iki yönteme göre (32) denkleminin integralinin sayısal değerleri aşağıdaki tabloda sunulmaktadır.
Tablo 4:
Aralık Sayısı |
Simpson Kuralı |
Trapez Kuralı |
18 |
0.670446 |
0.670642 |
36 |
0.670446 |
0.670494 |
80 |
0.670386 |
0.670457 |
Bu iki yöntem için hata formülüyle düzeltilen değerler, Simpson kuralı için 0.670446 ve Trapez kuralı için 0.670445 şeklindedir. O halde;
![]()
L = 51.14804066 mol
Baş ürün = 100 - 51.14804066
= 48.85195934 mol
Baş üründe A'nın mol miktarı = 47.44259797 mol
Baş üründe B'nin miktarı = 1.40936137 mol olur.
Baş ürünün bileşimi XD = 0.971149875 bulunur.
5. KESİKLİ DİSTİLASYON PROBLEMİNİN İNTEGRAL DENKLEMLERLE
ÇÖZÜMÜ
Bir çok fiziksel hal integral denklemlerle kolayca ifade edilebilir. Bizim problemimizde (32) denklemi 1. çeşit Fredholm integral denklemine dönüştürülebilir. Bunun için; XD = X ve XL = t alınırsa;
![]()
yazılabilir. Burada 1/(x-t) 'nin çekirdek fonksiyon olduğu açıkça görülmektedir. Öyleyse son durumda, genel olarak;
![]()
yazılır ve bu Fredholm integral denklemlerinin birinci çeşididir.
5.1. Sayısal Çözüm İçin İntegral Denklemin Denklem Takımına Dönüştürülmesi
Tablo: 5
t |
k(x,t) |
x |
y(x) |
0.050 |
1.104968290 |
0.9550033463 |
0.6876338678 |
0.095 |
1.148651275 |
0.9655862447 |
0.6258694764 |
0.140 |
1.207674452 |
0.9680377202 |
0.5705098177 |
0.185 |
1.274827703 |
0.9694197280 |
0.5134469337 |
0.230 |
1.350658547 |
0.9703795743 |
0.4536230193 |
0.275 |
1.436486302 |
0.9711430809 |
0.3903933863 |
0.320 |
1.534220611 |
0.9717967448 |
0.3231845048 |
0.365 |
1.646477766 |
0.9723571236 |
0.2513816428 |
0.410 |
1.776552760 |
0.9728878706 |
0.1742221438 |
0.455 |
1.929321201 |
0.9733170120 |
0.0908216677 |
0.500 |
2.111113130 |
0.9736837575 |
0 |
Simpson kuralına göre (35) denkleminin integrali şu şekildedir:
![]() 5.1.1. Denklem
Takımının Klasik Yöntemlerle Çözümü
5.1.1. Denklem
Takımının Klasik Yöntemlerle Çözümü
Oluşturulan matris sistemi, mukayese amacıyla öncelikle [A][u]=[b] şeklinde çözülmüş ve aşağıdaki sonuçlar bulunmuştur:
D
= -1.468435280021942 x 10-60| D 1 = 1.757890319567805 x 10-51 | U1 = -1197118009.546555 |
| D 2 = -4.9736500539435 x 10-55 | U2 = 338704.0696726642 |
| D 3 = -8.219413194592668 x 10-52 | U3 = 559739561.3152151 |
| D 4 = 2.02873325886868 x 10-51 | U4 = -1381561234.921001 |
| D 5 = -6.201133007812155 x 10-51 | U5 = 4222952888.818835 |
| D 6 = 6.260397236605596 x 10-59 | U6 = -42.26537814804379 |
| D 7 = 3.522686702956781 x 10-52 | U7 = -239893902.7741245 |
| D 8 = 1.438490851277916 x 10-51 | U8 = -979607934.2743804 |
| D 9 = -6.555287438827502 x 10-52 | U9 = 446413098.8959588 |
| D 10 = -2.265174386864645 x 10-52 | U10 = 154257693.0479904 |
| D 11 = 1.645490018287978 x 10-55 | U11 = -112057.3743136565 |
5.1.2. Denklem Takımının Holotransformasyonla Çözümü
Holotransformasyon yönteminin çözüm tekniği; [A].[u] = [b] şeklindeki bir lineer denklem sisteminin 1. dönüşümü aşağıdaki şekilde yapılır:
![]()
![]() , yansıtılan uzayda
, yansıtılan uzayda ![]() vektörünün görüntüsüdür. Gerçek
değerlere geri dönüş,
vektörünün görüntüsüdür. Gerçek
değerlere geri dönüş,
![]()
denklemiyle sağlanmaktadır.
Bu şekilde, yukarıdaki lineer denklem sistemi için elde edilen sonuçlar aşağıdaki gibi bulunmuştur:
|
u |
|
1 |
-347554929.8685224 |
-4.91023736981424x1014 |
2 |
-6906593082.992033 |
-4.822050950004346x1014 |
3 |
1.342215510433599x1013 |
-4.801919992942785x1014 |
4 |
-5.980934114813773x1013 |
-4.785846712695237x1014 |
5 |
4.440546230691564x1013 |
-4.783153220584023x1014 |
6 |
5.604187213500787x1013 |
-4.777016742179942x1014 |
7 |
-1.464565961101045x1013 |
-4.792230764697794x1014 |
8 |
-1.077024050775165x1014 |
-4.767292067803436x1014 |
9 |
8.993868819138677x1013 |
-4.763053322878241x1014 |
10 |
-2.95679725097573x1013 |
-4.759631630968424x1014 |
11 |
7.924961131359776x1012 |
-4.756711400397215x1014 |
6. SONUÇ VE TARTIŞMA
Lapidus [3] tarafından yapılan çözümde problem sadece verilen şartlar için çözülmüşken integral denklemlerle başlangıç şartlarından bağımsız olarak genel bir çözüm elde edilmektedir. Elde edilen y(x) fonksiyonu sadece distilat akımı bileşiminin bir fonksiyonu olmaktadır. Dolayısıyla biz istediğimiz XD değerini bu fonksiyonda yerine koyarak ln(L0/L) değerini doğrudan tayin edebilmekteyiz. Bu sayede kazanda bulunan sıvının bileşiminin XD 'nin bir fonksiyonu olarak kesikli değerler halinde elde etmek mümkündür.
Ancak integral denklemlerin sayısal çözümlerinde ortaya çıkan hastalıklı sistemlerin çözümlerinin sonuçlarında önemli ölçüde sapmalar meydana gelmektedir. Holotransformasyon, uygun sonuçlar vermesi bakımından etkili bir yöntem olarak açıkça görülmektedir.
KAYNAKLAR
1. Holland, C.D., "Unsteady State Processes with Aplications in Multicomponent Distillation",
Prentice-Hall Inc. ,N. J., 1966
2. Robinson, C.S., Gilliland, E.R.,"Elements of Fractional Distillation", McGraw Hill, N. Y. , 1950
3. Lapidus, L., "Digital Computations for Chemical Engineers", McGraw Hill, N. Y. , 1962
4. Loomba, N.P.,"Lineer Programming", Tata-McGraw Hill, New Delhi, 1964
5. Aksoy, Yavuz,"İntegral Denklemler",Yıldız Üniversitesi Yayınları, İstanbul, 1983
6. Çağal, Behiç, "Sayısal Analiz", Seç Yayın Dağıtım, İstanbul, 1989
7. Benett, C.O., Myers, J.E.,"Momentum, Heat and Mass Transfer", McGraw Hill, Singapore, 1983
8. Kreyszig, E.,"Advanced Engineering Mathematics", John Wiley & Sons,N. Y. , 1972
9. Courant, R., Hilbert, D.,"Methods of Mathematical Physics", Interscience Publishers, N. Y., 1955
10. Perry, R.H., Editor-in-Chief,"Chemical Engineers' Handbook", McGraw Hill-Kogakusha Comp.,
Tokyo, 1963
11. Büyükkoca, E., "Statejik Üretim ve Savunma Endüstrisinde Holotransformasyon Uygulamasıyla
Spesifik ve Entegre Modellerin Kurulması-Çözüm Tekniklerinin Araştırılması",
Marmara Üniversitesi Araştırma Fonu Yayını, İstanbul, 1990
12. Büyükkoca, E., (Editor-in-Chief: Phyllis, S.G.) ,"Scientific and Technical Data in A New Era",
Hemisphere Publishing, Paris, 1990
13. Büyükkoca, E., "Optimizasyon ve Uygulamalı Matematik Modelleme", Ders notları, 1990