|
Checking Company Size
How "flat" can a company be? |
|

|
T here are a many ways to analyse a companyís performance to determine the most optimal size of a company.
Complicated (econometric) models can tell us how to be "lean an mean" by downsizing, reducing costs and raising profits.
Does a simple solution exists? |
One of the more intuitive methods is to judge the scale of a company by looking at the number of management-levels (MLís). Companies with a lot of MLís often have a tendency to be bureaucratic, ineffective and not market-fit. They are said to be top-down-managed and primarily relaying on the initiatives of their management instead of their employees. On the other hand companies with only a few MLís are said to be quite the opposite and are supposed to be flexible and profit-driven.
Whatever the companies mission, goal, HRM-philosophy, organisation structure (divisions, matrix, etc) or background are, managing a large company with a lot of employees certainly "demands" a minimum amount of MLís to "control", "co-ordinate" and "handle" the company and guarantee thereby its future.
Thatís why even large companies try to minimise their MLís to become as "flat" as possible. Flattening the companyís size is however a limited process.
Between the two variances of "all chiefs, no Indians" and "all Indians, no chiefs", the world of "common sense" exists. Nevertheless it maybe useful to develop a model, as a kind of check, to get sight on wetter the number of MLís in a company is relatively high, medium or low.
Simple model
In studying on how flat an organisation can be, we start by defining a very simple model that only depends on the next variables in the organisation:
|
N |
= |
Number of management-levels (or organisation-levels) |
|
S |
= |
Span of control (in this model constant) of each manager in the organisation |
|
M |
= |
Number of managers in the organisation |
|
T |
= |
Total number of employees in the organisation |
The relation between these variables can be given by the next formulae:
Formula I
| |
|
( S(N+1) - 1 ) |
T |
= |
|
| |
|
( S - 1 ) |
|
Formula II
R
Example
Suppose youíre the manager (the boss!) of an SME (see image below).
The "span of control" in your organisation is three. So you (as the boss) are managing three managers (supervisors) and each supervisor manages three other employees.
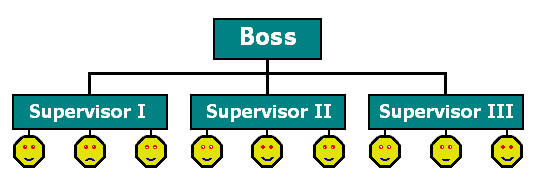
So in this case it follows:
S = 3
N = 2 (two levels of management)
T = 13 = 9 employees + 3 managers + 1 boss(manager)= (3(2+1)-1)/(3-1)
M = 4 managers (3+1) = (32
-1)/(3-1)
Flatness
Letís define the "flatness" of an organisation by the number of managementlevels [N]. Now we can derive the next formula for a minimal number of MLís [Nmin] an organisation needs to "manage" the total of given employees [T] of a company, given an assumed fixed span of control [S] for every manager:
Formula III
| |
|
|
Ln[ 1 + T x ( S - 1 ) ] |
Nmin |
= |
-1 + |
|
| |
|
|
Ln[ S ] |
|
From this simple model we can construct the next table that shows us how Nmin and T are related, for each S.
Table 1
Minimal amount of managementlevels
Nmin * in an organisation
as a function of the span of control [S] and the total of employees [T]
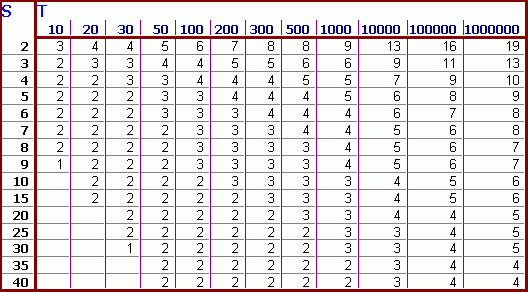
*) Nmin rounded upward to the next integer]
R
Example
Suppose your company consists of 100 employees (T=100; including yourself, staff, etc.) and you think that a span of control of 9 (S=9) is the absolute maximum in your company. From the table above (table 1) we conclude that you need a minimum of 3 managementlevels to run the company. However should you decide to reorganise your company with a span of control of 10 (S=10), two managementlevels would be sufficient.
Of course this kind of decisions is not only taken upon mathematical models, but strongly depends on all kind of other factors, as mentioned earlier.
Span of Control
From experience we know that the maximum span of control of a common manager varies between 3 and 15 people, and depends on several factors. The average span of control in companies is about 9 to 10 people. Middle managers with similar and streamlined activities in their department can perhaps manage a maximum span of control of 15 or 20 people. Top management on the other hand often can manage only a maximum of 3 to 6 sub-managers.
If you want to know more about this subject or want to calculate your personal span of control, please click on:
The span of control.
Practical Flatness Conclusions
From table 1 and the knowledge we have about the span of control we can draw some interesting practical conclusions about the optimal flatness of an organisation.
To do so we divide table 1 in different parts, as you see in table 2.
Table 2
Minimal and optimal amount of managementlevels
N in an organisation
as a function of the span of control [S] and the total of employees [T]
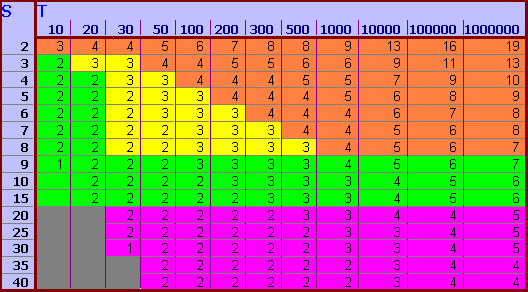
In table 2 we can distinguish several coloured areas:
Green area: Optimal +
This area consists of the average span of controls between 9 and 15 for companies varying between 30 and 1milion employees. As you can see in most cases you can run the company with 2 to 4 managementlevels. Only in extreme large companies with more than 100000 employees need one or two more additional managementlevels. If your company has more levels, you should strongly consider reorganising to fewer managementlevels.
The other part of the green area consists of SMEís (up to 30 employees) with (mostly) two managementlevels. In these cases the optimal span of control is often indeed smaller than 9 or ten, due to the activity, specialisation and / or geographical spread of the company.
Yellow area: Optimal
Just as in the green area your company is reasonably optimal sized. However in some cases you can try to increase your span of control. This will often not directly lead to fewer managementlevels, but will lower the amount of managers needed, lowers your level of costs and improve your profits.
Purple area: Efficient but Inflexible
This area consists of different type of companies. Itís obvious that these companies work extremely efficient. However, the span of control is extremely large. In a stable commodity where no new products have to be developed this can be fine. However if the market changes, the company can be in great treble. In this situation you have to have at least some departments (product-development; marketing) with a smaller span of control.
Orange area: Inefficient
In these companies there are four or more managementlevels. The costs of management, staf and communication in these types of companies will extremely rise and lead to inefficiency and loss of profits. Seriously reconsider a reorganisation to fewer managementlevels and another organisation-structure.
J.N. Berkemeijer, July 2002
Response : mailto:[email protected]



