Моделированиe орбитального движения

Интегрирование уравнений орбитального движения. 2

Введение

Моделирование орбитального движения (как невозмущенного, так и возмущенного) сводится к решению системы обыкновенных неоднородных дифференциальных уравнений второго порядка (уравнений движения):

(1)

где:

r – вектор координат тела

m – гравитационная постоянная центрального тела

f(r,t) – ускорение, создаваемое возмущающими силами

Даже для невозмущенного движения нахождение решения в явном виде сопряжено с определенными трудностями. В случае же наличия возмущений, точное решение, как правило, не существует (точнее, существует, но не выразимо в элементарных функциях). Мы рассмотрим методы нахождения приближенных решений.

Общие методы

Для приближенного решения движения могут быть использованы общие методы численного решения дифференциальных уравнений: Эйлера, Рунге-Кутты, Адамса и т.д.

Общие методы решения дифференциальных уравнений не делают предположений о виде правой части системы (1). С одной стороны, это делает их универсальными; с другой стороны, если функция в правой части известна, то, возможно, существует более точный метод решения.

Так, например, если отсутствуют возмущения, то движение тела описывается законами Кеплера. В этом случае уравнения движения могут быть проинтегрированы точно и нет никакой необходимости прибегать к приближенным численным методам. Решение уравнений невозмущенного движения приведено в следующем разделе.

Метод оскулирующих элементов

Если возмущающие силы малы (по сравнению с силой притяжения центрального тела), то движение тела в течение небольшого промежутка времени будет слабо отличаться от кеплеровского. Если мы рассмотрим изменение параметров орбиты во времени, то получим семейство орбит, которые будут касаться (оскулировать) с истинной траектория движения.

Суть метода оскулирующих элементов состоит в следующем: на каждом интервале тело предполагается движущимся по отрезку кеплеровской орбиты, по которой бы оно двигалось в отсутствие возмущений (т.н. оскулирующая орбита). Затем, с учетом возмущающих сил, параметры орбиты пересчитываются и вычисляется новая оскулирующая орбита. При этом действие возмущающих сил на интервале считается мгновенным.

Полученное таким образом приближение будет более точным, чем полученное с помощью общих методов (при сравнимой длине шага). Это объясняется тем, что мы точно учитываем влияние доминирующей силы – силы тяготения центрального тела.

Метод оскулирующих элементов подробно разобран в главе 4.2 книги А.В. Алёшин, О.В. Половников "Основы теории полета космического аппарата".

Интегрирование уравнений орбитального движения

Законы сохранения

Запишем законы сохранения в полярных координатах:

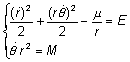(2)

где:

E, M – удельные энергия и момент имульса

m – гравитационная постоянная центрального тела

Перигей и апогей

Некоторые простые результаты можно получить даже без интегрирования уравнений движения.

Так, из системы (1) следует, что:

(3)

Легко видеть, что:

а) если Е < 0, то: r_min ≤ r ≤ r_max

b) если Е > 0, то: r ≥ r_m_ах

где:

Таким образом, мы нашли высоту перигея и апогея орбиты.

Отсюда находим скорость в апогее и перигее:

Разделение переменных

Преобразуем систему (1) к виду:

(4)

Обратите внимание на неопределенность знака при dr. Положительные значения соответствуют половине орбиты, на которой высота растет, отрицательные – половине, на которой высота уменьшается.

Обозначим также (считая Е≠0):

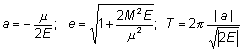
Траектория

Найдем траекторию движения, т.е. зависимость r(q).

Произведем замену:

, где r = a (1 - e²)

Тогда, из уравнения (4):

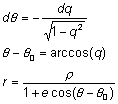
Мы получили первый закон Кеплера: траектория движения является коническим сечением. При этом легко видеть, что введенные ранее величины соответствуют параметрам конического сечения:

е – эксцентриситет

a – большая полуось

Значение q₀ соответствует перигею. Угловое расстояние от перигея u = q – q₀ называется истинной аномалией.

Зависимость от времени

Как мы увидим, в общем случае, зависимость координат от времени не выражается в элементарных функциях. Однако, обратная задача разрешима: мы можем явно выразить зависимость времени от координат.

Результат интегрирования зависит от знака E. Рассмотрим случаи: Е<0, Е>0, а также особый случай E=0. Эти случаи соответствуют эллиптической, гиперболической и параболической орбитам соответственно. Во всех случаях t₀ соответствует моменту прохождения через перигей.

a) E < 0 (эллипс)

Произведем замену:

Тогда:

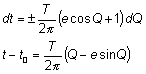
При этом:

· Т > 0 - период орбиты (получаем третий закон Кеплера)

· Q – эксцентрическая аномалия (получаем уравнение Кеплера)

b) E > 0 (гипербола)

Произведем замену:

Тогда:

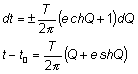
c) E = 0 (парабола)