Оптимальное управление
для орбитального носителя
Оглавление
Нахождение оптимального управления
Управление в плоском поле тяготения
Задача достижения заданой высоты
Управление в центральном поле тяготения
Управление с учетом лобового сопротивления
Управление с учетом аэродинамики
Ограниченное управление с учетом аэродинамики
Аэродинамика при трансзвуковых скоростях
Аэродинамика при гиперзвуковых скоростях
Сравнение различных программ управления
С учетом центральности гравитационного поля
С учетом ограничений на старте
Программа с учетом а-д сопротивления
Общая теория
Постановка задачи
Рассмотрим управляемую систему, движение которой описывается системой из n дифференциальныx уравнений:
![]()
где:
x – вектор состояния системы
u – вектор управления
Пусть также заданы некоторые граничные условия для x0, xT.
Пусть нашей задачей является нахождение оптимального управления u*, которое доставляет минимум функционалу:
![]()
Такая задача называется задачей Больца. Ее частными случаями является задача Лагранжа (f=0) и задача Майера (F=0). Частным случаем задачи Лагранжа является задача оптимального быстродействия (F=1).
Принцип максимума Понтрягина
Введем сопряженные переменные y1 ...yn , такие что:
![]()
где H(x, y, u, t) – функция Гамильтона:
![]()
Согласно принципу максимума Понтрягина, оптимальное управление u* должно доставлять максимум функции Гамильтона (необходимое условие оптимальности):
![]()
где G – ограничения, накладываемые на управление: u(t) Î G
При отсутствии ограничений управления, максимум часто можно найти из условия:
![]()
Кусочно-оптимальные решения
Вариационные методы, описанные выше предполагают непрерывность и дифференцируемость оптимального управления (класс C1). На самом деле, оптимальное управление далеко не всегда обладает этим свойством.
Так, например, рассмотрим следуюший пример: пусть ракете требуется попасть из точки А в точку B за минимальное время. При этом в начальной и конечной точке ракета должна иметь нулевую скорость, ускорение постоянно, а внешние силы отсутствуют. Оптимальное управление в таком случае будет следующим: половину пути максимально разгоняться в направлении точки B, а вторую половину максимально тормозить. Такое управление имеет разрыв в середине пути.
Таким образом, непрерывное решение, удовлетворяющее принципу максимума Понтрягина, не обязательно является оптимальным. Более того, оно может не являться оптимальным даже в классе непрерывных функций.
Предположим, что мы нашли непрерывное решение, удовлетворяющее принципу Понтрягина и граничным условиям. Предположим, что оптимальное управление является разрывным. Рассмотрим управление, достаточно близкое к оптимальному (разрывному), но все же непрерывное и дифференцируемое, и пусть оно также удовлетворяет граничным условиям. Такое управление будет более оптимальным, чем найденное с помощью принципа максимума.
Этот кажущийся парадокс объясняется следующим образом: принципу максимума удовлетворяют управления, которые оптимальны (являются экстремумом) в своей достаточно близкой окрестности. В нашем случае, управление, близкое к оптимальному (разрывному), экстремумом не является: всегда существует управление еще более близкое к оптимальному и экстремум не достигается в классе непрерывных функций.
В таких случаях, в практике, решение ищется в классе кусочно-дифференцируемых функций. Такое управление удовлетворяет принципу Понтрягина внутри каждого участка дифференцируемости, но может иметь разрывы.
Нахождение оптимального управления
Рассмотрим вначале нахождение решения в классе дифференцируемых функций. Нам известно начальное состояние системы. Предположим, что нам также известно начальное значение сопряженных переменных. Оптимальное управнение в любой момент однозначно определяется состоянием системы из принципа максимума Понтрягина. Тогда, решая совокупно основную и сопряженные системы дифференциальных уравнений (задача Коши), мы можем найти конечное состояние системы.
Таким образом, задача свелась к нахождению таких начальных значений для сопряженных переменных, которые обеспечивают требуемое конечное состояние системы. В общем случае эта задача решается численно и, при большом числе переменных, может быть достаточно трудоемкой.
Перейдем теперь к нахождению управления в классе кусочно-дифференцируемых функций. Предположим, нам известно число разрывов управления n, моменты разрывов ti и состояния системы ui в эти моменты. Тогда, решая предыдущую задачу для каждого интервала, мы можем получить управление, которое будет оптимально для данного набора {n, ti, ui}.
Задача свелась к оптимизации (в общем случае, численной) по набору параметров {n, ti, ui}. На каждом шагу оптимизации мы должны решать n+1 задач нахождения оптимального управления в классе дифференцируемых функций, способом, описаным выше. Излишне говорить, насколько трудоемкой может оказаться эта задача.
Движение ракеты
В этом разделе мы будем использовать следующие предположения:
- тяга и ускорение ракеты детерминистически заданы
- мы рассматриваем некоторую (мы будем использовать несколько) физическую модель
Мы будем решать следующую задачу: с учетом заданной программы тяги, какова оптимальная программа тангажа* (с рамках предположений физической модели)?
Здесь мы определяет оптимальную программу, как такую, которая выводит полезную нагрузку на заданную высоту с заданной (обычно нулевой) вертикальной скоростью и максимальной горизонтальной скоростью**.
(*) тангажом называют угол между главной осью аппарата и местным горизонтом.
(**) для интересующихся Теорией Оптимального Управления, заметим, что для подобной задачи, оптимальность может быть определена и по-другому – однако, результат при этом будет тем же.
Управление в плоском поле тяготения
Рассмотрим применение принципа максимума на простом примере.
Пусть ракета движется в плоском однородном поле тяготения.
Уравнения движения:
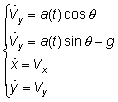
где:
a(t) – характеристическое ускорение
q – угол тангажа
Функция Гамильтона:
![]()
Здесь и далее: через yx, yy обозначены сопряженные переменные, соответствующие Vx, Vy, а через jx, jy – соответствующие x, y.
Применяя принцип максимума, получаем:
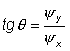 (1)
(1)
Сопряженная система:
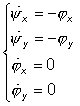
Легко видеть, что в данном случае, оптимальная программа для тангенса угла тангажа является дробно-линейной:
![]() .
.
Свободные коэффициенты однозначно (с точностью до множителя) определяются граничными условиями.
Задача достижения заданой высоты
Упростим предыдущую задачу и вместо попадания в заданную точку, будем требовать только достижения определенной высоты. Тогда:
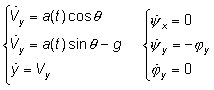 (2)
(2)
В данном случае, оптимальная программа упрощается и становится линейной:
![]()
Управление в центральном поле тяготения
Перейдем во вращающуюся систему координат, связанную с центром Земли и ракетой. Вводя в уравнения центробежное и кориолисово ускорения:
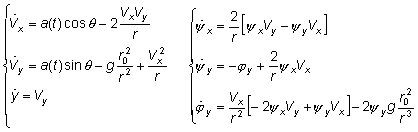 (3)
(3)
Здесь:
r – расстояние до центра Земли (r ≡ y + r0); r0 – радиус Земли.
Решая совместно основную и сопряженную системы, определяем оптимальное управление из соотношения (1):
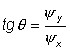
Управление с учетом лобового сопротивления
Рассмотрим оптимальное управление для упрощенной аэродинамической модели, в которой учитывается лобовое сопротивление (вектор аэродинамической силы параллелен вектору скорости). Эта модель не учитывает подъемной силы и, следовательно, применима только в случае, когда либо угол атаки либо аэродинамическое качество крайне малы.
Запишем силу а-д сопротивления в виде:
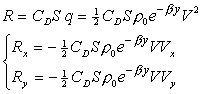
где:
q = ½rV2 – скоростной напор
Cx – а-д коэффициент сопротивления
S – характерная площадь
r0 – плотность воздуха на уровне моря (y=0)
b – коэффициент падения плотности с высотой
Основная и сопряженная системы:
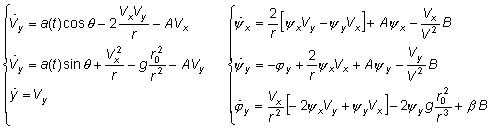
где:
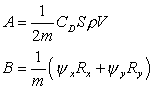
Как и в предыдущем примере, решая совместно основную и сопряженную системы, определяем оптимальное управление из соотношения:
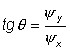
Аэродинамическая модель
В более общем случае (для ненулевых углов атаки), общую аэродинамическую силу уже нельзя считать параллельной вектору скорости. Задача точного определения а-д силы крайне сложна и для тел сложной формы обычно решается эксперементально (продувкой в а-д трубах). Решение представляется в виде экспериментальных таблиц или аппроксимирующих кривых.
Следующая модель обычно используется в качестве приближения. Она неплохо оценивает а-д силу при небольших (до ~15 градусов) углах атаки.
В скоростной (связанной с вектором скорости) системе координат:
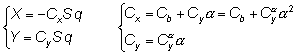
где:
a – угол атаки (угол между а-д осью аппарата и вектором скорости)
q – скоростной напор
Cx – коэффициент лобового сопротивения
Cy – коэффициент подъемной силы
(*) Заметим, что здесь мы пренебрегаем вязким трением.
Мы будем использовать тригонометрическое представление этой модели в связанной (с осями тела) системе координат:
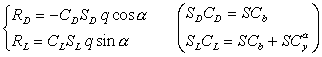 (4)
(4)
где:
RD, RD - проекции а-д силы на оси тела (главную и нормальную)
SL, SL - характерные площади тела (мидель и нормалльная проекция)
(**) Обычно значения а-д коэффициентов приводятся к одной площади (крыла), но здесь мы будем использовать две разные площади: площадь миделева сечения (характерная площадь лобового сопротивления) и площадь нормальной проекции (характерная площадь подъемной силы).
Нетрудно убедиться, что оба представления идентичны с точностью до o(a2)
При наличии у аппарата аэродинамического качества возникает возможность управлять подъемной силой, меняя угол атаки. При этом направление вектора тяги не обязательно должно совпадать с аэродинамической осью аппарата. Таким образом, возникает еще один независимый параметр управления:
c - угол между а-д осью аппарата и горизонтом
Через q мы, как и прежде, будем обозначать угол между вектором тяги и горизонтом.
Управление с учетом аэродинамики
Для выбранной аэродинамической модели, уравнения движения имеют вид:
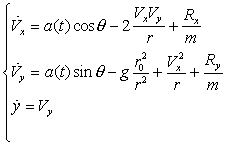 (5)
(5)
где:
Rx = RD cosc – RL sinc = -q [ CDSD cosa cosc + CLSL sina sinc ]
Ry = RD sinc + RL cosc = -q [ CDSD cosa sinc – CLSL sina cosc ]
- проекции а-д силы на оси основной (орбитальной) системы координат
Выражая угол атаки a через угол тангажа и компоненты вектора скорости, после подстановок и преобразований, получаем сопряженную систему:
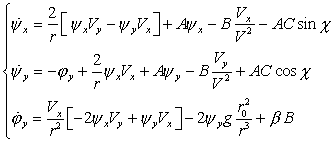 (6)
(6)
где:
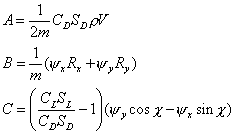
Заметим кстати, что выражение:
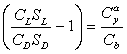
имеет непосредственое отношение к аэродинамическому качеству, которое определяется как:
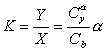
В отсутствие ограничений на q и c, максимум гамильтониана соответствует:
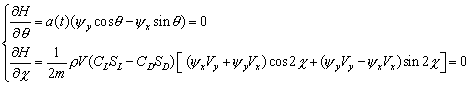 (7)
(7)
Таким образом, оптимальное управление {q, c } удовлетворяет:
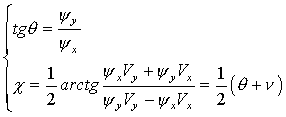
где:
n – угол между вектором скорости и горизонтом
Мы получили любопытный результат:
Oптимальным направлением для а-д оси аппарата является биссектрисса угла, образованного векторами скорости и тяги. (8)
Для модели (4) это соотношение справедливо в точности. Кроме того, для довольно широкого класса аэродинамических моделей оно справедливо с точностью до о(a2).
Ограниченное управление с учетом аэродинамики
В предыдущем разделе мы предполагали, что ориентация аппарата c произвольна и не зависит от направления тяги q. Во многих случаях это не так. Например, для обычной ракеты, вектор тяги и ось аппарата должны совпадать (q = c). Мы рассмотрим несколько общий случай: q = c + g 0.
Найдем оптимальное управление для этого особого случая:
![]()
или, после преобразований:
![]() (9)
(9)
где:
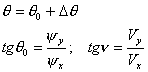
Тригонометрическое уравнение (9) сводится к алгебраическому уравнению четвертой степени. Решив его, мы получим оптимальное управление q*. Хотя уравнение четвертой степени может быть решено в радикалах (например, методом Ферро), формула для его решения достаточно громоздка. Ниже изложен простой метод для его приближенного решения.
Исходя из общих представлений, мы можем предположить, что оптимальное значение q* не должно слишком сильно отличаться от q0 – т.е. Dq мало. Разложив в ряд по Dq до O(Dq), получим:
![]()
где:
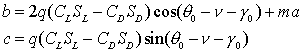
Аналогично, используя разложение до O(Dq2) и решая квадратное уравнение, можно получить более точное приближение для Dq:
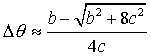
Аэродинамика при трансзвуковых скоростях
До сих пор мы предполагали, что а-д коэффициенты являются константами. На самом деле, при скоростях сравнимых со скоростью звука, коэффициенты довольно сильно зависят от скорости. Так, например, коэффициент сопротивления резко возрастает в трансзвуковом диапазоне, а затем снижается:
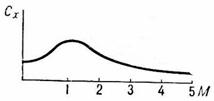
В целом, зависимость а-д коэффициентов от скорости является довольно сложной, сильно зависит от формы тела и определяется экспериментально (продувкой в а-д трубах)
... in progress…
Аэродинамика при гиперзвуковых скоростях
На гиперзвуковых скоростях меняется характер зависимости а-д сил от угла атаки. Например, подъемная сила становится пропорциональной a2 (ньютоновское обтекание).
... in progress…
Оптимальная программа тяги
До сих пор мы предполагали, что тяга ракеты предопределена. Это не всегда так. Для многоступенчатой ракеты, в случае одновременной работы нескольких ступеней возникает вопрос выбора оптимальной программы тяги (дросселирования).
Для достижения максимальной характеристической скорости, оптимальной является строго последовательная схема работы ступеней. Однако, при этом уменьшается тяга и увеличивается длительность активного участка. Следовательно, растут гравитационные потери. Более того, для некоторых ракет, тяги первой ступени будет просто недостаточно для отрыва от старта. Требуется одновременная работа первой и второй ступеней.
Рассмотрим оптимальную программу тяги второй ступени (при одновременной работе первой). Для этого нам понадобится ввести дополнительную переменную состояния: массу.
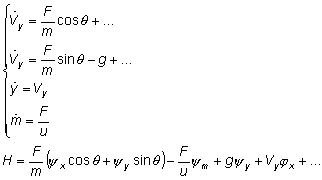
где u – скорость истечения продуктов сгорания
Обратим внимание, что сила тяги входит в гамильтониан линейно. Это означает, что максимум гамильтониана достигается либо при максимальном либо при минимальном значении тяги (в зависимости от знака выражения при F). Таким образом, оптимальная программа тяги должна состоять из интервалов минимальной и максимальной тяги.
Анализируя знак выражения при F, достаточно легко видеть, что в отсутствие а/д сопротивления, тяга второй ступени должна быть вначале максимальной, а затем (с какого-то момента и вплоть до отделения первой ступени) – минимальной (график слева).
В случае наличия а/д сопротивления возможно (но не обязательно) появление еще одного интервала минимальной тяги (график справа).
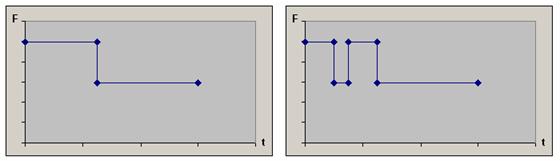
Заметим, что:
- Мы предполагаем, что скорость истечения продуктов сгорания (или удельный импульс) не зависит от величины тяги, т.е. от глубины дросселирования двигателя. Это не вполне так. Обычно глубокое дросселирование приводит к уменьшению удельного импульса. Тем не менее, вывод о том, что оптимальная сила тяги либо максимальна, либо минимальна, останется верным в случае, если зависимость удельного импульса от дросселирования не слишком велика.
- Приведенные графики демонстрируют общий вид оптимальной программы. В зависимости от конкретных массо-тяговых характеристик возможны любые частные случаи. Например: тяга второй ступени может быть максимальной (или минимальной) на всем притяжении работы первой ступени; «аэродинамический» интервал минимальной тяги может отсутствовать; и т.д.
- Ограничение на минимальную тягу, в принципе, может отсутствовать (Fmin=0). Однако, в реальности, как правило, глубокое дросселирование (или полное выключение) двигателей второй ступени или невозможно совсем или приводит к существенным потерям.
- Естественно, реальные программы тяги являются более сложными (что, вообще говоря, является отклонением от математической оптимальности). Такое усложнение программы тяги обьясняется различными ограничениями инженерного характера (подробнее см. в разделе «Ограничения по управлению»).
Ограничения по управлению
... in progress…
Сравнение различных программ управления
Сводная таблица
В следующей таблице собраны элементы системы уравнений движения и сопряженной системы для различных моделей управления. Эти элементы были более подробно разобраны выше в соответствующих разделах.

где:
r ≡ y+r0 – расстояние до центра Земли
r0 – радиус Земли
r = r0e-by – плотность воздуха
RD – сила лобового сопротивления
RL – подъемная сила
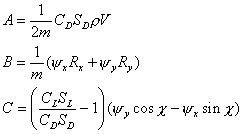
Линейная программа
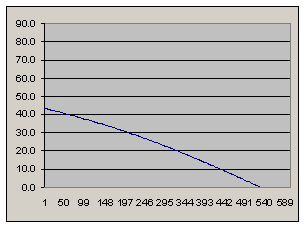
перигей: 200 км
апогей: 481 км
скорость в перигее: 7581 м/с
С учетом центральности гравитационного поля
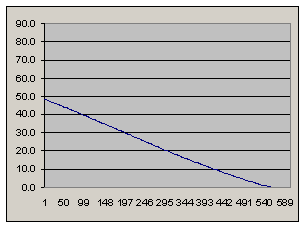
перигей: 200 км
апогей: 631 км
скорость в перигее: 7622 м/с
С учетом ограничений на старте
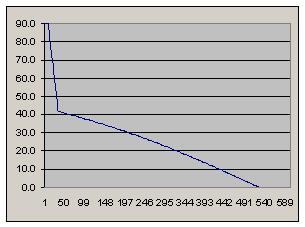
перигей: 200 км
апогей: 753 км
скорость в перигее: 7655 м/с
Программа с учетом а-д сопротивления
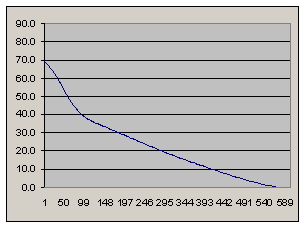
перигей: 200 км
апогей: 916 км
скорость в перигее: 7698 м/с
Реальные программы управления
... in progress…