F R A C T A L E S
F R A C T A L E S
El Conjunto de Mandelbrot
El Conjunto de Mandelbrot















El Conjunto de Mandelbrot (en honor a su descubridor, Benoit B. Mandelbrot del Centro de Investigaciones Thomas Watson de la IBM), no es otra cosa sino un conjunto infinito de puntos en el plano complejo que satisfacen determinadas condiciones.

En realidad, para no entrar en aburridas explicaciones matemáticas, vamos a explicar la construcción del conjunto con la ayuda de una analogía: el Autobús de Mandelbrot:
veamos pues el pizarrón para entender el procedimiento:





Los puntos que pertenecen al Conjunto son aquéllos que hacen que el recorrido del autobús describa una ruta que lo mantenga siempre a menos de 2 unidades del origen, independientemente del número de "paradas" que éste realice.

Para saber si un punto P(a,b) del plano pertenece al Conjunto de Mandelbrot debemos seguir el siguiente procedimiento:

  1. El autobús sale siempre del origen de coordenadas  Z0 = (0,0)

  2. De allí se dirige a la primer parada (en la que "tomaremos" el autobús). O sea: la primer parada debe ser siempre el punto de embarque, que siempre será el punto P(a,b) que queremos testar.

    Z1 = (a,b)

  3. La próxima parada será el punto Z2 = (x2,y2) , cuyas coordenadas están definidas por el siguiente algoritmo:

    Z2 = (Z1)2 + (a, b)

  4. De esto se deduce que para la "enésima parada n" :

    Zn = ( Zn - 1 )2 + (a,b)

    es decir        xn = ( x n - 1 ) 2 - ( y n - 1 ) 2 + a      

             yn = 2 xn - 1 yn - 1 + b         


  5. Si después de efectuar "infinitas" paradas, el punto Zn se encuentra a una distancia menor que 2 unidades del origen, entonces el punto P(a,b) en el cual "embarcamos" pertenece al Conjunto de Mandelbrot.


  6. En la práctica puede resultar complicado realizar un numero muy grande de iteraciones "paradas", de forma que se admite "delimitar" el conjunto de Mandelbrot por aproximaciones. Así, se construye una tabla de coloreado del siguiente tipo:

    si después de N=100 iter. Zn está a menos de 2 unidades ---> rojo
    si .............. de N=150 ......................................................... ---> azul
    si .............. de N=200 .................................................. ---> amarillo

    Aunque estos puntos no pertenezcan al conjunto, este truco permite obtener bellos efectos y explorar los alrededores fronterizos del conjunto.


En esta imagen podemos observar el recorrido el autobús para el caso en que el punto de análisis sea P(0.2,0.4). Es fácil calcular los sucesivos destinos (vamos a tomar como ejemplo 11 iteraciones):


   P0( 0, 0)
   P1( 0.2000, 0.4000)
   P2( 0.0800, 0.5600)
   P3(- 0.1072, 0.4896)
   P4(- 0.0282, 0.2950)
   P5( 0.1138, 0.3834)
   P6( 0.0660, 0.4872)
   P7(- 0.0330, 0.4643)
   P8(- 0.0145, 0.3693)
   P9( 0.0638, 0.3893)
   P10( 0.0525, 0.4497)

   P11( 0.0005, 0.4472)

Es evidente en este caso que después de 11 iteraciones (o paradas), nuestro autobús no se aleja del centro. Aunque aumentásemos el número de iteraciones para 1000 o 10k, el resultado sería el mismo: es decir, este punto pertenece al conjunto.

Pero, ¿que habría ocurrido si nuestro autobús se hubiese escapado al infinito después de, digamos, 150 iteraciones? En este caso deberíamos adjudicar un color para todos los puntos que (si bien no perteneciendo al conjunto), "se mantienen dentro de él hasta 150 iteraciones"...

Ciertamente habrá puntos en los que nuestro autobús sólo huye al infinito después de 106 iteraciones (o más), de forma que debemos determinar el numero de iteraciones que asociaremos a cada color para indicar "pseudo puntos del conjunto", los puntos que sí pertenecen al Conjunto de Mandelbrot los indicaremos con negro (por ejemplo...).







EL CONJUNTO Y EL PROGRAMA


Veamos el Conjunto de Mandelbrot tal como mostrado por mi programa:



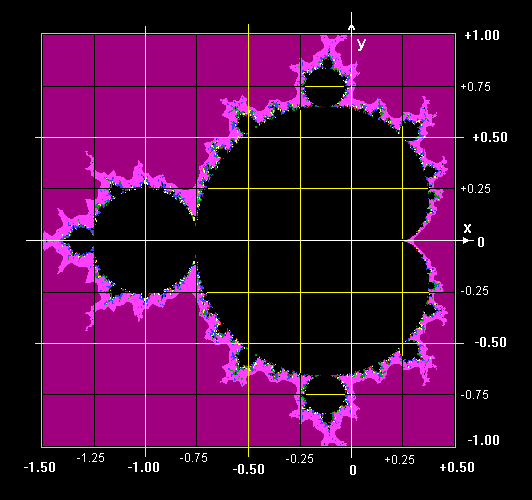
Esta es la imagen básica del conjunto, y vemos que inclusive con un número máximo de iteraciones relativamente bajo (Nmax=200), conseguimos tener una idea bastante clara de su extensión.

La necesidad de elevados números de iteraciones se torna clara cuando examinamos el conjunto en "ventanas de observación" relativamente pequeñas.

Es importante observar los sentidos positivos (+) de los ejes de coordenadas x e y para poder determinar las coordenadas de la "ventana de observación" al usar mi programa.

Para realizar el download del programa y conocer los principales aspectos de su uso, por favor proceda para la página correspondiente MBROT.EXE




Para ver una serie de aproximaciones sucesivas del conjunto, realizadas con mi programa, sírvase clicar en Tour por el Mandelbrot.


[email protected]
1