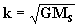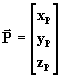
Cálculo de las Órbitas Planetarias
por Ing. Andrés Esteban de la PlazaÍNDICE:
CONSIDERACIONES SOBRE :
CÁLCULO DE ÓRBITAS NO ELÍPTICAS:
1. REPRESENTACIÓN DE VECTORES
LA posición de un punto P en el espacio puede ser definida por un vector posición
 con origen en un centro O de coordenadas ortogonales rectangulares.
Definiendo en esta terna xyz,
los versores (vectores unitarios) de los ejes, obtenemos
respectivamente : el versor
con origen en un centro O de coordenadas ortogonales rectangulares.
Definiendo en esta terna xyz,
los versores (vectores unitarios) de los ejes, obtenemos
respectivamente : el versor 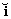 como versor de la
dirección x, el versor
como versor de la
dirección x, el versor 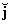 como el versor de la dirección y, y el versor
como el versor de la dirección y, y el versor
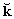 como el versor de la dirección z.
Así, cualquier vector definido en uno de estos ejes estará; representado por el producto
de un escalar igual al módulo y de un versor de la dirección
como el versor de la dirección z.
Así, cualquier vector definido en uno de estos ejes estará; representado por el producto
de un escalar igual al módulo y de un versor de la dirección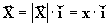 .
.

Por lo tanto, podemos descomponer el vector
 en sus componentes ortogonales
en sus componentes ortogonales
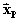 ,
, 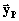 e
e
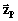 en un sistema de centro O:
( projecciones de
en un sistema de centro O:
( projecciones de  en los ejes x, y, e z ) de forma que
en los ejes x, y, e z ) de forma que  .
.
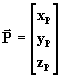

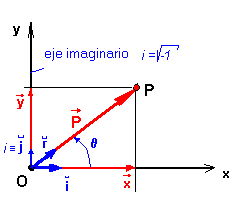
Pero esta no es la única representación posible para el punto P. Podemos imaginar un plano que contenga el vector
 y el centro O, de manera que, aunque aún continuemos en el
espacio tridimensional, la representación de
y el centro O, de manera que, aunque aún continuemos en el
espacio tridimensional, la representación de
 é es hecha en un plano,
y este plano será un plano complejo o sea, el eje x
será real, y el eje y será imaginario, o sea:
é es hecha en un plano,
y este plano será un plano complejo o sea, el eje x
será real, y el eje y será imaginario, o sea:
La ventaja de proceder así está dada por la posibilidad
de representar un número complejo en su forma exponencial, como un vector. Se observa
fácilmente que si definimos el versor 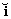 para la dirección x, la dirección de r
estará definida por un versor
para la dirección x, la dirección de r
estará definida por un versor 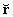 tal que
tal que
![]() donde
donde 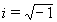 , entonces:
, entonces:
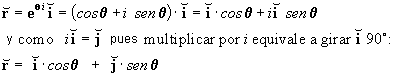
de forma que:
que es la expresión del radio vector en coordenadas polares.
2. ACELERACIÓN EN COORDENADAS POLARES
Podemos ahora proceder a derivar
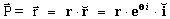 respecto del tiempo para
encontrar la aceleración. Antes vamos a calcular la derivada
con respecto al tiempo de
respecto del tiempo para
encontrar la aceleración. Antes vamos a calcular la derivada
con respecto al tiempo de 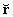 , pues es
una función de q, o sea que
, pues es
una función de q, o sea que
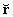 =
=
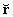 (q):
(q):
vamos a calcular entonces la primera derivada de
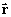 , o sea
, o sea
 :
:
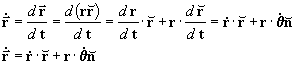
vamos a calcular ahora la segunda derivada de
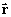 , o sea
, o sea
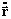 :
:
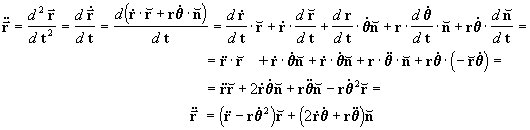
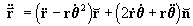
donde:

3. FUERZAS CENTRALES Y GRAVITACIÓN
Inicialmente vamos a deducir las fórmulas que determinan las trayectorias de los cuerpos que se encuentran sujetos a la atracciáon de fuerzas centrales, en el caso particular de la ley de gravitación universal, o sea

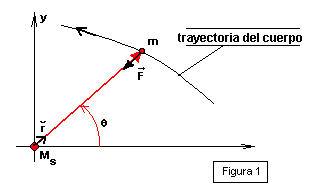
Donde el punto m está sometido a la fuerza :
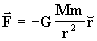
 es el versor (vector unitario)
de la dirección de
es el versor (vector unitario)
de la dirección de
 y:
y:
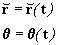
t = tiempo
MS = masa del cuerpo central
m = masa del objeto
La resolución de este problema debe proporcionar las siguientes funciones:
Las expresiones para la aceleración en función de las componentes normal y radial de la aceleración son:

Pero en los sistemas de fuerzas centrales sabemos que la aceleración normal es nula Þ an=0, de forma que la aceleración será:
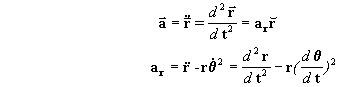
y recordando que la ecuación diferencial general del movimiento central en este caso es:
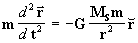
4. RESOLUCIÓN DE LA ECUACIÓN DIFERENCIAL DEL PROBLEMA
La ecuación diferencial general del problema puede ser descompuesta en dos particulares:

tenemos entonces:
mar = 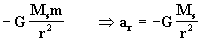
man= 
de esta forma la ecuación diferencial que tenemos que resolver será:

[1]
pero no conocemos las relaciones
 , pero acordándonos de la ecuación
[2] obtenemos que:
, pero acordándonos de la ecuación
[2] obtenemos que:
an = 0
Þ
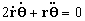
o sea

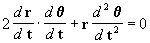 pero
pero

De
 podemos obtener
podemos obtener
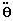 , o sea:
, o sea:
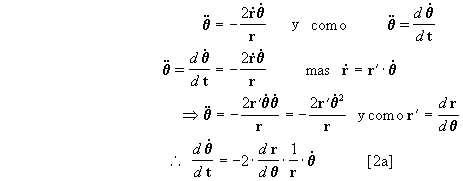
haciendo pasaje de términos en la [2 a] obtenemos:
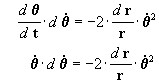
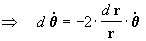

integrando ahora la [3]:

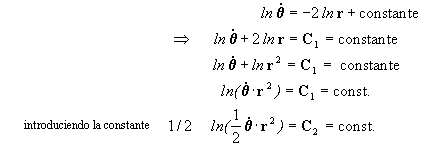
por lo tanto Þ
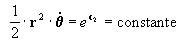
que no es otra cosa sino la velocidad areolar del punto m en su trayectoria como podemos observar en la figura 2:
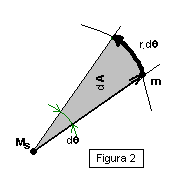
"los planetas barren áreas iguales en tiempos iguales" .
El área del triângulo será:
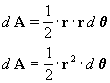
Vamos a hacer ahora algunas consideraciones energéticas. Para esto definimos:
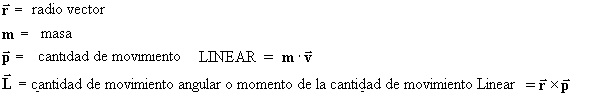

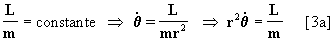
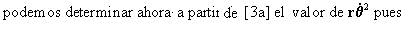
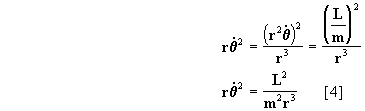
Así, para resolver la ecuación diferencial [1] , ya tenemos o valor
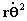 pero nos falta conocer el valor de
pero nos falta conocer el valor de
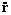 . Para esto, y volviendo ahora
a la aceleración radial:
. Para esto, y volviendo ahora
a la aceleración radial:
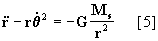
observamos que

Ahora, reemplazamos [6] y [4] en la ec. diferencial [5] y obtemos así:


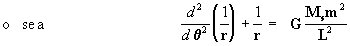
Haciendo 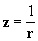 y
reemplazando, llegamos a una ecuación diferencial [7] de
fácil resolución:
y
reemplazando, llegamos a una ecuación diferencial [7] de
fácil resolución:


[7]
La solución general de la ecuación [7] está compuesta por
dos soluciones; la solución homogênea
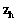 que proviene de resolver
que proviene de resolver
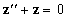 , y la solución particular
, y la solución particular
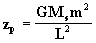 .
.
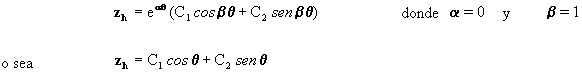
introduciendo ahora las constantes
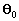 e
e
 de forma que:
de forma que:
llegamos a



de forma que

operando llegamos a
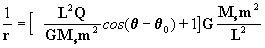
o sea

[8]
que obviamente corresponde a la ecuación de una cônica (Figura 3), cuya fórmula general es:

 [8aa]
[8aa]
o sea que:
 [8 a]
[8 a]
5. CONSIDERACIONES PARA LAS ÓRBITAS ELÍPTICAS
Los parámetros de la elipse en la Figura 4 sono:
a: semi-eje mayor
b: semi-eje menor
c=a2-b2
e: excentricidad = c/a
f: distancia focal =
![]()
A: área de la elipse =
pab=
![]()
T: período para uma revolución
|
La ecuación de la elipse en coordenadas cartesianas es: |
La ecuación de la elipse en coordenadas polares es: |
|
|
La velocidad con la que el radio vector r barre el área de la órbita vale:
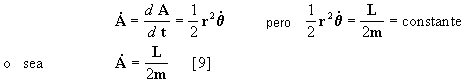
si ahora integramos la [9] en el tiempo T obtendremos la superficie total A:
![]()
![]()
ahora vamos a despejar T:
![]()
ahora vamos a calcular T2 recordando que
![]() , o sea:
, o sea:
![]() [10]
[10]
pero para el sistema solar, Ms=masa solar,
a=distancia media del planeta al sol, T=su período de
revolución. Analizando la ec. [10] es óbvio que la cantidad
![]() es una constante para todos los
planetas del sistema solar. Así tenemos
es una constante para todos los
planetas del sistema solar. Así tenemos ![]() en donde los subíndices 1,2, representan los diferentes planetas.
Tal es la 3a. Ley de Kepler: "los cuadrados de los períodos
de revolución de los planetas son inversamente proporcionais a sus
distancias medias al sol".
en donde los subíndices 1,2, representan los diferentes planetas.
Tal es la 3a. Ley de Kepler: "los cuadrados de los períodos
de revolución de los planetas son inversamente proporcionais a sus
distancias medias al sol".
6. CÁLCULO DE LA POSICIÓN EN LA ÓRBITA ELÍPTICA
Hasta ahora descubrimos la función r=r(q), de forma que sabemos cuál será el tipo de curva descripta por el punto m sin embargo, falta conocer cuál es la función que determina las variaciones de q en función del tiempo t, o sea, la función q =q(t).
Sabemos que para la elipse, en coordenadas polares, la posición del punto de masa m está definida por la relación r( q ), pero no conocemos la dependencia de los parámetros r y q en función del tiempo t. Vamos a deducirlas:
la velocidad areolar es:
por lo tanto, después de haber descripto um ângulo q en la trayectoria, en un tiempo t, el punto m habrá barridp varrido un área A q que será la resultante de haber integrado:

pero para tener los límites de integración en función de q :
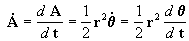
![]()
y eliminando
 :
:
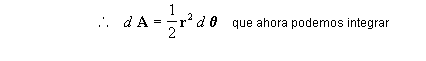
portanto  [11]
[11]
Sustituyendo
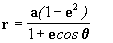 en la integral de arriba y
multiplicando por 2, tenemos:
en la integral de arriba y
multiplicando por 2, tenemos:
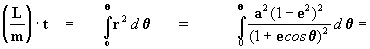
entonces
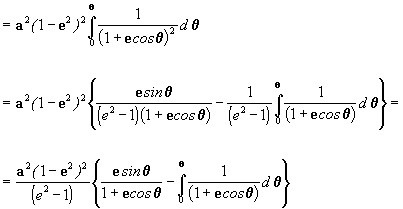
pero para la elipse Þ e < 1 Þ e2 < 1 así la solución de la
 será:
será:
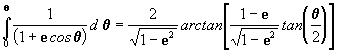
entonces
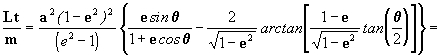
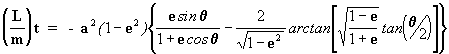 [12]
[12]
Esta fórmula es muy linda pero el resultado obtenido es el inverso de aquél que deseábamos, en realidad nosotros queríamos q =q (t) y terminamos obteniendo t=f(q ). Es fácil observar que despejar q nos leva a uma ecuación muy compleja, o se, debemos encontrar otro método.
Introducimos ahora una cantidad auxiliar E denominada anomalía excéntrica, que cumple
la siguiente condición:
 [12a]
[12a]
que equivale a decir que

entonces introduciendo la [12a] en la [12], tenemos:
 [13]
[13]
se puede demostrar que para la cantidad auxiliar E introducida:
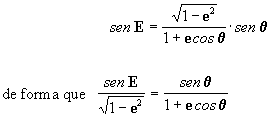
sustituyendo esta última en la [13] llegamos a:

así
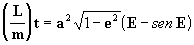 [14]
[14]
 [15]
[15]
para la Tierra Þ
T=Tt e at= 1 ua (unidad
astronómica),
Þ
entonces para cualquier planeta con T, a, tenemos (aplicando [10]) que:
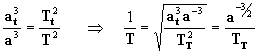 [16]
[16]
e sustituyendo la [16] en la [15] obtenemos: 
o sea que la [14] queda:

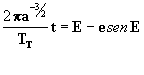 [17]
[17]
Esta última fórmula es básica, pues es la empleada en el cálculo de las efemérides.
Las siguientes denominaciones son las usuales:
q
= anomalía verdadera [radianos] =
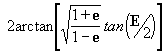 [18]
[18]
E = anomalía excéntrica =
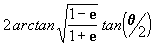 [radiánes]
[radiánes]
a = distancia media al sol [ua] (unidades astronômicas)
n = movimiento diurno medio =

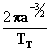 [radianes/día]
[radianes/día]
n = k
 donde k=constante de Gauss =
donde k=constante de Gauss =
 [18a]
[18a]
M = anomalía media = n Dt [19]

así las fórmulas se reducen a:
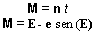
sendo t = tiempo desde el último paso por el perihelio, em dias.
TT = año trópico = 365.256374 días
El proceso de cálculo se reduce a determinar la anomalía media M [19], y con esto procedemos a calcular la anomalía excéntrica E que satisface la ecuación de Kepler [20], así calculamos q según la [18]. Con q calculamos r , lo que determina la posición del punto m en la órbita. La resolución de la Ecuación de Kepler se realiza por iteraciones sucesivas, de forma que el algoritmo de cálculo es el siguiente:
D
t=T-T0 donde T0 es la fecha del último paso por el
perihelio
a = distancia me al sol
Nota: Normalmente el tiempo del paso T0 está dado en días Julianos JD, de forma que la fecha de cálculo también está en días julianos y el cálculo de D t se reduce apenas a encontrar la diferencia (en días julianos) entre T y T0.
El diagrama de flujo del algoritmo es:
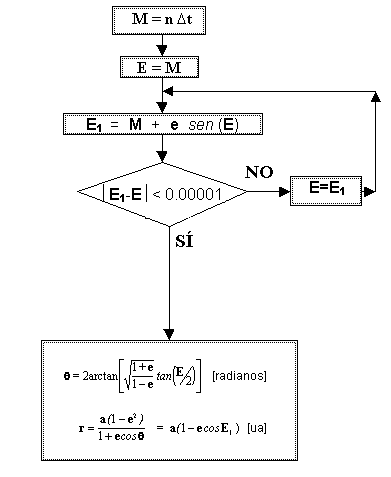
Vamos a resolver un ejemplo de aplicación: caso Júpiter
a = 5.208174 ua ; e = 0.049284
T = 2450896.510556 dj =24 Marzo 1998
T0 = 2446966.84378 dj =24 Junio 1987 (perihelio)
D t = 3929.666776 dj
n = 0.00144728573606
M = n D t = 5.687350672374 radianes ( =325°.861190138)
E=M= 5.687350672374
E1=M+e senE= 5.659692503366
E1-E= -0.0276581690088
E=E1= 5.659692503366
E1=M+e senE=5.658575010
E1-E=-0.001117493
E=E1=5.658575010
E1=M+e senE=5.658530316
E1-E=-0.000044694
E=E1=5.688530316
E1=M+e senE=5.658528529
E1-E=-0.000001787
E=E1=5.658528529
y como senE =
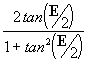 =-0.584818898 Þ
<0 Þ estamos en el IV cuadrante!
=-0.584818898 Þ
<0 Þ estamos en el IV cuadrante!
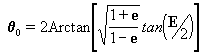 = -0.654082984
= -0.654082984
q = 2p + q 0 = 2p + (-0.654082984) = 5.629102324 radianes = 322° .5238
así
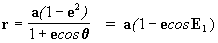 = 4.999964739 ua
= 4.999964739 ua
Según la efemérides, para la fecha 24/03/1998, la anomalía media vale 325° 33¢35 ² , la distancia al sol es 5.00079 ua. Comparando con nuestros valores, nuestra anomalía media fue 325° 51¢40² , y la distancia 4.999964739 ua (una diferencia de 0.016%). Vale la pena recordar que en la fecha de paso por el perihelio existía una imprecisión con respecto a la hora, se la hubiésemos sabido, la diferencia sería aun menor! También, se consideramos que Júpiter da una vuelta en 11.86 anos, desde el perihelio hasta la dfecha de cálculo pasaron 10.758 años, o sea un poco menos de 1 revolución lo que concuerda con nuestros cálculos.
Después de conocer la posición en la órbita, y sabiendo los parámetros orbitales (i: inclinación de la órbita con respecto a la eclíptica, W : longitud del nodo ascendiente y w : argumento del perihelio podemos pasar de las coordenadas polares para las rectangulares (coordenadas heliocéntricas orbitales), para las heliocéntricas eclípticas, y conociendo la posición de la Tierra (en coordenadas heliocéntricas eclípticas, la diferencia nos da; el vector Tierra-Júpiter, o sea las coordenadas geocéntricas eclípticas de Júpiter, entonces sólo falta una última transformación, para las coordenadas geocéntricas ecuatoriales ( r: distancia Tierra-Júpiter , a: ascensión recta, d: declinación). Tales cálculos se efectúan empleándose matrices y análisis vectorial (fórmulas de Euler).
Para facilitar el cómputo de la anomalía verdadera y la determinación del cuadrante en cuestión tal vez resulte más útil el empleo de las siguientes fórmulas, recordando que la fórmula:
 retorna el argumento q
en su valor principal, o sea q
0, en los I y IV cuadrantes.
retorna el argumento q
en su valor principal, o sea q
0, en los I y IV cuadrantes.

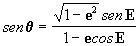
Assim:
cosq = 0 sen q > 0 q = q0Þ q 0 = 90°
cosq = 0 sen q < 0 q = q 0Þq 0 = 270°
cosq > 0 sen q > 0 q = q 0Þq 0 > 0° 0 ° < q < 90°
cosq < 0 sen q > 0 q = 180° + q0 Þ q 0 < 0° 90° < q < 180°
cosq < 0 sen q < 0 q = 180° + q0Þ q 0 > 0° 180 ° < q < 270°
cos q > 0 sen q < 0 q = 360° + q 0 Þq 0 < 0° 270 ° < q < 360°
También durante el cálculo debemos observar que:
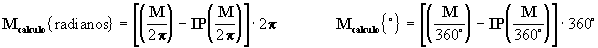
Mcálculo{rad} = [ (9.28/2p ) - IP(9.28/2p)]2p = [1.4769579 - 1]2p =
= [0.4769579]2 p = 2.9968147 rad
Mcálculo { °} = [ (531° .7048339/360°) - IP(531.7048339/360 °)]360° = [ 1.4769579 - 1]360° =
= [0.4769579] 360 ° = 171° .7048339
7. CONSIDERACIONES SOBRE LA CONSTANTE DE GAUSS, EL MOVIMIENTO DIURNO MEDIO Y LA FÓRMULA DE KEPLER
Dada la ecuación [14] :
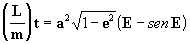 , y como:
, y como:
M = E - sen(E) =
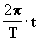
Aelipse = p
ab = p
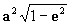
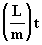 = 2At
(siendo At el área barrida hasta el
instante t )
= 2At
(siendo At el área barrida hasta el
instante t )
resulta que la ecuación [14] equivale a:
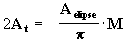 [20a]
[20a]
que encontramos fue a expresión del doble del área orbital barrida en un tiempo t desde el perihelio. Por otro lado, si en la ec. [20a] despejamos M obtenemos la ec. [20aa], así podemos derivar la ec. [20aa]:
 [20aa]
Þ
[20aa]
Þ [20aaa]
[20aaa]
Prestando
atención a la ecuación [20aa] vemos que el cociente
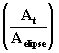 no es otra cosa
sino la expresión en forma de % da área barrida respecto
del área total; pero, M es un ángulo dependiente
del tiempo t, de forma que el producto 2p
.% da un ángulo proporcional al área barrida, o sea al
tiempo t. Esto nos hace pensar en un movimiento circular. En la ec. [20aaa] verificamos
la proporcionalidad entre el tiempo t del movimiento circular y el área
barrida At (pues la velocidad angular es constante en la
circunferencia), o sea, si hablamos de um sector circular barrido en un
tiempo t igual a 25% del período T obtenemos 25% del
área do círculo, entonces el ángulo del sector será
25%.2p
= p/4 radianes o 25%.360
° = 90°
. Estas consideraciones nos llevan a pensar que tal vez M esté
relacionado con algún tipo de circunferencia auxiliar; o sea, la
órbita es circular y la velocidade angular es constante. Cuando
tratemos la Ecuación de Kepler veremos que esta idea
es absolutamente válida.
no es otra cosa
sino la expresión en forma de % da área barrida respecto
del área total; pero, M es un ángulo dependiente
del tiempo t, de forma que el producto 2p
.% da un ángulo proporcional al área barrida, o sea al
tiempo t. Esto nos hace pensar en un movimiento circular. En la ec. [20aaa] verificamos
la proporcionalidad entre el tiempo t del movimiento circular y el área
barrida At (pues la velocidad angular es constante en la
circunferencia), o sea, si hablamos de um sector circular barrido en un
tiempo t igual a 25% del período T obtenemos 25% del
área do círculo, entonces el ángulo del sector será
25%.2p
= p/4 radianes o 25%.360
° = 90°
. Estas consideraciones nos llevan a pensar que tal vez M esté
relacionado con algún tipo de circunferencia auxiliar; o sea, la
órbita es circular y la velocidade angular es constante. Cuando
tratemos la Ecuación de Kepler veremos que esta idea
es absolutamente válida.
Analicemos ahora las dimensiones de la constante
L/m. El momento de la cantidad de movimiento [L] tiene
la dimensión { }, la
masa [m] ={
}, la
masa [m] ={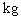 }, de forma que la
dimensión del cociente {L/m} es {m2/s}, que
multiplicado por el tiempo t nos da una superficie. Esto resulta
bastante claro si observamos el miembro derecho de la ecuación [14], donde el
único factor no adimensional es el semi-eje mayor de la órbita
a elevado al cuadrado. Claro que poco interesa si a está
en metros o unidades astronómicas, la superficie será siempre
{m2} o {ua2}.
}, de forma que la
dimensión del cociente {L/m} es {m2/s}, que
multiplicado por el tiempo t nos da una superficie. Esto resulta
bastante claro si observamos el miembro derecho de la ecuación [14], donde el
único factor no adimensional es el semi-eje mayor de la órbita
a elevado al cuadrado. Claro que poco interesa si a está
en metros o unidades astronómicas, la superficie será siempre
{m2} o {ua2}.
Examinando ahora la ecuación de Kepler, sea en la forma dada por la ecuación [17], según la cual:
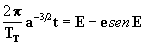 , o en la forma dada
por la ecuación [20], según la cual: M = E - sen
(E) , vemos que no existe factor dimensional, excepto el valor 2
p
, que está expresado en radianes, o como ya vimos antes, en grafos
sexagesimales (no olvidemos que para operar en el lado direcho de la expresión
debemos trabajar en radianes!).
, o en la forma dada
por la ecuación [20], según la cual: M = E - sen
(E) , vemos que no existe factor dimensional, excepto el valor 2
p
, que está expresado en radianes, o como ya vimos antes, en grafos
sexagesimales (no olvidemos que para operar en el lado direcho de la expresión
debemos trabajar en radianes!).
Es interesante entender el significado de la constante de Gauss:
Igualemos la ec. [14]:
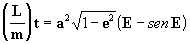 , con la [20]: n
Dt = E - sen(E), para
esto tomamos l ec. [14] y despejamos E - sen(E), de modo que
ahora tenemos:
, con la [20]: n
Dt = E - sen(E), para
esto tomamos l ec. [14] y despejamos E - sen(E), de modo que
ahora tenemos:
E - sen(E) = 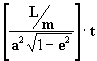
comparando esta última con la ec. [20] llegamos a:
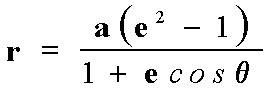
o sea:
 [21]
[21]
pero de la ec. [8 a]: 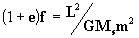 deducimos que :
deducimos que :
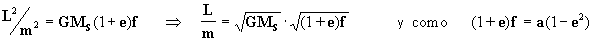
entonces:
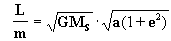 , de forma que introduciendo este valor
en la ecuación [21] tenemos:
, de forma que introduciendo este valor
en la ecuación [21] tenemos:

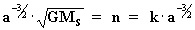 [22]
[22]
 [23]
[23]
por otro lado, de la ecuación [10]:
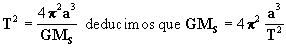 de forma que tenemos:
de forma que tenemos:
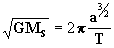 , por lo tanto la
ecuación [22] del movimiento diurno medio queda
de la siguiente forma:
, por lo tanto la
ecuación [22] del movimiento diurno medio queda
de la siguiente forma:
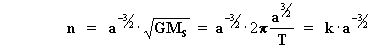
o sea:  [24]
[24]
de lo cual:
 [25]
[25]
así, una manera de encontrar k y utilizar los valores de a y T terrestres, de forma que si a = 1 ua, e T = TT, (atención que para cualquier otro planeta, k se calcula por la [25]),entonces:
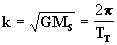 [26]
[26]
tal como fue hecho en la [18a] cuando introducimos la constante de Gauss.
Calculemos entonces el valor de k de acuerdo con la ec. [23], para esto debemos pasar las unidades de [G]
= {
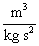 } para {
} para {
 }, o sea que si G [
}, o sea que si G [
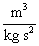 ] = 6.67 10-11
] = 6.67 10-11
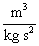 entonces:
entonces:
G [
 ] = 6.67 10-11
] = 6.67 10-11
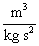 (1 ua/1.495979 1011 m)
3 (86400 s/día)2 =
(1 ua/1.495979 1011 m)
3 (86400 s/día)2 =
G [
 ] = 1.4872 10-34
] = 1.4872 10-34

y como MS = 1.991 1030 kg
entonces: Þk =
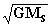 = 0.0172076
» 0.0172
= 0.0172076
» 0.0172
que concuerda con el valor introducido per la ecuación [26] pues:
 =
2p / 365.2564 dia = 0.017202
=
2p / 365.2564 dia = 0.017202
Resumiendo:
 ), que resulta
de imaginar su órbita como circular, de forma que
), que resulta
de imaginar su órbita como circular, de forma que
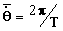 .
.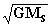
Cuando resolvemos la ecuación [12], introducimos el
parámetro E tal que se cumplía la relación dada por la
ecuación [12a] :  .
Resta saber ahora qué significa la ec. [12a] .
.
Resta saber ahora qué significa la ec. [12a] .
Veamos la Figura 6:
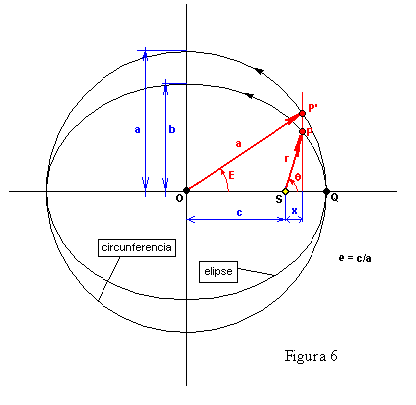
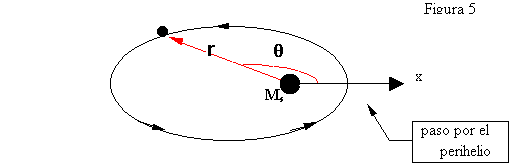
En esta figura observamos al sol, dado por el punto S, la posición del planeta, dada por el punto P, en su órbita elíptica de perihelio SQ¸excentricidad e, y dimensiones orbitales a y b. Ahora trazamos uma órbita circular de radio a y centro O, que obviamente no coincide con S, en esta órbita circular hay um planeta imaginario, de idênticas características a P, denominado P’. Este planeta P’ tiene el mismo período orbital T que P pero se mueve con velocidad angular uniforme (pues la órbita es circular). Resulta evidente que la velocidad angular del planeta P’ vale 2p /T, pero esto no es otra cosa sino el movimiento diurno medio del planeta P.
La posición del planeta P en coordenadas polares de centro S está definida por la anomalía verdadera (q ), y el radio vector (r). La posición del planeta P en coordenadas polares de centro O(excéntrico respecto de S) está definida por la anomalía excéntrica (E), y el radio vector (a).
Vamos a demostrar ahora la correspondencia
entre las posiciones de P y P’ tal como mostradas en la Figura 6.
Analizando la figura observamos que la componente horizontal del radio vector a de
P’, vale acosE. Este valor es igual a la
distancia c + x, pero c = ae, y x = rcos
q. Recordando que r vale
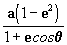 (elipse con el centro de coordenadas
polares centrado en el foco derecho), entonces podemos decir que:
(elipse con el centro de coordenadas
polares centrado en el foco derecho), entonces podemos decir que:
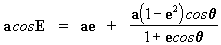 . Después de operar en esta
igualdad podemos encontrar el valor de cosE, o sea:
. Después de operar en esta
igualdad podemos encontrar el valor de cosE, o sea:
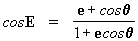 [27]
[27]
Recordando las
funciones trigonométricas que
 , podemos introducir la
ecuación [27] en esta última, de forma que:
, podemos introducir la
ecuación [27] en esta última, de forma que:
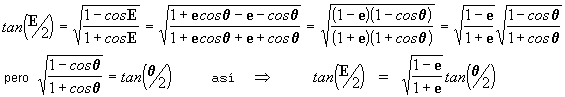
que es precisamente la ecuación [12a], tal como queríamos demontrar. Ahora sabemos el significado real del concepto anomalía excéntrica.
8. CÁLCULO DE ÓRBITAS NO ELÍPTICAS: ÓRBITAS PARABÓLICAS E HIPERBÓLICAS
Cuando llegamos a la ecuación [8aa] que nos daba la fórmula general de la cónica, continuamos nuestro razonamiento asumiendo que 0 < e < 1, así, para llegar a la ecuación de Kepler, introducimos el valor de r en el cálculo de la integral dada por la ecuación [11]. Para el caso de las órbitas parabólicas, sabemos que e = 1, pero rahagamos la integración de la [11] considerando la ecuación de la parábola (que resulta de introducir e=1 en la ec. [8aa]).
Veamos la Figura 7: la distancia focal
SQ del sol durante el paso por el perihelio fue denominada f;
la excentricidad de la elipse vale e = 1, colocando estos
datos en la ecuación [8aa]: 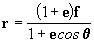 ,
llegamos a la ecuación de la órbita parabólica:
,
llegamos a la ecuación de la órbita parabólica:
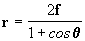 . Ahora, apenas por uma cuestión
de nomenclatura, denominamos a la distancia focal f de q,
o sea q = f.
. Ahora, apenas por uma cuestión
de nomenclatura, denominamos a la distancia focal f de q,
o sea q = f.
Por lo tanto la ecuación de la parábola é:
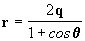 [28]
[28]
Ahora vamos
a hacer la integración:  ,
introducindo el valor de r dado por la ec. [28].
,
introducindo el valor de r dado por la ec. [28].
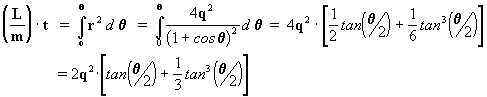
pero como

entonces:
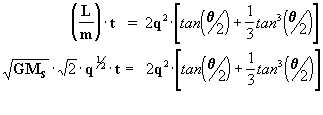
despejando ahora el término de las tangentes:
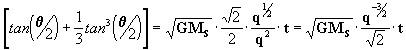
o sea que:
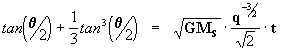 [29]
[29]
ecuación análoga a [17] en el sentido que en su resolución obtenemos el valor de q.
En este caso tenemos que resolver uma ecuación cúbica en tan(q/2). Se puede demostrar que esta ecuación tiene una raíz real (la que nos interesa) y dos imaginarias. Existen bastantes métodos de resolución. Proponemos el Método de Newton, que dice: Si x0 es un valor aproximado de la raíz de la función f(x)=0 entonces como aproximación más exacta se toma
 Sustituyendo ahora x1 por x0 obtenemos
una mejor aproximación x2.
Sustituyendo ahora x1 por x0 obtenemos
una mejor aproximación x2.
Así, para nuestro problema (resolución de la ecuación [29]):
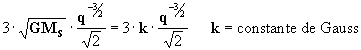
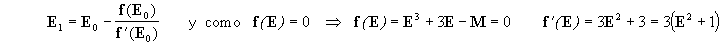
luego: 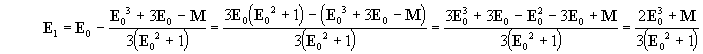
o sea
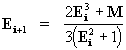 [29a]
[29a]
Este valor será iterado hasta que f( Ei ) » 0 , por ejemplo hasta que ½ f( Ei ) ½ = 10-8.
En este caso se procede como en el anterior, recordando que si e
> 1 entonces  pues según la
definición en la hipérbola, c > a Þ
f = c - a Þ
(1+e)f = (1+e)(e-1)a = a(e2-1), luego:
pues según la
definición en la hipérbola, c > a Þ
f = c - a Þ
(1+e)f = (1+e)(e-1)a = a(e2-1), luego:

entonces:

Vamos ahora a hacer algunas consideraciones al respecto de las funciones trigonométricas hiperbólicas, para esto tomamos el fator dentro do logaritmo natural en la ecuación [30]:
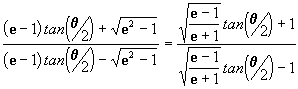 y si
y si

entonces tenemos que:


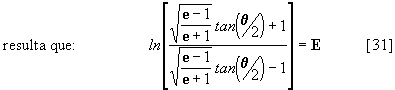
podemos ahora calcular el valor de senh(E), o sea:

luego se deduce que
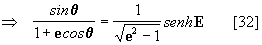
así, introduciendo las ecuaciones [31] y [32] en la ecuación [30] obtenemos:

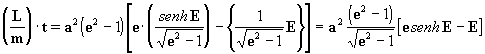
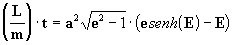 [33]
[33]
recordando ahora que en la ecuación general de las cónicas [8], el numerador representa el parámetro p que vale (1+e)f, entonces de acuerdo a la ec. [8a] obtenemos, como principio general para las órbitas cónicas:

pero en la definición inicial de hipérbola habíamos visto que
 , o sea que:
, o sea que:

de forma que introduciendo la ec. [34] en la ecuación [33]:
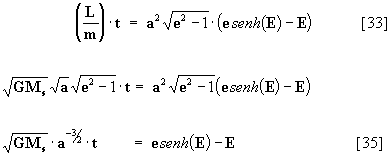

y como a = q / (e-1) para la hipérbola, entonces la ec. [35]:
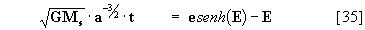
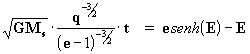 [36]
[36]
Ecuación parecida a la obtenida en el cálculo de las órbitas elípticas, en este caso la resolución de la ec. [36] es idéntico al de la ecuación [17] o [20], o sea:
E = e senh(E) - M
M = n.t
n = 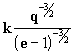 donde
donde