 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|
Caveat Emptor
|
|
|
 |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
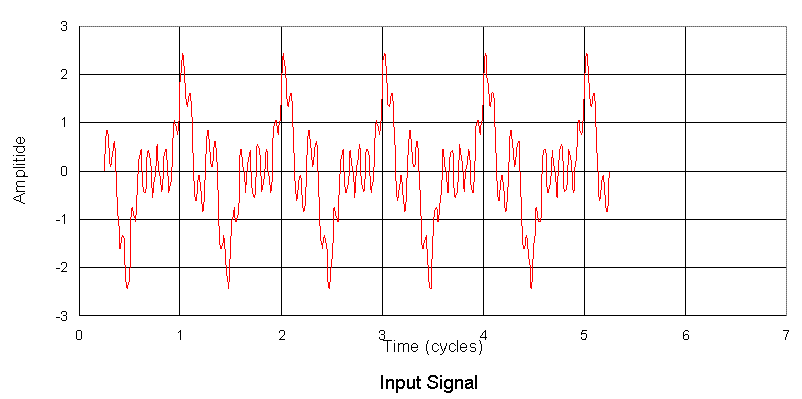
On the previous page the characteristis of sealed box woofer systems wre discussed with regard to the reproduction of a single tone near the resonant frequency of the system. However, we seldom listen to a single tone, except perhaps during testing or when listening to certain types of electronic music. We noted that at resonance the phase of the output was shifted 90 degrees relative to the input. We also recognize that the phase shifts introduced vary with frequency. So perhaps we should also look at a more complex signal composed of a fundamental and several other frequencies, be they harmonics or otherwise. How does the system Q affect the ability of the system to accurately reproduce this more complex, multi-toned signal? Obviously both amplitude and phase will play a roll in determining the characteristic of the output. The figure below show the input signal I concocted to test the ability of the systems to track a complex signal. The signal is composed of a fundamental and a number of harmonically related frequencies. |
|
|
|
 |
|
|
|
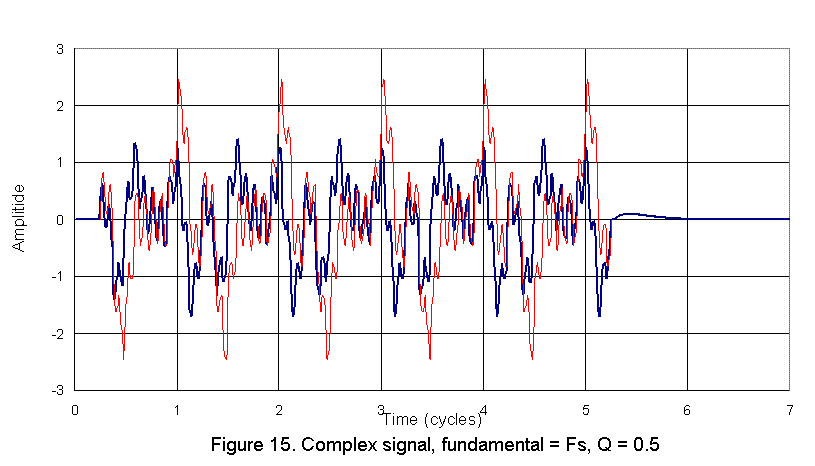
In Figure 15, below, a comparison between the input (red) and output (blue) for a Q = 0.5 system is shown. In this case the fundamental of the input signal is equal to the system resonant frequency. The output is hardly recognizible as being related to the input. Never the less, this is what the acoustic output of the system would be for the given input signal. I offer no comments on the audibility of this distortion of the input signal, but it is clear that the output is not an accurate reproduction of the input. |
|
|
|
 |
|
|
|
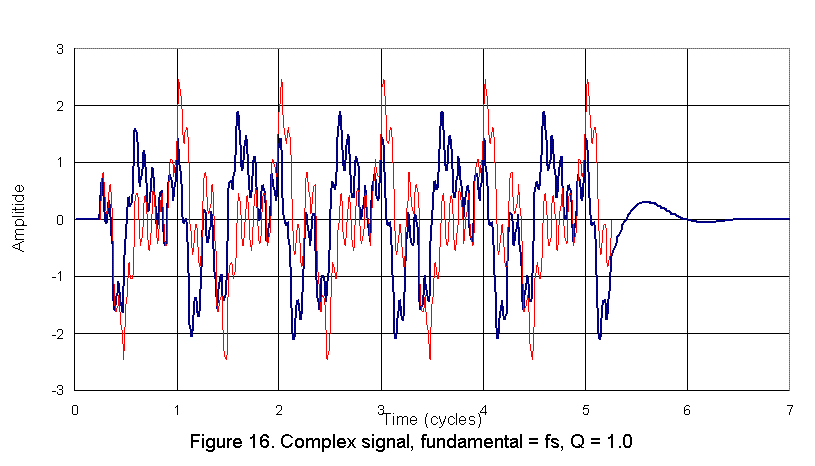
The next figure, Figure 16, shows a similar result for a Q = 1.0 system. The accuracy of the reproduction can hardly be be considered any better than the Q= 0.5 system with the possible exception that the peak amplitudes are more closely related to the peak amplitudes of the input signal. |
|
|
|
 |
|
|
|
The distortion in the output wave form compared to the input signal in the two cases above is related to both the amplitude and phase response of each system. As was shown on the previous page of the discussion, for frequencies at and above the system resonance the Q = 1.0 system introduce little amplitude distortion. Thus the Q = 1.0 result of Figure 16 reflects mainly phase distortion. The Q = 0.5 result, on the other hand, reflects both phase and amplitude distortion due to the reduced amplitude at and around the system resonance. Still it is reasonable to ask for each system, how far above the system resonance would the the fundamental of the input signal need to be before neither the phase nor amplitude distortion associtaed with the woofer system high pass characteristic resulted in significant loss of accuracy in the output.
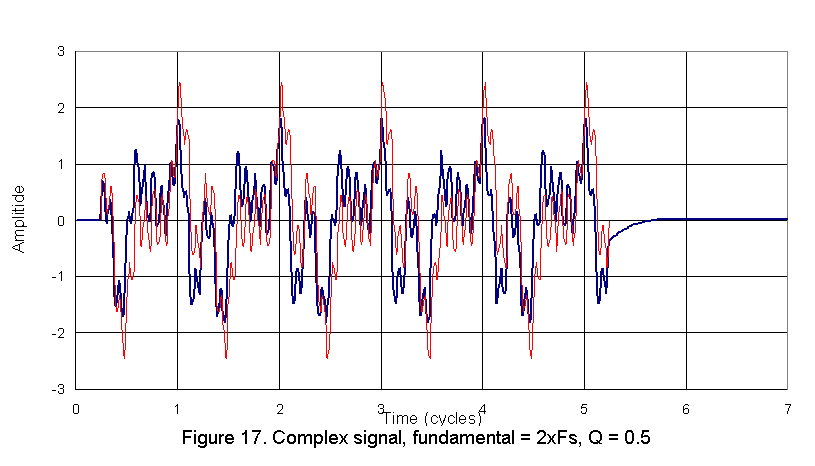
Figure 17 shows a comparison between the input and output for the Q = 0.5 system when the fundamental of the input is an octave above the system resonances. There is clearly an improvement in the response but significant departure from the input is still apparent. |
|
|
|
 |
|
|
|
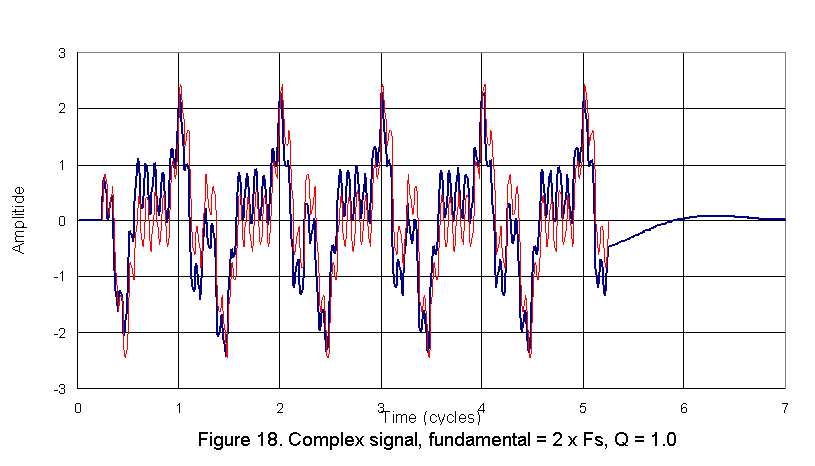
Figure 18 shows the same comparison between the input and output for the Q = 1.0 system. This system shows even more improvement but there are still obvious discrepancies. The problem is that as soon as any high pass characteristic is introduced between the input and the output, other than one which has a linear or zero phase shif characteristic, there will be some degree of frequency dependent phase distrotion introduced between the input and output, even in the region above resonance where the amplitude response is nearly perfectly flat. The further the fundamental of the input signal is above the high pass system resonance, the lower the level of phase distortion, but it can never be completely eliminated. From this point of view, it would be desirable to build a woofer system with Fs well below the lowest frequency the system is asked to reproduce. However, this is contradictory to the consideration of room gain effects unless the room is suitable large. Overall what we see here is how difficult it really is to produce a woofer system in any environment that will accurately reproduce an input with low frequency content. It's no wonder the bass is never right. |
|
|
|
 |
|