Analisas Berstatistik Asas
6.1
Pengertian dan Pengunaan Statistik
Statistik ialah satu jenis
analisis data yang mengamalkan perancangan, rumusan, dan mengintrepretasikan
sistem pemerhatian yang meramalkan kejadian berdasarkan pengiraan system model
matematik yang diperhatikan. Statistik adalah cabang matematik gunaan
yang menumpukan kepada teori
kebarangkalian. Implikasi teori kebarangkalian ini adalah hasilan keputusan statistik yang dapat
menunjukkan hubungan korelasi
Perihal statistik yang asas adalah populasi boleh
diwakili melalui satu set sampel
populasi yang mana sampel tersebut adalah agak besar . Teori statistik
menyediakan kaedah bagi menentukan
besar manakah sampel yang diperlukan untuk menyediakan keperluan hasilan keputusan yang signifikan.
Dua jenis statistik asas ialah statistik deskriptif dan
statistik inferensi. Statistik deskriptif menerangkan atau merumuskan sistem
pemerhatian pengkuran. Sementara deskriptif inferensi digunakan untuk meramal atau membuat agakan
kepada sifat sistem.
Statistik digunakan meluas dalam dpelbagai disiplin
terutama bidang sains sosial , kajihayat dan lain-lain bidang pembelajaran yang
melibatkan sistem yang kompleks. Statistik digunakan juga dalam perniagaan bagi
tujuan pengawalan proses, pengawalan mutu,
pemasaran dan lain-alain aktiviti harian. Dalam bidang sukan, statistik
digunakan untuk memaklumkan
kemahiran dan kebolehan ahli sukan. Sektor kerajaan menggunakan statitistik
dalam pelbagai hal,terutama dalam kerja bancian mengenai populasi penduduk.
Objektif
Di
akhir bab ini, anda seharusnya dapat :
1.
memahami asas kefahaman mengenai menginterepretasikan
mengenai statistic deskriptif dan inferen
2.
memahami konsep asas ukuran kekerapan, taburan dan serakan
6.1.1
Pengertian Statistik
Statistik adalah
kaedah mudah untuk membuat pengukuran dan memaklumkan perhubungan dengan
mengunakan nombor.
Kebanyakan kekeliruan awal ketika mempelajari statistics
adalah tidak memahami konsep dan istilah. Apabila mengunakkan kaedah
statistic, kita boleh mengunakan pelbagai istilah untuk menerangkan konsep.
Jika anda ingin menerangkan mengenai perbatuan pengunaan minyak kenderaan anda,
pernyataan seperti dibawah boleh digunakan :
·
Tangki minyak kenderaan saya sudah penuh
·
Tangki minyak kenderaan saya hanya tinggal separuh
·
Aras tingki
minyak saya adalah pada kadar 50%
·
Kenderaan saya hanya mampu bergerak sejauh 150 kilometer
Semua pernyataan ini menerangkan kadar pengunaan minyak kenderaan anda. Dari
maklumat ini anda boleh membuat keputusan bila anda perlu membeli minyak.
Dari kenyataan ini
anda boleh membuat pengiraan mudah dan pastinya anda tahu bahawa purata pergerakan kenderaan anda adalah
diantara tujuhbelas hingga 35 batu segelen.
Dalam menyatakan kaedah skoran yang digunakan
didalam pengukuran dan penilaian anda boleh mengunakan kenyataan seperti diatas :
·
Skoran persamaan umur
·
Skoran persamaan gred
·
Skoran piawai dan sisihan piawai
·
Ranking persentil
Pengetahuan mengenai statistic akan membolehkan anda menilai pencapaian pelajaran anak-anak
anda.

Mana-mana analisa statistik
bermula dari masalah, satu adalah yang anda cari dan atau yang anda diberi.
"pelajar yang belajar lebih tahu lebih "
 Jika anda mempunyai dua kumpulan
pelajar, anda boleh mengasingkan dua kumpulan tersebut dalam dua kumpulan. Kumpulan
pertama belajar secukupnya dan sekumpulan lagi diminta datau digalakkan untuk
belajar, katakanlah dua kali lebih lama. Oleh itu, anda bolehlah melakukan perkara berikut:
Jika anda mempunyai dua kumpulan
pelajar, anda boleh mengasingkan dua kumpulan tersebut dalam dua kumpulan. Kumpulan
pertama belajar secukupnya dan sekumpulan lagi diminta datau digalakkan untuk
belajar, katakanlah dua kali lebih lama. Oleh itu, anda bolehlah melakukan perkara berikut:
-
Dua benda berlainan? – bandingkan
purata skor pembelajaran bagi kedua-dua kumpulan tersebut
- Satu
langkah lagi adalah mengukur banyak manakah yang dipelajari atau masa
pelajar belajar
oleh kedua kumpulan tersebut. Anda boleh bertanya kepada
pelajar tersebut tetapi kaedah tersebut bolehkah dipercayai Maka anda boleh menggunakan kaedah :
- Dua perkara berkaitan? –
perhatikan
perhubungan diantara banyak mana yang dipelajari dan masa yang digunakan
untuk belajar. Untuk ini, anda boleh menggunakan kaedah statistic yang
ditnjukkan pada jadual , kemungkinan ‘R” yang
bermaksud korelasi koefisen Pearson.
6.1.2
Pengunaan Statistik dalam Pendidikan
Pengukuran ialah suatu proses atau
sistem yang digunakan untuk menentukan nilai
kuantitatif sesuatu benda, perkara atau keadaan. Nilai
kuantitatif ini biasanya dinyatakan dalam
sesuatu unit angka yang tetap dengan menggunakan alat pengukuran yang
berkaitan.
Dalam proses pengajaran dan
pembelajaran, pengukuran merangkumi segala aspek pengujian, termasuk menggunakan skala ordinal atau skala
selang untuk menentukan kedudukan
dan pencapaian pelajar-pelajar dalam sesebuah kelas atau di antara kelas. Skala ordinal ini
merupakan sesuatu alat pengukuran yang digunakan untuk menempatkan pangkatan
atau kedudukan pelajar-pelajar mengikut markah-markah yang diperolehi daripada
sesuatu ujian. Skala selang yang mengandungi unit markah-markah yang sama berat nilainya, adalah digunakan bukan sahaja untuk
menentukan pangkatan, tetapi juga membuat perbandingan di antara
pelajar-pelajar dalam sesebuah kelas yang sama ataupun di antara kelas-kelas
yang lain. Secara ringkasnya, skala ordinal digunakan berdasarkan prestasi atau pencapaian mereka.
Skala selang, yang meliputi markah dan gred, digunakan untuk menentukan
peringkat pencapaian di antara pelajar.
Mcnamara (1998), menyatakan
pengukuran ialah suatu penyiasatan tentang kualiti sesuatu proses penilaian dengan melihat skor pencapaian.
Berdasarkan ini beliau menegaskan bahawa terdapat dua langkah untuk membuat
pengukuran:
- Mengkuantitikan- iaitu menetapkan nombor atau
skor untuk berbagai-bagai hasil penilaian. Satu set skor boleh digunakan
untuk membuat analisis data himpunan daripada perolehan nombor yang
diambil daripada dapatan ujian yang dinamakan data matrik.
- Semakan- iaitu membuat semakan menggunakan
berbagai jenis dan bentuk pengiraan secara matematik dan statistik dlam
membuat penilaian perkara-perkara yang penting (seperti ketekalan
persembahan calon atau penilai)yang akan mempengaruhi penilaian.
Sebab utama langkah ini dibuat adalah untuk mencapai tahap kualiti
kontrol, yang bertujuan untuk meningkatkan lagi tahap kebolehpercayaan dan
keadilan pada keputusan yang diperolehi tentang seseorang calon (kesahihan
ujian). Prosedur untuk membuat pengukuran bukan sahaja perlu rasional malah
dapat menguatkan kesahihan ujian. Di sini jelaslah bahawa sesuatu pengukuran itu perlulah
mempunyai ciri-ciri seperti kesahan, kebolehpercayaan, linearity, praktikal, ketunggalan atau keobjektifan dan kemudahtafsiran
untuk memudahkan hasil ujian calon direkodkan supaya tidak timbul sebarang rasa
tidak percaya terhadap hasil pengukuran itu kelak.
Terdapat beberapa penggunaan statistic dalam pengukuran yang melibatkan pelbagai
symbol atau pernomboran perhubungan dan operasi membuat pengukuran. Tahap yang sering diperbincangkan
dalam hal ini adalah :
Taraf Nominal
Pengukuran data yang paling rendah
adalah taraf nominal. Nombor
mewakili data taraf nominal boleh digunakan hanya untuk pengelasan dan
kategori. Nombor
pengenalan kakitangan adalah sebagai contoh data nominal. Nombor yang digunakan
hanyalah untuk membezakan kakitangan dan bukanlah untuk memberikan pernyataan
nilai terhadap mereka. Banyak soalan-soalan demografi di dalam survei adalah data nominal
disebabkan soalan yang digunakan hanyalah untuk pengelasan sahaja. Contoh soalan seperti tersebut adalah:
Manakah klasifikasi pekerjaan yang terbaik menerangkan bidang kerja
anda?
A.
Pendidik
B.
Pekerjaan binaan
C.
Pekerja Perkilangan
D.
Peguam
E.
Doktor
F.
Lain-lain
Oleh yang demikian, untuk tujuan
pengiraan, pendidik ditandakan sebagai 1, pekerjaan binaan sebagai 2, pekerja
perkilangan sebagai 3, dan seterusnya. Nombor hanyalah digunakan untuk mengkelaskan pekerja sahaja. Nombor 1 bukan menandakan
pengkelasan tertinggi. Ia hanya bertujuan untuk membezakan di antara pendidik (1)
dan doktor (5). Lain-lain
data demografi seperti bangsa, jantina, tempat tinggal dan lain-lain merupakan
data bertaraf nominal.
Taraf
Ordinal
Pengukuran data bertaraf ordinal
adalah lebih tinggi daripada nominal. Disamping
itu, data ordinal boleh digunakan untuk memeringkatkan atau menyusun objek. Sebagai contoh, dengan
menggunakan data ordinal, penyelia boleh menilai tiga orang pekerja dengan
memeringkatkan produktiviti mereka dengan nombor 1 hingga 3. Penyelia boleh
mengenalpasti, satu pekerja amat produktif, saorang pekerja kurang produktif
dan saorang lagi tidak produktif menggunakan data ordinal. Walau bagaimanapun, penyelia tidak boleh
menggunakan data ordinal untuk membuktikan interval di antara dua orang pekerja
yang diperingkatkan sebagai 1 dan 2 atau pekerja diperingkat 2 dan 3 adalah
sama. Iaitu, ia
tidak boleh menyatakan bahawa perbezaan di antara oekerja diperingkat 1, 2 dan
3 adalah sama. Dengan data ordinal,
jarak yang diwakili oleh nombor yang berturutan adalah tidak selalunya sama.
Beberapa soalan
soal-selidik jenis skala Likert yang selalu digunakan oleh penyelidik adalah
jenis ordinal. Berikut adalah contoh skala tersebut:
Kualiti perkhidmatan yang diberi oleh Bank di Malaysia adalah baik.
|
Amat
Bersetuju
|
Bersetuju
|
Tidak
Pasti
|
Tidak Bersetuju
|
Amat tidak Bersetuju
|
|
1
|
2
|
3
|
4
|
5
|
Apabila soalan
survei ini dikodkan kedalam komputer, hanya nombor 1 hingga 5 sahaja yang
dimasukkan bukannya keterangannya. Secara maya semua orang bersetuju bahawa
5 lebih tinggi daripada 4 di dalam skala ini dan pemeringkatan tindakbalas
adalah mungkin. Walau
bagaimanapun kebanyakan responden tidak mempertimbangkan perbezaan di antara
Amat Tidak Bersetuju, Tidak Bersetuju, Tidak Pasti, Bersetuju dan Amat
Bersetuju adalah sama.
Sebagai contoh lain, dana pelaburan sebagai pelaburan yang diperingkatkan di dalam
sebutan risiko dengan menggunakan ukuran risiko biasa, risiko kewangan dan
risiko kadar faedah. Tiga
ukuran ini adalah digunakan kepada pelaburan dengan memeringkatkannya sebagai
mempunyai risiko yang tinggi, sederhana dan rendah. Katakan risiko tinggi
ditandakan sebagai 3, sederhana risiko sebagai 2 dan tidak berisiko sebagai 1. Jika dana tersebut
dilabelkan sebagai 3 berbanding 2, ia mempunyai risiko yang lebih dan
seterusnya. Walau bagaimanapun,
perbezaan risiko di antara kategori 1,2 dan 3 tidak semestinya
sama. Oleh itu,
pengukuran risiko ini hanyalah taraf pengukuran ordinal. Disebabkan oleh
data nominal dan ordinal biasanya diterbitkan daripada pengukuran seperti soalan demografi, kategori
manusia atau objek, atau pemeringkatan sesuatu item, data nominal dan ordinal
adalah data bukan metrik atau kadangkala dipanggil sebagai data
kualitatif.
Taraf
Interval
Pengukuran data interval adalah taraf data yang tertinggi sedikit.
Pengukuran interval mempunyai semua kandungan data
taraf ordinal, tetapi jarak di antara nombor berturutan mempunyai makna dan
data selalunya adalah numerik.
Jarak adalah diwakili oleh perbezaan di antara nombor berturutan adalah sama. Contoh pengukuran interval adalah nombor suhu Farenheit, suhu boleh
diperingkatkan, jumlah kepanasan di antara bacaan berturutan, seperti 21o,
22o dan 23o.
Disamping
itu, dengan paras data interval, titik sifar hanyalah
konvension atau keselesaan dan bukan semula jadi atau tetap pada titik
sifar. Oleh itu, sifar hanyalah titik
lain di atas skala dan tidak bermakna ia tidak ujud di
dalam fenomena. Sebagai
contoh, 0o F bukanlan suhu terendah yang mungkin. Contoh lain data
taraf interval adalah peratus perubahan di dalam pekerjaan, peratus pulangan
keatas pelaburan dan perubahan di dalam harga saham.
Dengan data
taraf interval, transformasi unit dari satu pengukuran kepada yang lain
melibatkan pendharaban dengan faktor tertentu,
a, dan
menambah dengan faktor lain,
b, oleh itu Y =
a +
bX. Sebagai contoh, untuk mengubah suhu Calcius
kepada suhu Farenheit melibatkan perhubungan F= 32 + 9/5 C
Taraf
Kadar
Ukuran taraf kadar
adalah taraf pengukuran data yang tertinggi.
Data kadar mempunyai kandungan yang sama
sebagaimana data interval, tetapi data perkadaran mempunyai nilai mutlak sifar
dan kadar bagi dua nombor adalah bermakna.
Notasi nilai mutlak sifar bermakna nilai sifar adalah
tetap dan oleh itu ujud nilai sifar di dalam data yang mewakili ketidakhadiran
ciri-ciri yang dikaji. Nilai
sifar tidak boleh secara arbitrari diletakkan disebabkan ia
mewakili titik tetap. Definasi ini
membolehkan statistik mengujudkan kadar dengan
data.
Contoh data kadar adalah tinggi, berat, jumlah jualan dan
sebagainya. Dengan data kadar, penyelidik boleh menyatakan 180 kg adalah lebih berat
daripada 90 kg atau sebaliknya, dan membuat kadar 180:90.
Disebabkan
oleh data taraf interval dan kadar biasanya diperolehi daripada alatan yang
biasanya digunakan di dalam proses pengeluaran dan proses kejuruteraan, di
dalam ujian piawai kebangsaan, atau tatacara perakaunan piawai, ianya dipanggil
data matrik dan kadangkala dirujukkan sebagai data kuantitatif.
Perbandingan
Empat Taraf data
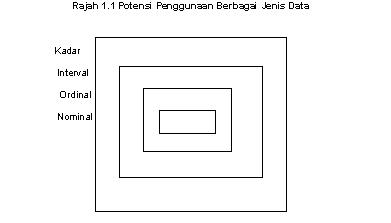
Rajah 1.1 menunjukkan perhubungan potensi penggunaan di antara empat
taraf pengukuran data. Empat persegi yang tertinggi menandakan
setiap kategori paras data boleh dianalisis dengan sebarang teknik
yang digunakan keatas taraf data yang terendah, tetapi sebagai tambahan, boleh
dianalisis menggunakan sebarang teknik statistik yang boleh digunakan terhadap
lain-lain tiga jenis data ditambah dengan yang lain.
Data nominal adalah data yang amat terhad di dalam jenis analisis
staistik yang boleh digunakan dengan mereka.
Data ordinal membolehkan penyelidik untuk melakukan sebarang analisis
yang boleh dilakukan dengan data nominal ditambah dengan yang lain. Melalui data kadar,
ahli-ahli statistik berkebolehan untuk membuat perbandingan pendaraban dan
bersesuaian melakukan sebarang analisis yang boleh dilakukan oleh data nominal,
ordinal atau interval. Sesetengah teknik
statistik memerlukan data kadar dan tidak boleh
digunakan untuk menganalisis lain-lain taraf data.
Teknik statistik boleh digunakan di dalam dua kategori statistik
parametrik dan statistic tidak berparametrik. Statistik parametrik memerlukan
data interval atau kadar. Jika data adalah nominal atau ordinal, statistik
tidak berparameter mesti digunakan.
Statistik tidak berparameter juga boleh digunakan statistik tidak
berparameter juga boleh digunakan untuk menganalisis data interval dan kadar.
6.1.3
Pengunaan Statistik dalam Penilaian
Tujuan utama penilaian dalam bidang
pendidikan dan psikologi ialah untuk mendapatkan langkah-langkah yang objektif serta boleh difahami dalam bentuk
perbandingan yang mutlak. Kenyataan berikut merangkumi seluruh
interpretasi bagi data ujian dan bukan ujian. Data ujian hanyalah
merupakan salah satu cara bagi mendapatkan maklumat
dalam membimbing ahli memilih sesuatu keputusandalamprosesbimbingan/kaunseling.
1. Ahli mestilah menerangkan dengan khusus maklumat mengenai ujian, sebelum dan selepas ujian dibuat supaya
keputusan ujian itu dapat diterima dalam perspektif yang betul jika dikaitkan dengan
faktor-faktor sosio-ekonomi, bangsa dan budaya
dalam pencapaian ujian itu.
2. Dalam memilih ujian untuk digunakan dalam satu-satu situasi bagi seseorang
klien, ahli harus
menimbang dengan teliti mengenai kesahan dan kebolehpercayaan serta kesesuaian atau ketepatan ujian itu.
3. Ujian yang berlainan memerlukan tahap kelayakan pengendalian yang berbeza
dan interpretasi yang berlainan. Ahli mestilah menyedari had-had kebolehan
sendiri dan menjalankan hanya tugas-tugas yang ia
layak sahaja.
4. Tujuan ujian dan kegunaan keputusan hendaklah diberitahu kepada calon-calon sebelum ujian
diberi.
5. Bila membuat kenyataan kepada orang awam mengenai ujian dan pengujian, ahli
mestilah memberi keterangan yang tepat dan mengelak dari membuat dakwaan
yang tidak benar atau tanggapan yang salah.
6.
Ujian-ujian mestilah dijalankan dalam keadaan-keadaan yang sama
seperti norma. Bila ujian tidak dijalankan dalam
keadaan-keadaan yang lazim atau bila berlakunya sesuatu tingkahlaku,
perkara itu mestilah dicatatkan. Keputusan-keputusan ujian berkenaan hendaklah
diisytiharkan sebagai tidak sah atau yang boleh meragukan.
7. Pencapai
yang bererti dari keputuan ujian-ujian yang digunakan oleh kaunselor lazimnya berdasarkan ketidakbiasaan calon mengenai
perkara tertentu yang terdekat dalam ujian itu, mengajar atau memberitahu
bahan-bahan ujian sebelum sesuatu ujian dijalankan memungkinkan keputusannya
tidak sah. Oleh itu pengawasan rapi ujian adalahsalah satu
daripada tanggungjawab ahli.
8. Ahli
mestilah berhati-hati apabila menginterpretasi sesuatu keputusan dari bahan
atau alat kajian yang tidak lengkap. Tujuan utama penggunaan
alat kajian itu mestilah dinyatakan dengan jelas kepada calon.
9. Keputusan ujian yang diberi kepada majikan atau lain-lain pihak yang
berkenaan untuk tujuan penilaian atau
klasifikasi harus diawasi supaya tidak disalah erti atau disalah
guna. Kebajikan calon ujian harus diambilkira sebagai satu kriteria penting dalam
apa-apa pertimbangan.
10. Ahli
mestilah berhati-hati apabila membuat penilaian dan menginterpretasi restasi mereka
yang
tidak termasuk di dalam golongan norma semasa alat ujian itu distandardisasikan. Ahli yang
mengguna ujian yang diambil dari luar negeri haruslah berhati-hati semasa menguna
dan
menginterpretasi dengan memikirkan budaya golongan
norma yang telah digunakan oleh pencipta ujian
dalam proses piawaian.
11. Ahli mestilah berhati-hati supaya tidak mencedok, mengubahsuai dan
menggunakan ujian-ujian yang
diterbitkan tanpa menyatakan penghargaan atau
mendapat kebenaran dari penerbit.
6.2
Analisis Kekerapan dan Taburan
Perkara yang perlu difikirkan selepas data mentah dikumpul ialah untuk
membentangkan data tersebut kedalam bentuk yang mudah difahami untuk dibuat
sebarang analisis dan perbandingan. Data mentah yang dikumpulkan tidak dapat memberikan
sebarang makna jika data itu tidak dibentang dalam bentuk grafik ataupun bentuk
lain yang senang dilihat dan ditafsirkan.
Sebagai contoh, data-data kehadiran pelajar tidak memberi sebarang makna
kepada seorang guru jika data tidak dapat dibentangkan dalam bentuk jadual
kekerapan untuk menunjukkan jumlah kehadiran pelajar yang beliau ajar. Pembentangn data
secara graf boleh menunjukkan pergerakan kehadiran murid atau pelajar beliau di
sepanjang masa untuk sesuatu tempoh. Dengan cara
ini pihak sekolah akan lebih faham tentang keadaan kehadiran dan pergerakan
kehadiran pada sesuatu masa yang tertentu.
Oleh sebab
data mentah yang dikumpulkan tidak dapat memberikan sebarang makna kepada
pembaca, kaedah-kaedah seperti jadual kekerapan, polygon kekerapan, ogif carta
pai, carta palang dan lain-lain harus digunakan untuk memberi lebih makna dalam
penyampaian
6.2.1
Analisis Kekerapan dan Grafik
Kaedah yang
paling mudah untuk membentangkan data metah ialah dengan membina sebuah jadual kekerapan . Dua factor yang perlu
dipertimbangkan semasa membina suatu jadual kekerapan ialah bilangan kelas yang
perlu digunakan dan selang bagi setiap kelas. Untuk menentukan bilangan
kelas yang diperlu disediakan, formula berikut selalunya digunakan
:

Taburan
Kekerapan
Taburan kekerapan adalah mudah untuk dibina.
Walaupun terdapat beberapa garis panduan
untuk pembinaannya, taburan adalah berbeza di dalam rekabentuknya, walaupun
data mentah yang awal adalah sama. Sebenarnya taburan kekerapan yang dibina
adalah menurut citarasa penyelidik.Langkah-langkah di dalam membina taburan
kekerapan:
Langkah 1: Tentukan
jeda data mentah tersebut.
Jeda
didefinasikan sebagai perbezaan di antara angka terbesar dan terkecil di dalam
set data. Jeda bagi
data di dalam jadual 2.1 ialah 11.3 (12.5 – 1.2).

Langkah 2: Tenentukan
berapa banyak kelas yang perlu dibina.
Peraturan biasa adalah memilih di antara 5 hingga 15 kelas.
Jika taburan kekerapan mempunyai terlalu sedikit kelas, ringkasan data
adalah terlalu am untuk digunakan. Terlalu banyak kelas pula menghasilkan taburan kekerapan yang tidak
dapat mengumpulkan data secukupnya untuk membantu kita membuat keputusan. Bilangan kelas terakhir
adalah arbitrari. Data di dalam
Jadual 2.1 akan dikumpulkan ke dalam enam kelas
sebagaimana ditunjukkan di dalam Jadual 2.2.
Langkah 3: Tentukan luas jeda kelas.
Penghampiran luas kelas boleh dikira dengan membahagikan
jeda dengan bilangan kelas. Bagi
data di dalam Jadual 2.1, penghampiranya ialah 11.3/4 atau 1.9. Biasanya, nombor tersebut
dibundarkan kepada nombor bulat berikutnya dan di dalam kes ini ialah 2. Taburan kekerapan mesti bermula dengan nilai
yang sama atau lebih rendah daripada nombor terkecil
bagi set data dan berakhir dengan nilai yang sama atau lebih besar daripada
nilai terbesar. Harga
yang terendah ialah 1.2 dan tertinggi 12.5, oleh itu kita boleh memulakan taburan
kekerapan dengan 1 dan berakhir dengan 13. Jadual 2.2 mengandungi
taburan kekerapan lengkap bagi data di dalam Jadual 2.1. Titik akhir kelas adalah
dipilih supaya tiada nilai data yang boleh dimasukkan di dalam lebih dari satu
kelas. Pernyataan
jeda kelas –di bawah – di dalam taburan Jadual 2.2 boleh mengatasi masalah
tersebut.
Titik Tengah Kelas
Titik tengah setiap jeda kelas dipanggil sebagai titik tengah kelas
dan kadangkala dipanggil sebagai tanda kelas.
Ia merupakan nilai pertengahan bagi jeda kelas
dan dikira sebagai purata dua titik akhir kelas. Sebagai contoh, bagi taburan di dalam Jadual
2.2, titik tengah jeda kelas 3-di bawah 5 ialah 4, atau  . Cara
kedua untuk memperolehi titik tengah kelas ialah dengan mengira separuh jarak
disepanjang jeda kelas (separuh dari luas kelas) dan ditambah dengan titik awal
kelas.
. Cara
kedua untuk memperolehi titik tengah kelas ialah dengan mengira separuh jarak
disepanjang jeda kelas (separuh dari luas kelas) dan ditambah dengan titik awal
kelas.
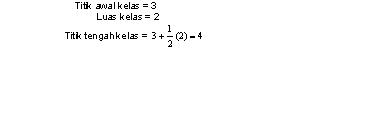
Titik tengah
kelas adalah penting kerana ia mewakili nilai bagi
setiap kelas di dalam kebanyakkan
pengiraan statistik kumpulan. Lajur
ketiga di dalam Jadual 2.3 mengandungi
titik tengah bagi semua kelas bagi data di dalam Jadual 2

Kekerapan
Relatif
Kekerapan relatif ialah bahagian
jumlah kekerapan bagi jeda kelas di dalam taburan kekerapan.
Kekerapan relatif adalah kekerapan kelas individu
dibahagi dengan jumlah kekerapan. Sebagai
contoh, daripada Jadual 2.3,
kekerapan relatif bagi
selang kelas 5-di bawah 7 ialah 4/40, atau 0.10.
Lajur keempat Jadual 2.3
adalah senarai kekerapan relatif bagi taburan kekerapan Jadual 2.2.
Kekerapan
Terkumpul
Kekerapan
terkumpul ialah jumlah kekerapan disepanjang taburan kekerapan.
Kekerapan terkumpul bagi setiap jeda kelas ialah
kekerapan bagi kelas tersebut ditambah dengan jumlah terkumpul jeda sebelumnya. Di dalam Jadual 2.3, kekerapan terkumpul bagi
kelas pertama adalah sama sebagaimana kekerapan kelas,
iaitu 16. Kekerapan
terkumpul bagi jeda kelas kedua ialah kekerapan kelas kedua (2), ditambah
dengan kekerapan terkumpul selang kelas pertama (16), menghasilkan kekerapan
terkumpul yang baru, 2 + 16 = 18. Proses ini berterusan sehingga ke kelas yang
terakhir dimana kekerapan terkumpul adalah sama
sebagaimana jumlah kekerapan, 40. Konsep kekerapan terkumpul digunakan dengan meluas didalam
bidang seperti jualan terkumpul disepanjang
tahun kewangan, jumlah mata
perlawanan bola sepak disepanjang musim
dan jumlah kos disepanjang
tempoh masa perakaunan. Lajur ke lima Jadual 2.3 menunjukkan kekerapan terkumpul bagi taburan kekerapan Jadual
2.2.
Contoh
2.1
Sebuah syarikat air mineral biasanya mengisi air di
dalam botol sebanyak 500 ml. Sampel rawak 50 botol air mineral
telah diambil dan disukat isi kandungannya adalah sebagaimana berikut:

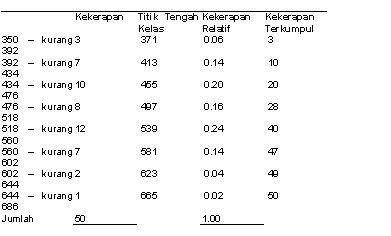
Binakan taburan kekerapan bagi data ini menggunakan lapan kelas.
Kirakan titik tengah kelas, taburan kekerapan, dan
kekerapan terkumpul bagi taburan kekerapan ini.
Penyelesaian:

Langkah
3: Tentukan luas
jeda kelas.
Titik akhir kelas pertama mestilah 360 atau kurang supaya
nilai terkecil dapat dimasukkan di dalam kelas pertama, dan titik akhir kelas
terakhir mestilah 690 supaya nilai terbesar dapat dimasukkan kedalam kelas
tersebut. Taburan kekerapan, titik tengah kelas, kekerapan
relatif dan kekerapan terkumpul adalah sebagaimana jadual berikut.
Geraf
dan Carta
Salah satu daripada mekanisma yang paling berkesan di dalam
mempersembahkan data di dalam
bentuk yang bermakna untuk pembuat keputusan ialah di dalam bentuk geraf. Melalui geraf dan
carta, pembuat keputusan biasanya memperolehi gambaran keseluruhan bagi data
dan mencapai beberapa rumusan yang amat berguna dengan hanya mengkaji carta atau geraf. Menukarkan data kepada
geraf merupakan aktiviti yang kreatif dan berseni. Salah satu daripada
penggunaan penting geraf di dalam statistik adalah untuk membantu penyelidik
menentukan bentuk taburan.
Lima bentuk geraf yang akan dibincangkan
disini: (1) histogram, (2) poligon kekerapan, (3) orgif (4) carta pai dan (4)
lakaran batang dan daun.
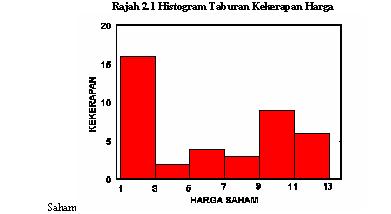
Histogram
Histogram ialah
jenis carta bar menegak untuk menerangkan taburan kekerapan. Pembinaannya
melibatkan kita melabelkan paksi-X sebagai titik akhir kelas dan paksi Y adalah
sebagai kekerapan. Rajah 2.1 menunjukkan histogram bagi taburan kekerapan untuk Jadual
2.2. Histogram
merupakan alat yang berguna untuk membezakan di antara selang kelas. Dengan melihat secara imbas
kepada histogram dapat menunjukkan kepada kita selang kelas yang memberikan
jumlah kekerapan yang tertinggi. Rajah 2.1 dengan nyata
menunjukkan jeda kelas 1-di bawah 3 mempunyai kekerapan yang tertinggi (16).
Histogram boleh menunjukkan
kepada kita dimana peningkatan atau penurunan yang besar terjadi di antara kelas, seperti dari kelas 1-di bawah 3
kepada 3-di bawah 5, penurunan 14, dan daripada kelas 7-di bawah 9 kepada kelas
9-di bawah 11, peningkatan 6.
Poligon
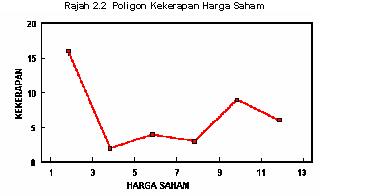
Kekerapan
Poligon kekerapan merupakan geraf dimana segmen garisan ‘menghubungi
titik tengah’ di antara taburan
kekerapan. Pembinaan poligon kekerapan
bermula, dengan menskalakan
titik akhir kelas disepanjang paksi-X dan nilai kekerapan disepanjang paksi-Y. Titik adalah dilakarkan
bagi nilai kekerapan pada titik engah
setiap selang kelas. Menghubungi
titik tengah ini akan melengkapkan poligon. Rajah 2.2 merupakan poligon
kekerapan taburan data dari Jadual 2.3.
Maklumat yang
diperolehi dari poligon kekerapan dan histogram adalah sama.
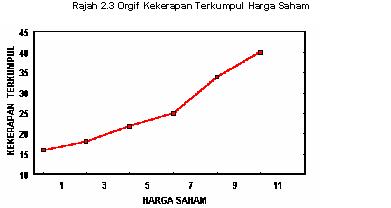
Ogif
Orgif adalah poligon kekerapan terkumpul. Pembinaan orgif bermula dengan melabelkan
paksi-X dengan
titik akhir kelas dan paksi-Y dengan kekerapan terkumpul. Rajah 2.3 menunjukkan orgif
bagi kekerapan terkumpul di dalam Jadual 2.3. Orgif
amat berguna apabila pembuat keputusan mahu melihat jumlah disepanjang tempoh
masa. Kecerunan yang curam bagi orgive boleh digunakan
untuk menunjukkan peningkatan yang
mendadak di dalam kekerapan. Di dalam Rajah 2.4 kecerunan yang curam berlaku di dalam kelas 1-di bawah 3 dan
kelas 9-di bawah 11.
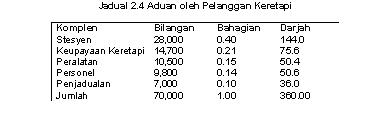
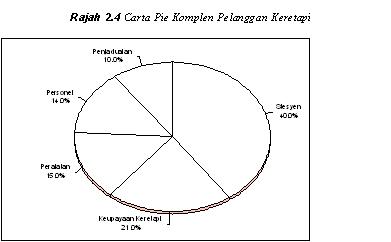
Carta Pie
Carta pie merupakan bahagian data dimana kawasan keseluruhan pie mewakili
100% daripada data yang dikaji dan
kepingan pie merupakan peratus pecahan sub-level. Ia digunakan dengan meluas di dalam perniagaan,
terutamanya untuk menggambarkan beberapa perkara seperti kategori belanjawan,
bahagian pasaran, dan pengagihan masa dan sumber. Jadual 2.4 menunjukan jumlah aduan yang
diterima oleh perkhidmatan kereta api dan Rajah 2.5
menunjukkan carta pie.
Batang dan Daun
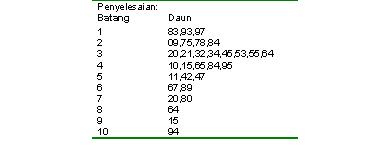
Cara lain untuk menyusun data mentah kedalam
kumpulan ialah melalui lakaran batang dan daun. Teknik ini
adalah mudah dan memberikan pandangan unik bagi data. Lakaran
batang dan daun merupakan pembinaan melalui pengasingan digit bagi setiap
nombor data kepada dua kumpulan, batang dan daun. Digit yang terkiri sekali
sebagai batang dan mengandungi nilai
digit yang tertinggi. Digit yang paling kanan sekali merupakan daun dan mengandungi nilai yang rendah. Jika set data mempunyai dua digit, batang
merupakan nilai disebelah kiri dan daun adalah nilai disebelah kanan. Sebagai contoh, jika 34 adalah satu nombor, batang adalah 3 dan daun
adalah 4. Bagi
nombor yang mempunyai lebih dari dua gigit, pembahagian batang dan daun adalah
bergantung kepada citarasa penyelidik.
Jadual 2.5 mengandungi skor
pemeriksaan polisi keselamatan kilang terhadap 35 orang pekerja.
Lakaran batang dan daun ditunjukkan di dalam Jadual
2.6. Kebaikan taburan ini
memberikan pembuat keputusan melihat sama ada skor
terletak dikedudukan teratas atau terbawah dan menentukan serakan skor
tersebut. Kebaikan kedua ialah nilai
data mentah yang asal
adalah dikekalkan.
Jadual 2.5 Skor Pemeriksaan
Keselamatan Kilang
|
86
|
77
|
91
|
60
|
55
|
|
76
|
92
|
47
|
88
|
67
|
|
23
|
59
|
72
|
75
|
83
|
|
77
|
68
|
82
|
97
|
89
|
|
81
|
75
|
74
|
39
|
67
|
|
79
|
83
|
70
|
78
|
91
|
|
68
|
49
|
56
|
94
|
81
|
Contoh 2.2
Berikut ialah data yang mewakili kos bagi sampel 30 harga saham harian di KLSE.
|
6.67
|
2.75
|
5.47
|
4.65
|
3.32
|
2.09
|
1.83
|
10.94
|
1.93
|
6.89
|
|
7.20
|
2.78
|
3.34
|
7.80
|
3.20
|
3.21
|
3.55
|
3.53
|
3.64
|
4.95
|
|
5.42
|
8.64
|
4.84
|
4.10
|
915
|
3.45
|
5.11
|
1.97
|
2.84
|
4.15
|
Menggunakan
ringgit sebagai batang dan sen sebagai daun, binakan lakaran batang dan daun
bagi data tersebut.

6.2.2
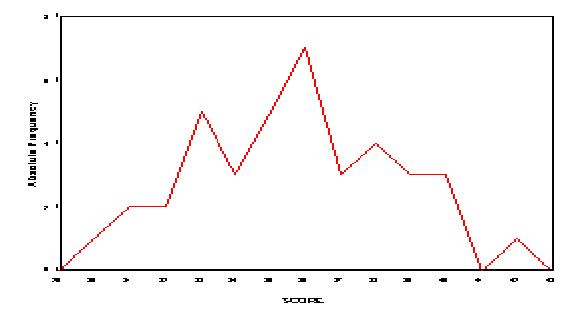
Analisis Taburan dan Grafik
Sampel taburan adalah hasilan sample
yang dipungut dari data asal. Ciri utama sample tersebut adalah bilangan skoran
yang boleh dikira, bilangan skoran yang diwakili dengan huruf N. Sebagai contoh, data berikut adalah dipungut :
|
32
|
35
|
42
|
33
|
36
|
38
|
37
|
33
|
38
|
36
|
35
|
34
|
37
|
40
|
38
|
36
|
35
|
31
|
37
|
36
|
33
|
|
36
|
39
|
40
|
33
|
30
|
35
|
37
|
39
|
32
|
39
|
37
|
35
|
36
|
39
|
33
|
31
|
40
|
37
|
34
|
34
|
37
|
Nombor-nombor ini
adalah nombor yang mewaikil taburan sample. Dari perwakili
nombor-nombor tersebut polygon kekerapan boleh dinyatakan.
Taburan sample yang dimaksudkan
boleh di istilahkan sebagai
statistics. Contoh-contoh statistic yang
dimaksudkan adalah min, median, mod, sisih piawai, julat dan lain-lain.
Jika sample yang lain dipersembahkan , pnskoran yang lain akan terbentuk. Poligon
kekerapan relative akan turut dipersembahkan secara
berlainan.
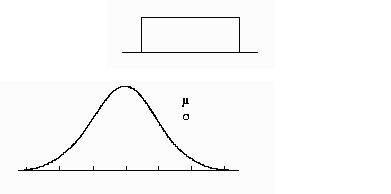
Bagi mengelak
kekeliruan model keberangkalian wujud secara teori dimana maklumat penuhnya
adalah ternyata.
Model kebarangkalian ini biasanya dinyatakan didalam bentuk graf
. Dua model geraf yang boleh disaksikan dinyatakan seperti taburan
uniform dan lengkuk normal.
6.2.3
Analisis Taburan Kumulatif dan Grafik
Langkah pertama
dalam membentuk polygon kekerapan relative aalah dengan membahagikan kumulatif
kekerapan obsolute dengan kekerapan bilangan skor. Kumulatif kekerapan relative menjadi :
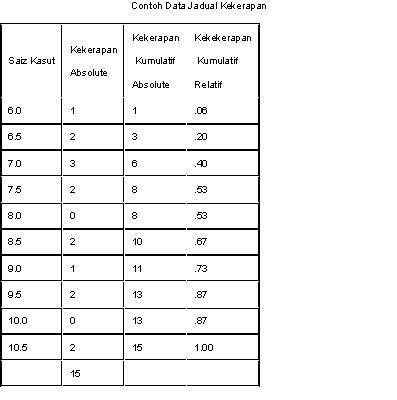
Dengan melukis paksi-X dan paksi-Y
bagi kekerapan kumulatif relative anda akan
memperolehi graf seperti dibawah.
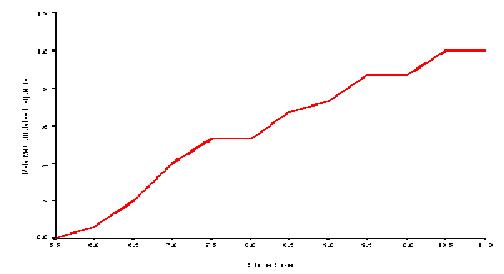
6.3
Kencenderungan Memusat dan Serakan
Taburan
memusat adalah sekumpulan taburan yang mempunyai bentuk yang sama
. Taburan skoran tertumpu dibahagian tengah daripada
kawasan ekor. Juga dikenali dengan
nama “bentukan loceng”. Ketinggian
taburan memusat boleh dispesifikasikan dalam dua parameter iaitu min (μ)
dan sisihan piawai (σ).
6.3.1
Ukuran Kecenderungan Memusat
Satu jenis pengukuran yang digunakan untuk memerihalkan set
data adalah ukuran kecenderungan memusat.
Pengukuran kecenderungan memusat menghasilkan maklumat
berkaitan dengan titik tengah pada satu kumpulan nombor. Sukatan kecenderungan
memusat adalah satu nilai pusat yang dapat mewakili keseluruhan nilai data.
Dengan mengetahui nilai pusat sesuautu data, kita akan
dpat mengambarkan yang lebih paik tentang cirri-ciri populasi yang di
maksudkan. Terdapat tiga jenis sukatan kecenderungan memusat
yang selalu digunakan iaitu min, mod dan median.
Di antara ukuran yang memerihalkan data secara mumerik ialah
sukatan kecenderungan memusat . Sukatan kecenderungan
memusat yang akan diperkenalkan di sini ialah min,
median, mod dan persentil ke-p. Andaikan set cerapan bagi pembolehubah rawak X
dari satu sampel
bersaiz n ialah {x1, x2, x3,
…….., xn}.
Maka
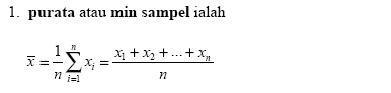
Purata atau min sampel adalah satu sukatan
kecenderungan memusat.
Sukatan kecenderungan memusat pada dasarnya adalah satu
titik yang mana cerapan yang lain gemar berlegar
hampir kepadanya. Ia juga boleh jadi titik yang
menandakan kedudukan pertengahan satu set data.Sukatan kecenderungan memusat
yang lain ialah
2. Mod, iaitu cerapan yang paling kerap timbul dalam
set data.
3. Median, yang cara
kasarnya, ialah nilai cerapan yang menjadi
penengah set data setelah semua cerapan
dalam set data tersebut
disusun secara menaik.
‘Penengah’ set data boleh ditakrifkan sebagai satu nilai di
mana 50%
cerapan bernilai kurang daripadanya dan 50%
lagi cerapan bernilai lebih
daripadanya.
Secara aritmetik median satu set data ditentukan mengikut
langkahlangkah
berikut:
1. Susunkan data cara menaik,
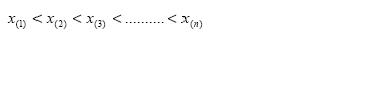
di mana (i ) x ialah
cerapan di kedudukan ke I setelah semua cerapan disusunkan.
2. Kirakan median, (m) x ,
seperti berikut:

Contoh 2.2.1 Tentukan min, median dan mod bagi sampel yang terdiri dari
cerapan berikut: 8, 5, 2, 5, 7, 5, 1.

Data yang disusun ialah 1, 2, 5, 5,
5, 7, 8. Maka median ialah 5.
Mod bagi set data ini ialah 5 juga kerana 5 timbul paling
kerap, iaitu 3 kali.
6.3.2
Ukuran Serakan dan Serakan Piawai
Ukuran
kecenderungan memusat menghasilkan maklumat berkaitan titik tertentu bagi set
data. Walau bagaimanapun, penyelidik
boleh menggunakan kumpulan alatan analisis lain untuk menerangkan set
data. Alat ini ialah ukuran serakan yang
menerangkan serakan atau pencaran set data.
Menggunakan ukuran serakan bersama-sama ukuran
kecenderungan memusat membuatkan pemerihalan numerik bagi data lebih lengkap
lagi.penghampiran sahaja.
variansnya
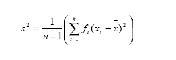
Contoh 2.3.1 Set data {2, 2, 1, 5, 1, 1, 4, 3} boleh juga dijadualkan
begini

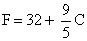
Dengan itu min set data di atas ialah
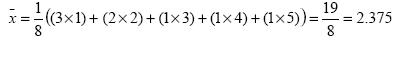
Untuk mengira varians lebih mudah jika semua nilai yang
diperlukan dipaparkan dalam jadual seperti berikut:


6.3.3 Skor Piawai
Skor piawia adalah skoran yang dibentuk. Skoran ujian mentah (bilangan skoran yang betul) di bentuk untuk
menunjukkan dimana skoran tersebut berada dengan min skoran yang diperolehi. Ini bagi membolehkan skoran
mentah dibandingkan dengan mana-mana ujian yang dijalankan. Ini juga membolehkan tafsiran skoran ujian jelas dilihat.
Seseorang boleh menentukan di mana skoran tersebut berada berbanding dengan
kebolehan keseluruhan atau dengan individu yang lain
atau dengan skoran kumpulan. Kaedah ini penting apabila kita
menjalankan piawai keatas populasi yang besar.
- Kebanyakan
skor piawai ujian yang dijalankan oleh ahli akademik dan ahli psikologi
mengunakan skor piawai yang diperolehi dari skor z ( z
scores. )
- Kebanyakan
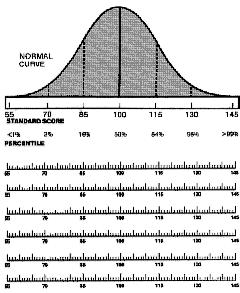
ujian menggunakan skor piawai dengan min 100 dan sisihan piawai 15.
- Skor
piawai 100 adalah pada min atau persentil 50%. Skor piawai 85 adalah satu
sisihan paiwai dibawah min dan skor piawai 115 adalah satu sisihan piawai
diatas min
- 68%
dari populasi berada di atas satu
sisihan piawai min dan satu sisihan piawai dibawah min. Ini adalah
julat purata yang dikenali sebagai julat skor dari -1 hingga + 1.
- Oleh
kerana skor piawai adalah konsisten sepanjang ujian ,
skor bagi seseorang itu boleh dibandingkan dengan ujian yang dijalankan.
Sesorang yang mempunyai IQ atau kecerdasan 110 dijangka mempunyai skor
pencapaian membaca disekitaran yang sama. Jika tahap
pencapaian membaca beliau adalah 90, iaitu 20 skor dibawah tahap maka skor beliau adalah
110-90= 20 skor. Perbezaan ini adalah satu sisihan piawai dan perbezaan
ini adalah perbezaan signifikan.
- Kebanyakan
skor ujian pencapaian mempunyai min 10 dan sisihan piawai 3
Contoh mudah bagi skor piawai ialah skor z ( z-score)
. Skor ini menunjukkan sisihan skor dari min atau
skor purata
atau sekumpulan skor yang berkaitan dengan sisihan piawai. This score is an indication of
the deviation
of a score from the mean, or average score, or a group of scores in relation to
the standard
deviation. Berikut adalah satu senarai skor
mentah yang diperolehi didalam sesuatu ujian.
Johan 78 Baharom 67
Mariam 92 Paul 91
Maria 62
Danish 94
Farid
98 Romzi 51
Rashid 72
Bariah 81
Pang 61
Leong 85
Daud 88
Suzi 42
Rentung 78
Haris 78
Teng 80 Johari 78
Mas 68
Tengku 82
Katakanlah gred sekolah tersebut pada lekukan loceng (bell curve) adalah A,B,
C,D,F. Bagaimnakah kita hendak memberikan gred pada kelas tersebut ?
Gred tersebut hendaklah atau mesti dibentuk.
- Rumus
yang boleh kita gunakan bagi mengira skor z adalah :
Skor piawai (z score)= skor mentah (gred ujian)(X)-min(M)
sisihan piawai(S.D.)
Oleh itu
1. Cari nilai min kelas. Nilai min adalah jumlah
keseluruhan skor mentah dibahagikan dengan bilangan pelajar yang mengambil
ujian. Min kelas adalah 76.3
2. Cari nilai sisihan piawai
Anda akan memperolehi min ujian adalah 76.3 dan sisihan
piawai 14.07. Untuk menentukan gred ujian akan
menurun atau tidak kita boleh mengunakan skor z. Skor ini akan dianggap
mempunyai min 100 dan sisihan piawai 14. Skor z bagi
setiap individu diperolehi dengan mengambil skor individu dan ditolak dengan
min dan kemudiannya dibahagikan dengan sisihan piawai.
Oleh itu jika skor Johan diambilkira
maka skor z bagi beliau adalah
=> 78-76.3/14.07=.12. Skor Johan adalah hampir dengan min
Jika kita lihat skor Suzi, skor z
beliau adalah berlainan iaitu
42-76.3= 34.3/14.07= -2.43. Menunjukkan skor
Suzi adalah 2 sisihan piawai dibawah min.
Dengan mengunakan
kaedah ini, kita boleh membuat perbandingan pencapaian relatif skoran bagi
setiap sesi latihan ujian.
Rumusan
Membuat analisis, interpretasi, dan kesimpulan
merupakan peringkat yang paling penting dalam proses penilaian. Hal ini
demikian kerana dapatan daripada kesimpulan ini akan menjadi pertimbangan asas
untuk membuat cadangan dan tindakan yang selanjutnya untuk memperbaiki ujian
dan amalan yang kurang memuaskan atau menjadi asas untuk mengubahsuaikan proses
pengujian seterusnya.
Rujukan :
Buana; Pengajar Jurusan
Sejarah Universitas Negeri Makassar . Ujian Nasional: Penilaian atau Evaluasi?
Garfield. Joan. (1992) Assessment and Teaching Statistics
, JSE
Sarle. Warren S.
(1997) Disseminations of the International Statistical Applications
Institute, volume 1, edition 4, 1995, Wichita: ACG Press, pp.
61-66.
http://home.gwu.edu/~kkid/sscore.htm