Planes of Empty Space

So far, the 'planes' within the arrays we have been dealing with have been more or less assumed to be 'solid' - (like a brick is solid) - as opposed to being 'empty space'. Not that there's anything about dealing with solid structures - (i.e., a toothpick, an index card) - that interferes with the material: but in order to proceed forth into the next section, it is necessary to switch to planes of empty space. And what is the reason?

When we use the terms 1-space, 2-space, 3-space, (areas within which lines can come together at right angles), we are referring to areas within which objects can freely rotate, move, and travel. But just as no Linelander can "exist within" a solid segment, no Flatlander can "exist within" a solid square. (And no one of the 3rd dimension need be told that he cannot "exist within" a giant solid concrete block!) From now onward the 'planes' that we will be working with, we will consider to be hollow.

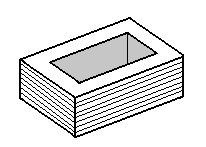
For example: 'solid' index cards (as they are normally), when 'stacked' upon a tabletop, form more or less a solid cube - which in essence could be considered by fundamental nature the equivalent of a brick. Clearly, a 'brick' is not a good, or even a successful, model of 3-space (a 'cubic volume' of empty space) as we know it to be. Instead, let us assume that the index cards 'stacked' upon the tabletop are hollow (that is, the inner area of each card is 'cut out' and removed - the only 'solid' part remaining is a thin border that more or less "contains" the empty space - in the same way the frame of a picture 'contains' the picture). The result of stacking the index cards this time is a hollow cube possessing 4 of its 6 sides, as is portrayed in the diagram on the left. The 2 sides that are missing, if they existed, would make up what we would call the 'top' and 'bottom' of the hollow cube. And what we find to exist within the hollow cube is none other than a cubic volume of empty space (that is to say, 3-space)! (Take note that the task of 'stacking' hollow index cards upon the tabletop was in no way different than the task of 'stacking' the solid ones (though the finished products are indeed different). This 'property' can be said to hold true for solid and hollow planes of any dimension in which planes will need to be stacked.)

On the topic of stacking, recall the diagram presented earlier in the material: after the 3rd-dimensional structure (the 'brick') finishes being constructed, there is somewhat of a 'dead end' that is reached. It's not that the concept of an array of 'bricks' (solid cubes) is a problem - but rather, the direction into which the cubes would extend when stacked - 'how does one extend a line in a direction perpendicular to a cube'? This is indeed a complex question. However, it is by relating lower-dimensional arrangements to our dimension in the same way that they relate to their own dimension - the reasoning system of analogy - that this question can be answered.

First of all, let us approach the solid cube (or 'brick') in the same way that the 'solid index card' (in a sense a 2-dimensional plane) in the diagram above was approached: though it may not at the moment be clear as to the 'direction' in which the solid cubes would extend into when stacked, what we can do, at least for now, is make clear the structure of the '3-dimensional planes' of empty space that we will be using. As of now, a 3-plane (3-dimensional plane) will be defined as a hollow cube. A hollow cube is the logical next step up from the hollow square / hollow index card we observed a 2-plane (2-dimensional plane) to be. The 3-plane that the hollow cube represents, then, is a plane of empty space, within which objects can freely 'rotate, move, and travel'.

Defining a 3-plane as a 'hollow cube' will allow us to implement a 'mental tool' that appears to have so much potential as a 'tool', it could be said to rival analogy itself in terms of usefulness! To begin with, you are probably sitting in a 'room' of some sort as you read this. Take note, that your 'room' happens to be very similar in structure to a hollow cube. So in essence, your 'room' could actually be referred to as a hollow cube about 10 feet long, wide, and high. Being aware of this will allow you to physically "participate" step-by-step along with upcoming sections - and will make the material in them, as you will see, not only easier to understand, but more 'meaningful' as well.

On the topic of 'rooms', let us observe the Linelander and Flatlander in their own rooms. The 'room' that a Linelander (a being whose life is limited entirely to length) is familiar with is a hollow segment, which the Linelander can think of as being a 1-dimensional plane. Equally so, the 'room' a Flatlander (a being whose life is limited entirely to length and width) is familiar with is a hollow square, which the Flatlander can think of as being a 2-dimensional plane. Pictures of each subject in his "room" are displayed on the right.

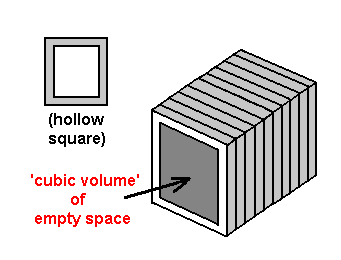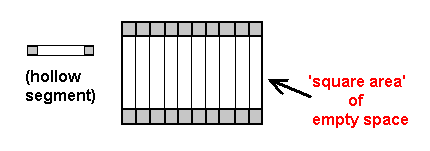
It was observed earlier - in the stacking of a pile of 'hollow index cards' - how the individual 'empty space' within 'lined up' planes of empty space can all "combine" to form a single, higher space (in the case of the 'hollow index cards', 3-space). When we 'line up' empty 1-planes / 'hollow segments' / Linelander rooms, as is done above on the left, we get similar results: the combined 'empty space' of individual, multiple 1-planes forms what we know as 2-space (or rather, a 'square area' of empty space). 'Lining up' empty 2-planes / 'hollow squares' / Flatlander rooms (as is done below on the left), furthermore, as you may have already found out, produces a structure equivalent to the stack of 'hollow index cards' - forming a '3-dimensional volume' of empty space.

If we were to 4-dimensionally 'line up' empty 3-planes / 'hollow cubes', into what direction would they extend? If we were indeed able to construct such an 'array of 3-planes', analogy would quite clearly suggest that we could simulate 4-space by "combining" the individual 'empty spaces' of each separate 3-plane into a single, higher 'empty space' - a "hypercubic hypervolume" of empty space. How, though, would one go about constructing such an array? A first step would be to consider your room - itself a 'hollow cube' - to be a 3-plane in the middle of an array of 3-planes. What better place to study a 3-plane array than from within it?