Studying the Hypercube

Just as a square could be considered to be an array of segments, and a cube, an array of squares, a hypercube could be considered to be an array of cubes. We are all familiar with the corner of a square - in which 2 edges meet each other at right angles, and with the corner of a cube - in which 3 edges meet each other at right angles. The corner of a hypercube involves 4 edges meeting each other at right angles. This is a feat that no 3-dimensional structure can perform. A hypercube, however, is a 4-dimensional structure (in that it exists simultaneously across multiple 3-planes) - and can handle the task. To clarify how we experience a hypercube, we will first take note of a Flatlander's experience of a cube, and apply what we learn to the hypercube.

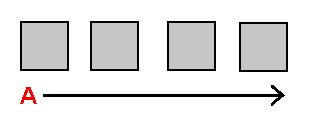
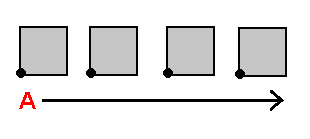
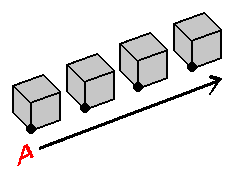
A Flatlander cannot experience a cube "all at once", but can only experience one slice of it at any given time. The highlighted square in the diagram on the left represents the slice of the cube that lies on the Flatlander's plane. The stack-diagram displays how a Flatlander would conceive of the cube, and the illustration to its right represents the 'stacked cube' as it exists in physical reality. Due to the limitations of the dimension to which the 2-plane of the Flatlander is confined, no means exists of designating the spatial separateness of the squares on 2-planes above his own 2-plane, from the 2-plane he inhabits - it's as if all of the slices A-ward from the Flatlander's plane occupied the "same space" as the slice on his own plane. That is, because the Flatlander lacks knowledge of a third spatial coordinate, he has no way of 'expressing' how the slices of the cube are spatially 'separate'. This is not a problem, however, because the Flatlander can refer to the stack-diagram of the stacked cube to envision the spatial separateness of the square on each 2-plane.

Assume that the highlighted cube in the stack-diagram on the right represents the hypercube slice - of the slices of a hypercube - that lies in your room (a 3-plane in the middle of an array of 3-planes). If we in fact experience the slices of a hypercube in the same way that a Flatlander experiences the slices of a cube, we would be able to experience only one slice of the hypercube at any given time (the slice that lies on our 3-plane). Because our dimension cannot 'express' how the hypercube slices on the 3-planes A-ward are spatially separate from our own 3-plane, we can at best say that the slices lying on the 3-planes A-ward occupy the "same space" as the slice on our own 3-plane. What a stack-diagram, however, allows us to do, is to view the slices as being spatially separate, and to assign a fourth spatial coordinate to each slice.

So that we can better understand the properties of a 'stacked hypercube', we will first examine the properties of a stacked cube. Upon examining the top stack-diagram on the left, imagine that each slice has a unique 3-dimensional depth from you. Next, without altering your flat view of the slices, imagine moving the slices behind and in front of each other so that in assuming their unique 3-dimensional depths they form a cube. The slices are 3-dimensionally aligned in the sense that matching corners on all of the slices are lined up. You are now viewing the 'top slice' of the '3-dimensionally aligned' cube, and "behind" this slice - hidden from our view - lies the remaining slices. As of your field of vision, the squares appear to cover the same visual area. That is, no 2-dimensional means exists of expressing the separateness of the visible 'top slice' of the cube from the slices concealed behind it. Because a Flatlander lacks knowledge of a third spatial coordinate, he cannot grasp the '3-dimensional depth' separating the slices that is so evident to us. Lacking knowledge of the concept of '3-dimensional depth', the Flatlander could at best assume the slices of the cube to all occupy the "same space".

Take note that the same concepts would hold true for the 4-dimensional 'alignment' of the slices of a hypercube (presented in the bottom stack-diagram to the left). As with the slices of the cube, slices of a hypercube that are 4-dimensionally aligned are slices for whom matching corners are lined up. In order for this to occur, however, all of the slices must share the "same space". This is a feat we are not unfamiliar with. Imagine a 3-plane array much like the one described in previous sections. You are then to assign a cube to your room (the central plane of the 3-plane array), and then "stack-glide" the cube into the 3-planes lying A-ward. The 'gliding' of a cube, take note, is a 4-dimensional process. When a cube is 'glided', it moves in a direction that no 3-dimensional means of reasoning can portray - a direction that brings the cube to a position that can at best be said to occupy the "same space" as when it started out. If desired, imagine each "stack-glide" of the cube forward (in its 4-dimensional direction of traversal) to itself leave behind a cube perceived as measurably smaller than the cube "stack-glided" before it - smaller for the same reason that the inner cube of a tesseract is smaller than the outer cube of a tesseract. After a cube is "stack-glided", the resulting slices of the hypercube can be considered separate only by means of a way not expressable, as stated, as of the limitations of our own dimension. However, it is by means of the medium of the stack-diagram that we can designate the spatial separateness of the slices of the hypercube, assigning each slice its own specific fourth spatial coordinate. Now that we are familiar with the fundamental concepts behind the cube and the hypercube, we will now focus on a more defined area of the structures: their corners.

The top stack-diagram on the left displays the slices of a cube, with a given corner of each slice 'marked'. This 'mark' on each slice represents a cross-section of a line. To make sense of these 'cross-sections', imagine 'aligning' the corners of the slices in the same manner described above: assign a unique 3-dimensional depth to each slice, and move the slices behind and in front of each other - without altering your flat view of the slices. Once the slices are in position, it becomes quite clear how the cross-sections combine to form a line. By assigning a third spatial coordinate to the 'mark' on the corner of each slice of the cube, we can easily visualize the spatial separateness of each mark, and understand the role that 3-dimensional depth has in the line's formation. This stack-diagram represents a Flatlander's conception of the corner of a cube. As stated, the corner of a cube consists of 3 edges meeting at right angles - a feat that cannot be performed in the 2-dimensional world of the Flatlander.

The next stack-diagram on the left is a stack-diagram displaying the slices of a hypercube, each 'marked' in the same fashion as the slices of the cube. Each 'mark' represents a cross-section of a line. What if we were to 4-dimensionally 'align' the slices so that matching corners are lined up? To visualize this, first begin with a cube in your room (a 3-plane in the center of an array of 3-planes) and "stack-glide" it A-ward. Though the slices of the hypercube occupy the "same space" 3-dimensionally, 4-dimensionally the slices are separate. The 'marks' on the matching corners of the slices of the hypercube represent a line extended perpendicular to the hypercube slices themselves. 4-dimensionally 'aligning' matching corners on the slices of the hypercube, then, forms the fourth edge of the 4 perpendicular edges found coming together at the corner of a hypercube. Given that a hypercube is an array of cubes, the common corner shared by the cubes forming the hypercube would form a line. In understanding how the cross-sections on the corners of the hypercube slices form a line, we are to recall the emphasis of the "3-dimensional depth" described in the material above concerning the 'marked' slices of a cube. If we were to apply a "4-dimensional depth" to the cross-sections of the cubical corners of a hypercube, it would be by means of an unknown, but very real direction that the cross-sections on the corners of the hypercube would extend forth to form a line. The line, in turn, would extend outward in ways not describable by any 3-dimensional means of reasoning. Let this inform us as to the properties and structure of the hypercube.