Outside a 3-dimensional Surface

You may recall from a past section the proposal that in a certain future section we would go beyond our standard means of visualizing an array of 3-dimensional planes, and assume a viewpoint that existed from a 4-dimensional point of view. We have now arrived at that section. Up until now, our best conception of the 4-dimensional occurrence known as an array of 3-dimensional planes existed in the form of a "compressed" array of 3-dimensional planes. For someone to "compress" an array of planes, by definition, means for him to imagine the planes making up the array he occupies to all assume the space that he perceives his own plane to take up. A "compressed" array of 3-dimensional planes, as you may recall, is not a physical structure, but is rather a mental concept invented for our use as a way to envision what we understood to be planes that extended perpendicular to our dimension. The main purpose of this section, take note, is to review what it means to think in terms of a "compressed" array of planes, which we've just done, and to then offer an alternate means of conceiving of an array of 3-dimensional planes. In doing so we will have before us 2 methods of visualization, each representing a unique purpose.

What would those purposes be? The purpose that the concept of a "compressed" array of 3-dimensional planes has fulfilled, as we've witnessed, is the construction of 4-dimensional objects. In addition to allowing us to successfully portray structures such as the hypersphere, the arrangement of planes that a "compressed" array of planes provides can give one substantial insight as to how the concept of multiple instances of one's own plane relates to the next dimension. Though thinking in terms of "compressed" planes is a medium that provides the multiple planes that succeed in serving the purposes just mentioned, there is a limitation as to what "compressed" planes can accomplish: thinking in terms of "compressed" planes offers no means of visualizing the higher-dimensional directions that the very planes it provides extend into.

You see, the introduction of each new dimension provides a new pair of directions into which extension can occur. As was demonstrated in the "compressed" plane sequence, it is into these 2 opposite directions that the planes of the previous dimension extend, forming a distinct linear array. In summary: we can conceive of the concept of multiple 3-dimensional planes. We have not yet, however, successfully conceived of the 4-dimensional directions that these 3-dimensional planes would extend into, given that they are in fact arranged in a linear fashion. Why not? We have not attempted to perform such a feat yet because the whole "compressed" plane technique (which has been our method of study) is centered around what our senses experience concerning the space we perceive our plane to take up. In order to conceive of the 4-dimensional directions spoken of above, we must leave behind our conception of the internal workings of the plane we are confined to, and go outside of the plane in a way that we never have before.

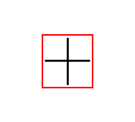
To better understand the nature of this topic, we must first fully understand what it means to exist within a surface. As we all know, from within a 2-dimensional surface there are at most 2 lines that can cross each other and at the same time lie at right angles to each other. Assume that on the surface of a sphere lies 2 such crossed lines. Next to the crossed lines is a Flatlander trying to visualize the extension of a third line perpendicular to the original 2 lines. Will the Flatlander succeed? Probably not. Why not? Visualizing extension perpendicular to a surface, from within that surface, is impossible, because the very directions of extension that are perpendicular to the surface, extend outside of the surface itself. No direction that the Flatlander comes up with will ever leave that surface! Hence, in order to extend perpendicular to an object within a surface (such as the crossed lines), you must leave that surface.

The Flatlander, you see, in asking how to extend perpendicular to an object within his surface (the crossed lines) asks the wrong question. The question to ask, rather, is that of how to extend perpendicular to the surface itself. To attempt to answer such a question, however, is to perform a feat that goes far beyond the knowledge that mere sensory experience can provide. In order to fully understand this, one must first consider the notion that it is impossible to relate to the external configuration of a surface that you yourself exist within! Perhaps what could be the classic example of this concept goes along the lines of someone on the surface of a sphere (such as the earth) having no way of detecting that he is in fact on a sphere. It is knowledge of the 'external configuration' of a surface, however, that allows us to go outside of the surface and hence visualize extension perpendicular to it. Already having obtained knowledge of the 'external configuration' of the surface of a hypersphere from previous sections, we will have no difficulty in participating in upcoming material that includes involvement with the surface of the hypersphere.

How would the Flatlander in the example above visualize a third line perpendicular to the two he's familiar with? Presented to the right is a flat view of the 2 crossed perpendicular lines mentioned above. We know that the limitations of the 2-dimensional surface the lines are confined to make a third perpendicular line impossible. To a Flatlander, a third perpendicular line is impossible because his visualization skills do not go beyond the 2-dimensional surface he is confined to. To visualize a third perpendicular line the Flatlander must relate to the 2 crossed lines from outside the surface he is limited to. This will be done by placing the crossed lines on the surface of a sphere. This is done to the right, in stack-diagram form, in the form of cross-sections spread across the slices of the sphere. As you can see, one of the lines exists entirely on the central slice. The points on the surrounding slices represent both ends of the line perpendicular to the line on the central slice. To picture the crossed lines as they would appear on the actual sphere, move the slices on both sides of the central slice over to their actual 3-dimensional positions behind and in front of the central slice. In the next stack-diagram to the right we add the 'third line' to the 2 crossed lines already on the surface of the sphere (in the form of points representing the ends of the line). This stack-diagram represents a Flatlander's basic conception of extension perpendicular to a 2-dimensional surface.

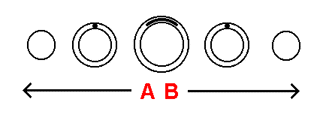
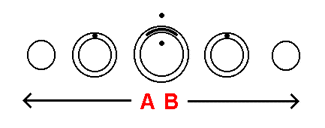
How would we visualize a fourth line perpendicular to the three we're familiar with? Presented to the left are the 3 crossed lines we are familiar with, as they appear from within the 3-dimensional surface that they are being viewed from. We know that the limitations of a 3-dimensional surface make a fourth perpendicular line impossible. To visualize a fourth perpendicular line we must relate to the 3 crossed lines from outside the surface we are limited to. We will do this by placing the crossed lines on the surface of a hypersphere. This is done to the left, in stack-diagram form, in the form of cross-sections spread across the slices of the hypersphere. As you can see, 2 of the crossed lines exist entirely on the central slice. The points on the surrounding slices represent both ends of the line perpendicular to the lines on the central slice. In the next stack-diagram to the left we add the 'fourth line' to the 3 crossed lines already on the surface of the hypersphere (in the form of points representing the ends of the line). This stack-diagram represents our basic conception of extension perpendicular to a 3-dimensional surface.

Imagine that the 3 crossed lines spread across the surface of the hypersphere above represent the 3 dimensions of what is a 3-dimensional room on the surface of a hypersphere. The stack-diagram below on the right makes this room known in the form of 2-dimensional cross-sections spread across the surface of the hypersphere shown. Let us assume, then, that there is a 3-dimensional individual in this room occupied with the 3 crossed lines we are familiar with, trying to visualize the directions that 3-dimensional planes surrounding his own would extend into, given that his room was the central plane of the array. This person's experience of this room is of a perfectly normal 3-dimensional room, much like the room you may be occupying right now. The room is within the surface of the hypersphere. Our view of the room is from outside the surface of the hypersphere.

Recall, if you will, the 'fourth line' perpendicular to the 3 crossed lines we are familiar with, as it appears in the previous stack-diagram. The directions that this line represents are in fact the directions that the person in the room on the surface of the hypersphere is trying to visualize. To better understand this person's situation, recall once again, if you will, from earlier in this section, the notion that states that visualizing extension perpendicular to a surface, from within that surface, is impossible, because the very directions of extension that are perpendicular to the surface, extend outside the surface itself. No direction that the person comes up with will ever leave the surface of the hypersphere! One can easily conclude, then, that it is impossible for the person to relate to the external configuration of a surface that he himself exists within! Take note, if you will, that the directions represented by what is the 'fourth line' in the previous stack-diagram are the very directions perpendicular to the room on the surface of the hypersphere, that the person in the room is trying to visualize. These directions are in fact the 4-dimensional directions spoken of in a previous section (as well as earlier in this section) - the directions into which the planes surrounding a central plane in an array of 3-dimensional planes would extend. From the point of view of the person within the surface of the hypersphere, these directions are what we've referred to in previous stack-diagrams as direction 'A' and direction 'B' - directions that before now we could not physically envision because we were limited to thinking in terms of "compressed" planes - a means of reasoning not specialized in the visualization of higher-dimensional directions.

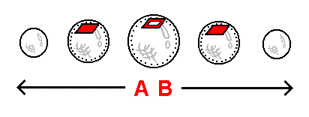It is this 4-dimensional viewpoint that allows us to clearly perceive directions that are in essence nonexistent to the person in the room on the surface of the hypersphere. As stated above, the 3-dimensional room in the stack-diagram to the right is spread across the slices of the hypersphere in the form of 2-dimensional cross-sections. A 3-dimensional room, it would happen, is by its own fundamental structure the equivalent of what we would define a '3-dimensional plane' to be. Assume, then, that the cross-sections of the 3-dimensional room represent what are the cross-sections of a 3-dimensional plane. Given that the inner slices of the hypersphere are hollow, and given that the surface of the hypersphere possesses a documentable "thickness", we will now attempt to "stack" layers of 3-dimensional planes above and below the level of the surface of the hypersphere - in essence forming the array that the person in the room is trying to envision. Because each layer (that makes up what we consider to be a 3-dimensional plane) possesses a specific amount of what we will call its own distinct 4-dimensional thickness, each layer of 3-dimensional planes accumulates upon previous layers and takes on a measurable 'separateness' from every other 3-dimensional plane in the array.

The portrayal of the 4-dimensional thickness of the 3-dimensional room in the stack-diagram above on the right was produced with the intention of successfully displaying the 3-dimensional room using as little cross-sections as possible. The resulting layout, being as simple as it can be, prevents any confusion that might occur due to unnecessary complication. As you can see, the cross-sections of the 3-dimensional room are square. The outer cross-sections (the floor and roof of the room) are solid. The inner cross-section (the walls of the room) is hollow. In this sense a 3-dimensional room can be thought of as being a hollow cube. As you may recall, the slices of the hypersphere as we have worked with them are also hollow. What if the solid and hollow cross-sections portrayed in the stack-diagram, rather than being square and representing a 3-dimensional room (which is a hollow cube), were circular and represented the central slice of a hypersphere (a hollow sphere)? We would be able to "4-dimensionally stack" the remaining smaller outer slices of the hypersphere above and below the central slice in the same way we imagined the cross-sections of the 3-dimensional room to be 4-dimensionally stacked. This allows us to directly visualize the sequential, linear separateness of each slice - something that cannot be acheived when thinking in terms of "compressed" planes.

Upon having covered the material presented in this section, we can claim to have gained a thorough understanding of the 2 alternate means (spoken of earlier in this section) of conceiving of an array of 3-dimensional planes. As stated, each of these 2 methods of visualization specializes in addressing its own unique set of purposes: thinking in terms of "compressed" arrays of planes is a medium that provides the multiple planes required to construct objects associated with the fourth dimension. The approach described in this section, in turn, allows us to document the properties of higher-dimensional directions of extension. In the next section we see how everything we've learned so far relates to how gravity works.