The Hypersphere and Time

In the previous section we saw how mass and motion worked together to produce the effect we call gravity. Mass makes gravity possible by curving the shape of the space surrounding the body we associate the gravity with. Motion, in the form of the expansion of the universe, provides the means by which curved space acts upon the objects that are falling. Mass and motion also happen to be the key factors involved in terms of how time operates. This would suggest that gravity and time are related at a deeper level: in the theory of relativity we find that conditions that cause changes in gravity cause changes in time as well, as is the case with a black hole. How do mass and motion relate to the concept we call time?

Our universe, the surface of an expanding hypersphere, is in a state of constant motion. We experience this motion as the passage of time. Throughout all regions of the expanding hyperspherical surface we find celestial bodies of all sizes and masses - from planets to stars to black holes. As stated in the previous section, it is the mass of each and every body that causes the body to 'sink down' into the hyperspherical surface, surrounding the body with a 'curved sag' that brings it down to a level below the level of the rest of the surface. Having been brought down to this level, the bodies are carried along with the surface of the universe as it expands, following from behind at a distance determined by how massive the body is: the more massive the body, the farther behind the rest of the expanding surface the body will be found to follow. Though this distance may vary based upon the mass of the body, the rate at which the bodies are carried along behind the expanding surface of the universe is the same for every body: it is a rate that can be observed to be equal to the rate of motion of the expanding hyperspherical surface itself. The reasoning behind this proposal is based upon the simple understanding that when the universe expands, it expands as a single united entity. It is because the universe expands as a 'single united entity' that all points on its hyperspherical surface can be found to engage in motion along with that surface in unison. Because there is but one expanding surface - a single surface that evenly distributes the effects of expansion throughout all points found to lie within it - expansion-related effects observed to be true within any given region of the expanding surface will always be equivalent to the expansion-related effects observed to be true within any other region of the expanding surface.

Given this reasoning, the rate of expansion of the hyperspherical surface of the universe can be considered to be the universal standard in terms of how the flow of time operates - the ultimate source that everything related to time would depend upon to function. What is meant by the term 'universal standard'? Given that the rate of expansion of the universe is a 'universal standard', you may reason, it must therefore also be an unchanging, constant rate of travel. Should the rate of expansion of the universe, then, be considered to be of a constant value? Let us attempt to understand the nature of what being a 'universal standard' means. Our best means of understanding the rate at which the universe is expanding, it would appear, lies in our ability to measure that rate of expansion. What would this process involve? To better understand the nature of this situation, consider the notion that the process we call measurement happens to be based fully upon the element we call comparison: the results of a measurement we make upon any given occurrence will always be found to be dependent upon a comparison performed upon an external, second occurrence. Any and all measurement applied to the occurrence being measured is based entirely upon the information obtained from this second occurrence. Without the information provided by the second occurrence, what is being measured has nothing to which it can compare itself, and hence the process we call measurement cannot take place.

Given the reasoning just presented, we can conclude that in order for something to be measured, there must exist a standard outside of what is being measured to which what is being measured can be compared. Measurement, by its very own nature, then, requires a standard of measurement external and separate from what is being measured, upon which a comparison is performed. We are quite familiar with the process we call measurement: everything that lies within the boundaries of our universe is measurable. This is true because from within the boundaries of the universe, there will always be some external reference available to which what is being measured can be compared. We have developed a vast collection of such units, that allow us to refer to the universe in terms of units that can tell us anything from how old the universe is to the distance across the universe. Take note, however, that if all measurements performed within the universe are ultimately references to a second, external standard, then we will never come across a unit of measurement that isn't dependent upon another supposedly pre-existing unit. Because all units of measurement are ultimately dependent upon another unit to be the units of measurement that they are, then, how will we ever know for sure whether the units we are using are in fact what we believe them to be?

This explains to us in detail the nature of what being a universal standard means: you cannot measure what you are not outside of. Universal standards exist in the form of the properties of the universe that they are associated with. If we were to attempt to measure a universal standard, our measurement would fail to work, because the measurable units through which we attempt to measure a universal standard, are themselves dependent upon the universal standard we are trying to measure, to be the measurable units that they are! Because the process of measurement requires of us to be external to what we are measuring, our attempt to measure a universal standard would be like comparing the universe to itself. Having been made familiar with the concept of a 'universal standard', we will address a question posed earlier: should a 'universal standard' such as the rate of expansion of the universe be considered to be constant in value? Does the rate at which the universe expands ever change? Because it is impossible to measure a property of the universe, detecting a change in that property is equally impossible. What this means is that if a change in a property of the universe occurred, we would not be able to detect that change: because all measurable occurrences within the universe related to that property of the universe are dependent upon that property to be the measurable occurrences that they are, when the property changes, the occurrences, put simply, change along with it.

What this means is that certain properties of the universe could in fact be rapidly, randomly changing right now, being experienced by us no differently than if they were not changing at all. If change were to occur, we would possess no means of being aware of that change. A universal standard can be considered to be a constant, however, in the sense that we will never detect change in the properties of the universe associated with those universal standards. Let this clarify, then, the role of the expansion of the universe as the fundamental mechanism behind the passage of time. As we have become aware, motion is a key factor concerning how time operates: we experience the motion of the hyperspherical surface of our expanding universe as the passage of time. It is this very expansion that sets the universal standard by which all time-related activity within the universe occurs. There exists, however, a factor responsible for the deviation of the flow of time from its 'universal standard' - a factor mentioned at the beginning of this section as one of the 2 main factors associated with how time operates. This factor is what we call mass.

According to the theory of relativity, mass affects the passage of time. Because this is true, each and every body found below the hyperspherical surface at the bottom of a curved sag can be considered to age more slowly than do things at the level of the surface above: the more massive the body, the more slowly it ages. What causes this deviation of the flow of time from its 'universal standard'? To understand how mass relates to the concept we call time, let us look back to how gravity works. Curved space is an element without which gravity could not exist: it is the curved shape that the surface surrounding a massive body assumes that makes the process of gravity possible. When it comes to matters of time, however, curved space operates by means of a different medium: the "stretching" of its very fabric. To better understand this, consider an example similar to the famous rubber sheet thought experiment: picture a baseball placed onto an outstretched thin latex sheet, held at its edges. Upon sinking down into the sheet, the baseball does more than 'curve' the sheet - it stretches the very fabric of the sheet.

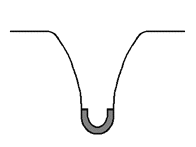
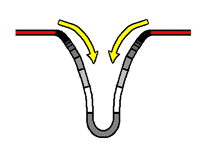
How does the "stretching" of a surface affect the passage of time? The means by which we will answer this question exists in the form of the curved sag shown in the top illustration to the right. As you can see, at the bottom of this rather steep curved sag lies a 1-dimensional massive body - a body rounded by the shape of the curved sag. To better understand how curved space affects the passage of time, we will introduce into the situation a new concept: as the surface of our hyperspherical universe expands outward, leaving behind what we understand to be the 'past' and entering into the 'future' ahead of it, what we are calling the effects of change (the time-related factors that have the potential to affect a body / object) enter directly into the hyperspherical surface, and once within it take immediate effect. A simple portrayal of the process just described can be found in the next illustration to the right. In order for the effects of change to reach a body below the level of the hyperspherical surface (at the bottom of the curved sag that surrounds it), however, the effects of change must pass through the curved space in between the body and the surface. This transition from surface to body is made possible by the effects brought upon by the constantly expanding hyperspherical surface: as the effects of change continue to directly enter into all available areas of the hyperspherical surface, the constant incoming flow of the effects of change causes the effects of change to spread out in all directions within the surface. Before long, the effects of change can be observed to have begun to move past the outer edges of the curved space surrounding the body, entering in from the level of the hyperspherical surface. Soon, the 'current' brought upon by the incoming flow of the effects of change has brought the effects of change past the outer edges of the curved space surrounding the body and down into the very curved space surrounding the body they are attempting to reach - as is shown in the bottom illustration to the right.

When the effects of change enter into the curved space, they are altered by the physical configuration of the curved space. The nature of this alteration is portrayed in detail in the bottom illustration to the right. The effects of change are "stretched out" by the very fabric of the curved space, and begin to assume a distinct 'spread out' state. This state of being 'spread out' is the mechanism behind how the flow of time deviates from its 'universal standard'. In what way does the effects of change being in this state affect the aging process of the body? Because the flow of the effects of change is reaching the body in a "stretched out" state, it takes longer for any given amount of the flow to reach the body, than if the flow of the effects of change were not "stretched out". In effect, the flow of the effects of change reach the body at a slower rate, and hence the body ages more slowly. This alteration of the flow of the effects of change can also be considered to apply to objects lying within the curved space itself (such as a clock placed there): the flow of the effects of change, having been altered, will be found to pass through any given area of the curved space at a slower rate, affecting the passage of time in that area accordingly. Take note that the more massive the body is, the more deeply it will 'sink down' into the hyperspherical surface, and hence the greater the degree to which the curved space surrounding the body will "stretch out" the effects of change.

According to the theory of relativity, objects in a state of motion undergo the passage of time more slowly than objects not in motion. The effect, however, is only noticable when the object is moving at near-light speed. Why does being in a state of motion cause this alteration of the passage of time to occur? Throughout this section, we've been made familiar with the concept of the motion of a body that exists in the form of the motion the body undergoes while being carried outward along with the hyperspherical surface of the expanding universe. The decrease in the rate of aging that can be observed to occur due to travel at near-light speed, however, deals with a different type of motion: motion of an object along a direction within the surface itself, as it expands. It is upon this type of motion that we are to focus our attention. As the means of doing so, first consider the notion that all objects possess mass. Because of this, motion of an object within a surface will always require energy / effort. The faster the rate at which the object is put into motion within the surface, the more energy / effort there will be that is required to move it. In this sense the act of putting an object into a state of motion in a direction within a surface is like increasing the object's mass: the faster the rate at which the object travels, the more massive the object can be considered to become. This answers why objects in a state of motion age more slowly: they have become more massive! In effect, the object in motion ages more slowly, for the same reasons described above explaining why mass affects the passage of time. In the same manner that a massive body was described to 'sink down' into the hyperspherical surface, the object in motion within the surface 'sinks down' into the surface within which it is travelling. The curved sag surrounding the object 'follows' the object wherever it goes, in a manner comparable to a bowling ball being pushed across a waterbed: though the object moves, the curved sag moves along with it. The faster the rate at which the object travels, the greater the extent to which the rate of aging can be considered to decrease.

The theory of relativity also states that according to a stationary observer, clocks in a state of motion will be observed to tick more slowly than clocks not in motion. We are to assume that we are that stationary observer. Understanding the current topic of discussion does not require us to go beyond anything that we've already covered. Assume that there exists a clock in a state of motion, travelling outward from us into space. This clock sends out a beam of light once every second. Because this clock is in motion, when we receive the ticks it is sending out, we measure the ticks to occur at a rate observed to be slower than the rate at which we observe the ticking of one of our own clocks that is set to tick once every second. Why does this occur? As we've been informed, putting an object such as a clock into a state of motion is comparable to increasing the clock's mass: the faster the rate at which the clock travels, the more massive the clock can be considered to become. As a direct result of the fundamental behavior of mass, the mass of the clock causes the clock to 'sink down' into the surface within which it is travelling, surrounding the clock with a 'curved sag' that moves along with the clock as the clock engages in motion. Understanding what is responsible for the observation of the ticking of a clock in motion to tick more slowly than usual involves referring to the concepts presented in the material just covered. The concept we are to address is that of how mass affects the passage of time.

As you may recall, the first step in how the rate of aging of an object in motion is decreased consists of the flow of time entering into the hyperspherical surface of the outwardly expanding universe, and spreading out into all directions within the surface. In order to reach an object at the bottom of a curved sag, the flow of time must pass through the stretched out surface of that curved sag lying in between the object and the hyperspherical surface. Once the curved sag is reached, the physical configuration of the curved sag then begins to alter the flow of time as it passes through: after having crossed the distance of the curved sag lying above the object, the flow of time reaches the object at the bottom of the curved sag in a distinct "stretched out" state - a 'spread out' version of the time-related factors entering into the curved sag from the level of the hyperspherical surface. Given the effects of this 'spread out' state, the flow of time can therefore be observed to take longer to reach the object at the bottom of the curved sag than if not "stretched out", and as a result the flow of time reaches the object at the bottom of the curved sag at a slower rate.

After putting this into consideration, we can come to the prompt conclusion that curved space has the ability to alter information passing through it. The 'information' spoken of here is, of course, the time-related factors responsible for the rate of aging of bodies and objects. What other forms could information take on? A beam of light has the potential to convey information. In fact, the beam of light that the clock described above sends out every second is information. What if the beams of light being emitted from the clock in motion once every second, themselves information, when passing through the curved space surrounding the clock in motion, behaved in the same manner that the flow of time did? We would have before us the explanation as to why the observation of clocks in motion to tick more slowly than clocks not in motion: the continuous stream of the beams of light being sent out by the clock every second, upon passing through the stretched surface of the curved sag, exits the curved sag of the clock in a "stretched out" state. The beams of light travel through space in this "stretched out" state, and upon their arrival result in our experiencing the ticking of the clock more slowly than normal. Let us further examine the factors at work: the process we know as decrease in the rate of an object's aging occurs as the result of an information-containing signal (the flow of time) entering into a curved sag. The process lying behind why clocks in motion are observed to tick more slowly than normal, in turn, occurs as the result of an information-containing signal (a beam of light) being sent out from a curved sag. In each case, the signal covers its distance across the stretched surface of the curved sag, and upon emerging altered assumes the change in properties that the curved sag has brought about.

Let us put into consideration a totally alternate situation: assume that we are in possession of a clock equal in nature to the clock in motion that we are observing. Let us assume that moving along with this clock at the bottom of its curved sag is a person observing the ticking of our clock. How would this person measure the ticking of our clock? Being stationary, we are not surrounded by a curved sag. Yet the person travelling along with the clock in motion, it would happen, measures our clock to tick more slowly than normal, even though we are stationary! How can this be? What is there to slow down the signals sent out from our clock as it ticks, if we are not surrounded by a curved sag? This is a valid argument. Everything we've covered so far has told us that observation of a clock in motion to be ticking more slowly than normal is the result of the curved sag that surrounds the clock. Yet the person observing the signal sent out from our clock measures the ticking to occur more slowly than normal. What we know, first of all, is that something in this situation is the cause of the observed slow ticking of the clock, and because the cause is not where we expect it to be, it must therefore be somewhere else. Since curved sags are responsible for observed slow ticking of clocks, the cause of the observed slow ticking in this situation must therefore be the curved sag of the person in motion with the clock observing us. This is quite possible.

You see, just as an outgoing beam of light sent out from a clock in motion at the bottom of a curved sag must first pass through the curved sag before reaching the external world, an incoming beam of light approaching an observer in motion at the bottom of a curved sag must first pass through the curved sag before coming in contact with the observer. As a result, the curved sag surrounding the observer in motion brings about the same effect that the curved sag of the clock in motion would bring out if the observer were stationary. We can therefore conclude that curved space slows down incoming beams of light in the same manner that it slows down outgoing beams. Assume, then, that our clock is sending out the signal observed from the outside as ticking. Upon reaching the curved sag of the person in motion with the clock observing us, the signal from our clock passes through the curved space that the person is surrounded by on all sides, "stretching out" the signal and presenting it to the person in an altered state.

As you may recall being stated earlier, we experience the state of constant expansion that the surface of our hyperspherical universe is engaged in as the passage of time. It is no surprise, then, that the effects of motion are the foundation upon which time operates, for time is motion. Our universe, then, is a 4-dimensional object constantly increasing in size as time goes by. What this means is that the physical size of the universe, and the passage of time, are directly related. How would one measure the size of the universe? The obvious choice is by means of the size of its radius: like the circle and the sphere, the hypersphere's lower-dimensional analogues, the distance from the centerpoint of a hypersphere to any point on its surface will always be the same, no matter what point on its surface you choose. The radius of the universe can in a sense be used as a sort of "clock", you see, that can mark specific points in time of the expansion of the universe. How, you may ask, does this "clock" work? For any given point in time during the time that the universe has been expanding, the hyperspherical radius at that point in time will be of a certain specific length. To 'access' any point in time during the expansion of the universe, we simply designate the size of the radius. This method of measurement will never fail, for the simple reason that no two instants in time will share a radius of the same length: each instant is designated a radius of a length that is unique to that instant in time.

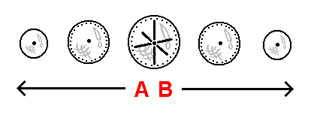How would we visualize the radius of a hypersphere? Displayed to the left are representations of the radius of a sphere, each radius presented at a right angle to the other. The sphere on top portrays the positions of each radius of the sphere as we would think of them. The sphere under the one on the top, as you can see, is in stack-diagram form and represents a Flatlander's basic understanding of how each and every instance of the radius of the sphere portrayed in the illustration above is positioned. The Flatlander is familiar with the 4 positions of the radius that occur on the central slice of the sphere - they extend parallel to the central slice itself. The remaining 2 positions of the radius, however, extend perpendicular to the central slice, and hence to the Flatlander's entire dimension. Though these 2 remaining positions of the radius extend forth in ways that the Flatlander cannot directly comprehend, the medium of the stack-diagram allows the Flatlander to grasp each radius in the form of cross-sections extending into slices that lie across multiple 2-dimensional planes.

Displayed to the left in the stack-diagram on the bottom are representations of the radius of a hypersphere, each radius presented at a right angle to the other. The hypersphere, displayed in stack-diagram form, represents our basic understanding of the positions that the radius of a hypersphere can assume. We are familiar with the first 6 positions of the radius that occur on the central slice of the hypersphere that extend parallel to the central slice itself. The remaining 2 positions extend perpendicular to the central slice, and hence to our entire dimension. Though these 2 remaining positions of the radius extend forth in ways that could be considered difficult to visualize when approached from the plane of the central slice, the medium of the stack-diagram allows us to grasp each radius in the form of cross-sections extending into slices that lie across multiple 3-dimensional planes.

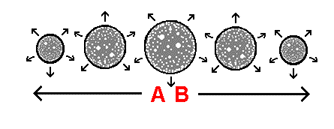
We have just completed a detailed study of how the radius of our expanding universe increases as time goes by. Having been made familiar with the concept of an expanding universe, we will now go about approaching a method of study that relates to the arrangement of bodies within an expanding universe: a concept known as the Hubble law. The Hubble law states that distances of empty space in between bodies / galaxies increase as time goes by. According to the observations that have been made of the universe around us - the very observations upon which the Hubble law is based - everything in the universe is moving away from us at a speed determined by the distance of the body / galaxy away from us: the more distant the body / galaxy, the faster the rate at which it will be found to moving away. It must be realized, however, that throughout this process of 'spreading out', the bodies will always be in a state of even distribution throughout the universe: at any time during the time that the universe has expanded (or will expand in the future), the amount of empty space found to surround any given body will in general be pretty much the same amount of space one would find surrounding any other body in the universe. What this means is that as the bodies undergo the effects of expansion, they undergo the effects of expansion in unison. In order to better understand the Hubble law, there are 2 models we will be studying that simulate the conditions related to the Hubble law as we observe them to occur within the universe. The first model informs us of the basic concept behind the Hubble law. The second model, in turn, is an attempt to explain the actual mechanism behind how the Hubble law operates.

As the means of taking part in the first model, picture a round lump of dough. Assume that we have mixed an assortment of raisins into the lump of dough, evenly distributing the raisins throughout all areas of the dough into which mixture can occur. We then roll the dough into its original rounded state, and put the lump of dough into an oven and begin to bake it. Our job as of now is to examine how the raisins distribute themselves as the dough rises. As the dough rises, we find distances in between raisins to increase in unison. To better understand this expansion, we are to focus our attention on 2 raisins on opposite sides of the outer edge of the lump of dough, and on a raisin in between these 2 raisins in the direct center of the lump of dough. As the dough rises, we find that the 2 raisins on opposite sides of the dough are moving away from each other twice as fast as either of these raisins is moving away from the raisin in the middle. The reason for this occurrence is quite simple: there is twice as much expanding dough in between the 2 outer raisins, than there is in between either outer raisin and the raisin in the middle. If we assume this relationship to apply to all of the raisins within the rising dough, then we would have before us a miniature model of our expanding universe. Upon examining the rising dough more closely, we find that from the point of view of any given single raisin located within the dough, it's as if every other raisin were moving away from that particular raisin. After further examining the expanding cluster of raisins embedded within the rising dough, we can in response to that examination conclude that there is no observable center to the expansion that is occurring throughout this enlarging cluster of raisins. Having been informed as to the basic concept behind the Hubble law, let us take this arrangement a step further.

The second model we will study addresses an aspect to the expansion of the universe not put into consideration in the first model - an aspect that is vital to the actual mechanism behind how the Hubble law operates. This approach treats the universe not as an 'enlarging solid mass' as the 'raisin' model does but as an outwardly expanding surface - a surface that surrounds the very central point away from which it is expanding. The first model was correct in its conclusion that there is no observable center to the expansion that is occurring throughout the universe. The manner in which it treated the universe as an 'enlarging solid mass', however, was a prominent error. The universe is not an expanding 'giant sphere' of empty space, but is the surface of an expanding hypersphere. As the means of taking part in the second model, we are to picture an inflated balloon. Using a marker, we place 'dots' upon the surface of the balloon in a manner that evenly distributes the dots across the surface of the balloon. We are then to deflate the balloon, and then inflate it to a state at which there is an observable spherical contour to its shape.

As the means of demonstrating the actual mechanism behind how the Hubble law operates, we proceed to continue to inflate the balloon. We are now to examine how the dots position themselves in relation to each other along the surface of the balloon as the balloon inflates. As the balloon inflates, we find distances in between dots along the surface of the balloon to increase in unison. Upon examining the surface of the inflating balloon more closely, we find that from the point of view of any given single dot located on the surface of the expanding balloon, it's as if every other dot (in terms of how they relate to the dot along the surface of the balloon) were moving away from that particular dot. As of the surface of the inflating balloon, there is no observable center to the expansion that we witness to be occurring. As with the 'raisin' model, the rate at which any 2 given dots on the surface of the balloon will be found to be moving apart (in terms of how they relate to each other along the surface of the balloon) is directly related to the distance along the surface of the balloon in between those 2 dots. In what way, you may ask, does what is described here differ from the behavior observed to occur earlier among the raisins distributed throughout the rising dough?

In the first model, the raisins were being pushed apart. In the model we are dealing with now, the dots are simply moving in straight lines. These 'straight lines' are none other than the paths that the dots follow as they move away from the centerpoint of the balloon - the point found to lie at the very center of the empty space that the surface of the balloon surrounds. As the balloon is inflated, the dots move in distinct straight lines away from this point. When the outwardly extending paths of all of the dots are brought inward, it is at the location of the very centerpoint of the balloon just described that we witness the paths of the dots to converge. This is the actual mechanism behind how the Hubble law operates: the bodies of our universe, you see, are not being "pushed apart". Rather, the increase in the empty space surrounding any given body occurs simply because the bodies are moving directly outward from their centerpoint of expansion, in the straight lines that the effects of expansion carry them. In effect, the bodies are not actually moving away from each other, but rather from the point at the very center of the expansion that is occurring - the single common point that all of the inwardly brought paths of the bodies can be observed to share.

As we are already familiar, the Hubble law states that distances in between bodies increase as time goes by. Given this reasoning, consider the following notion: if empty space in between bodies is growing (and if the radius of the universe is getting larger), wouldn't that suggest that there was a time in which there was no distance in between bodies (and no measurable radius)? Yes. The universe, at this time, existed in the form of a dense, compressed dimensionless point, and it was at this very location that the process of expansion started - an instant that can be considered to be nothing other than the beginning of time - the "big bang". At this state before the universe began, there existed no such concepts as 'expansion' or 'spreading out': motion did not exist. If we accept this as true, then neither did time exist, for time is motion.

Where within our 3-dimensional universe, then, could it be said that the event known as the "big bang" took place? The point of origin from which the universe sprang cannot, by its very own nature, be itself involved in any way with the expansion that is occurring around it: it must exist independently of the influence of anything that could be said to be expanding. As the means of better grasping this concept, let us return to the 'models' of the Hubble law presented earlier. Let these two models represent 2 different conceptions of our expanding universe. Both models, as one can see, are 3-dimensional expanding spheres. The first model - the 'raisin' model - is solid. The second model - the 'balloon' model - is hollow. The type of cosmos each model represents is observably different from the other. Both spherical models, being spheres, possess a 3-dimensional spherical centerpoint.

In the 'raisin' model, this centerpoint exists at a location occupiable from within the cosmos that the model represents - the centerpoint physically lies within that cosmos. In the 'balloon' model, however, the status of the spherical centerpoint is different: the centerpoint lies in a location unreachable from the cosmos that the model represents - the centerpoint is physically external to that cosmos and is surrounded on all sides by the surface moving outward from it. Assume, then, that we have the task of designating the point on the surface of the balloon that best portrays the location of the balloon's centerpoint. Upon attempting to perform this task, it becomes quite clear that designating the location of the balloon's centerpoint by means of a location on the surface of the balloon is impossible. We are now to apply this to our own universe. No occupiable location within our universe can successfully designate the location of the universe's hyperspherical centerpoint - the very point at which the "big bang" took place. Determining the location of the hyperspherical centerpoint of the universe is in essence impossible, when the attempt to refer to the hyperspherical centerpoint is made from within the hyperspherical surface that surrounds it! As you may recall from an earlier section, it is impossible to relate to the external configuration of a surface that you yourself exist within.

To answer the question of where within our 3-dimensional universe the event known as the "big bang" took place, we must view the hyperspherical surface of our universe as it appears from outside its boundaries. The stack-diagram presented below represents such an approach. The centerpoint of the hypersphere - at the centerpoint of the hollow central spherical slice - is fixed: it is the very distinct, very defined point of origin from which the universe sprang. As can be seen by observing the expanding surface of the hypersphere, there exists no single point within that surface that could be said to be the center of the expansion that is occurring - which is in precise accordance with the rules set down by the Hubble law. Bodies within the hyperspherical surface are not being "pushed apart" as one would conclude based upon the reasoning of the 'raisin' model (a manner of reasoning typical of an attempt to relate to the bodies from within the surface in which they lie). Rather, the increase in the empty space surrounding any given body occurs simply because the bodies are moving directly outward from their centerpoint of expansion, in the straight lines that the effects of expansion carry them.