Area of Mandelbrot Set Components and Clusters

© by Jay R. Hill, August 18,1997

The area lower bound passes 1.5063036.

The area of the Mandelbrot Set is one of those useless measures which, since it exists, some feel compelled to determine. If this were too easy, we would quickly move on to other things. In my chapter in Fractal Horizons: The Future Use of Fractals,(Cliff Pickover), editor (St. Martin's Press, 1996) I reported the lower bound is 1.50585063. This article reports the area evaluation of 430809 components of the Mandelbrot Set yielding an improved lower bound of 1.506303622. In Table 1, the areas of components and clusters are summarized for components with periods 1 through 16. The second column shows the total area of all components with the period shown in column one. The third column shows the total area in clusters whose base 'cardioid' has the period in first column. The last column shows the total number of components used to evaluate the cluster areas.

 Table 1. Area of components and clusters by period
Period Area in Components Components 
in Period		 Area in Clusters Components 
in Clusters
1
 1.1780972450961724644
1
 1.50503855428823502
147367
2
 0.1963495408493620774
1
 0.0
0
3
 0.0565424181276813797
3
 0.000509098755090629897
9537
4
 0.0232751376963008120
6
 0.000207642997261544123
7777
5
 0.0131150674788924099
15
 0.000154964697691598031
14958
6
 0.00893479053124321716
27
 0.000085410730163877997
12524
7
 0.00505792907074769483
63
 0.000067726232188880309
21079
8
 0.00446801353800303623
120
 0.000052940923971230971
20290
9
 0.00293643139498573089
252
 0.000043683578270399760
23256
10
 0.00266092631691072575
495
 0.000029533275741775911
20431
11
 0.00138279912887913744
1023
 0.000024292549681291682
26398
12
 0.00210143991593237747
2010
 0.000029737257658746096
18985
13
 0.00085107478579664163
4095
 0.000015032630104988673
24074
14
 0.00113392232036243556
8127
 0.000014189857813159913
23320
15
 0.00094487534275074597
16365
 0.000018402872562644416
26624
16
 0.000892812353050448
32640
 0.000012411370977807982
34189
Total
 1.498744423947071128
65243
 1.506303622017414
430809

Method of area evaluation

The area of the Mandelbrot Set question has been discussed at length on the internet (sci.fractals) for several years. Here are some of the evaluations methods. [email messed up to foil spam, remove XXXX] My current approach to computing the area calculations uses three steps. For background information, see my chapter in Fractal Horizons : The Future Use of Fractals,(Cliff Pickover), editor (St. Martin's Press, 1996).
  1. Locate the centers of all 'cardioid' components of each period
  2. Recursively locate the centers of all attached 'bud' components
  3. Evaluate the areas of each 'cardioid' and its 'bud' components
In that paper I report the lower bound as 1.50585063. This article reports a new greater lower bound, within about .013% of statistical area estimates (1.506539, Munafo, sci.fractals, 17 Oct 1996) or  0.019%  (1.50659177 ± 0.00000008, Munafo, 4 Feb 00) or 0.012% (1.506484 ± 0.000004, Kerry Mitchell, 2001.

The values for component areas with periods 1 through 16 are believed to be correct to about 10-17, since verification of period 3 components using a different method agrees to that accuracy. The number of roots for period p is 2p-1 less the total in periods which are factors of p. For example, to evaluate the total area in period 15 required evaluating 7,077 roots! Notice that when p is prime, the area is relatively smaller. This is because some of the components of composite periods are attached to large components of lower period (factors of p).  An example is the period 4 component at -1.3107026413 (part of the period 1 cluster) which is 20 times the area of the period 3 cardioid.

Each component is the base of a cluster of attached buds. The area of the complete cluster (to some limit) has been evaluated by recursively locating and evaluating buds around each cardioid. With this calculation, the total area comes to more than 1.5063036. For example, to evaluate the area for period 15 clusters required evaluating 26624 components! For each cardioid with period less than 17, the corresponding cardioid cluster area was recursively evaluated, stopping with bud periods greater than 256, or when the bud radii were smaller than 10-5.

Note:  A word about period 16.  There are 32640 components of period 16. That is, 128 less than 215 since there are 128 components with periods 1, 2, 4, and 8. This corresponds to roots of the 215 degree polynomial one gets when you iterate the Mandelbrot Set formula 16 times that are of lower period. I have located all roots but one (the search for it continues). So the values in the table are close but less than the total area in period 16.

Can we extrapolate the areas to higher periods?

It looks like the cluster areas may be an exponential function of period. Here is a plot of cluster area vs. period. To avoid logarithm errors for period 2 which is not a cluster (it is part of the period 1 cluster), I have replaced its 'cluster' area with its component area. The figure shows a log plot of the area vs. period.

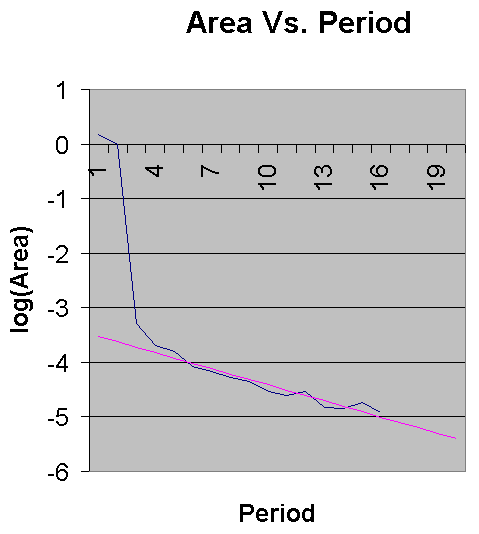
The curve settles to a roughly straight line. Using least squares log fit to the cluster areas in periods 4 through 16, I get A=3.687199´ 10-4´ 0.79833p. The intercept is accurate to about 16.2% and the standard error of the 'slope' (0.79833) is 0.01833.  This model can be evaluated for p>16, summed and added to the total we have through period 16.  I get 1.50633534 ± 0.0000335. This is still significantly less than Robert Munafo's value (1.50659177 ± 0.00000008). This gap may or may not be closed with additional component evaluations. There are two sources for additional area, one, evaluating the clusters to higher periods and two, accurate measures of clusters above period 16.

Updated Sept 18, 2003.

[Home][Home]

1

Hosted by www.Geocities.ws

1