The price a manufacturer charges for widgets, like the pricing policy of any other business, needs to cover costs and give a profit. Otherwise why build widgets? We will allow our company to make after tax profits of 5% of sales. This may not be enough to encourage the company to remain in business, but that is all this company makes. The company makes and sells one hundred thousand widgets a year.
With a starting price of $10,000 per widget that gives $1 billion -- $10,000 per widget times one hundred thousand widgets per year -- in total annual revenue. A 5 percent profit is $50 million a year. Corporate income taxes take another $50 million of the total revenue. Since the $100 million profit and taxes comes from the $1 billion in total sales the remaining $900 million is the cost of building widgets. The cost of labor to produce 100,000 widgets is $750 million. This may seem high, but it includes $150 million -- 20% of $750 million -- of personal income taxes taken from the workers leaving them meaningful wages of $600 million. Also, there is no material cost to build widgets. All the materials come from an inexhaustible well in the factory that was part of the cost of the factory. This cost is $150 million a year to pay the economic interest on the factory.
The cost of the factory was actually $1 billion. However, the factory is indestructible and the very best of technology. It will never wear out, it will never become obsolete and it also includes that inexhaustible well mentioned earlier. To pay for this factory the $1 billion was borrowed in a very special way. The economic interest is 15 percent and nothing is paid on the principle. It will take a long time to repay. But then the factory never wears out nor can it become obsolete. Fifteen percent of $1 billion is $150 million per year to maintain ownership of the factory.
This is the way things are at the start of our analysis. It tells us nothing of why the price is $10,000 but we are aware of something about the effect of price on sales.
The price is set by the company so that it can make the most profit possible. An increase in price would increase the revenue for each widget sold. There would be fewer widgets sold and the cost of producing fewer widgets would be less. A reduction in price would cause increased sales and the costs to produce more widgets would be greater. But which price change, if either, will give the most profit?
The simple truth is that we do not know which direction, or even if, the price should be changed in order to make the most profit. A price increase will reduce sales. But will it reduce sales more or less than it reduces costs? A price decrease will increase sales but will it increase sales more or less than it increases costs?
The only way to determine this is with the empirical method described earlier in the analysis of the monopoly tax. A price increase can be tried and if profit goes up another increase can be tried until the maximum profit is attained. Each time the price is raised fewer widgets are sold and fewer workers are needed but, because both revenue and costs change with a price increase, profits can either increase or decrease. If profit is reduced by a price rise the price can be lowered to see what happens. When the price is reduced more widgets are sold and more workers are needed to make the widgets, again affecting both cost and revenue. To determine profit it is necessary to understand how changes in costs and revenue are affected by production.
One way is to reclassify costs as either fixed costs or variable costs rather than the labor, capital, economic interest and tax costs listed earlier. Economists have also defined this kind of classification. They define fixed costs as those that do not change with the quantity produced and variable costs as those that do. It is interesting to note that it can also be said that the opposite is true.
That is, economists say a fixed cost is one in which the total cost of production does not change with an increase in production but, because the unit cost is the total fixed cost divided by the number produced, that means that the unit cost of production from such a cost does vary with production and it could just as well be called a variable cost. Likewise, economists define variable costs as those that the total cost varies proportionately with production because the unit cost is fixed and the total cost becomes the unit cost times the number produced.
To avoid confusion with this terminology we will call the costs economists call fixed -- monopoly costs. They are the costs associated with maintaining monopoly (ownership) of the production capability -- the factory and the right to produce. Variable costs -- the costs associated with actual production -- we will call manufacturing costs.
When this company was introduced the costs of building 100,000 widgets was $50 million for corporate income taxes, $150 million for personal income taxes, $600 million for labor and $150 million to maintain ownership of the factory and the rights to produce widgets. This left a profit of $50 million.
The first of these to be analyzed is monopoly costs. Ordinarily monopoly costs (i.e. -- The costs incurred to maintain control of the means of production.) involve a lot of complicated computations to cover such expenses as the labor and material needed to protect the factory from the weather and vandals, labor and material costs to fix wear and tear from use, amortization to recover the investment cost, etc. That is why the widget factory has been simplified. These calculations are avoided by making the factory indestructible and the best technology. (It also helps to have that inexhaustible well in the factory floor included as part of the factory cost instead of buying little pieces of all the mines, farms and factories that produce the material from which widgets are made.) This eases the accounting of monopoly costs. That is, monopoly costs are costs that are incurred regardless of how many widgets are made. They are incurred even if no widgets are made.
Corporation taxes as now imposed are measured by profits, not the privilege of ownership, and are therefore not monopoly costs. Likewise, labor costs including the personal income taxes paid for the production of widgets are not part of the cost to maintain ownership of the factory. Profits are not costs so they are also not monopoly costs. Monopoly cost for our model widget factory includes only the $150 million economic interest paid to control (own) the factory.
Next we will consider manufacturing costs. These consist of the costs incurred to actually build widgets. Total revenue is $1 billion. One hundred and fifty million dollars has now been accounted as monopoly costs, leaving $850 million as yet unaccounted. Economists would say there are only these two kinds of costs. But, is that really so?
We have already ascertained that corporate income taxes are not monopoly costs because if no widgets are made there are no taxes. But it is also true that if no profit is made there will be no corporate income tax no matter how many widgets are made. Profits and the associated corporate income taxes are not proportional to the number of widgets made so they are not manufacturing costs as we have defined them. Therefore the manufacturing costs are only the $750 million of labor and personal income taxes that are approximately proportional to the number of widgets made. (We will address profits and corporate income taxes a little later.)
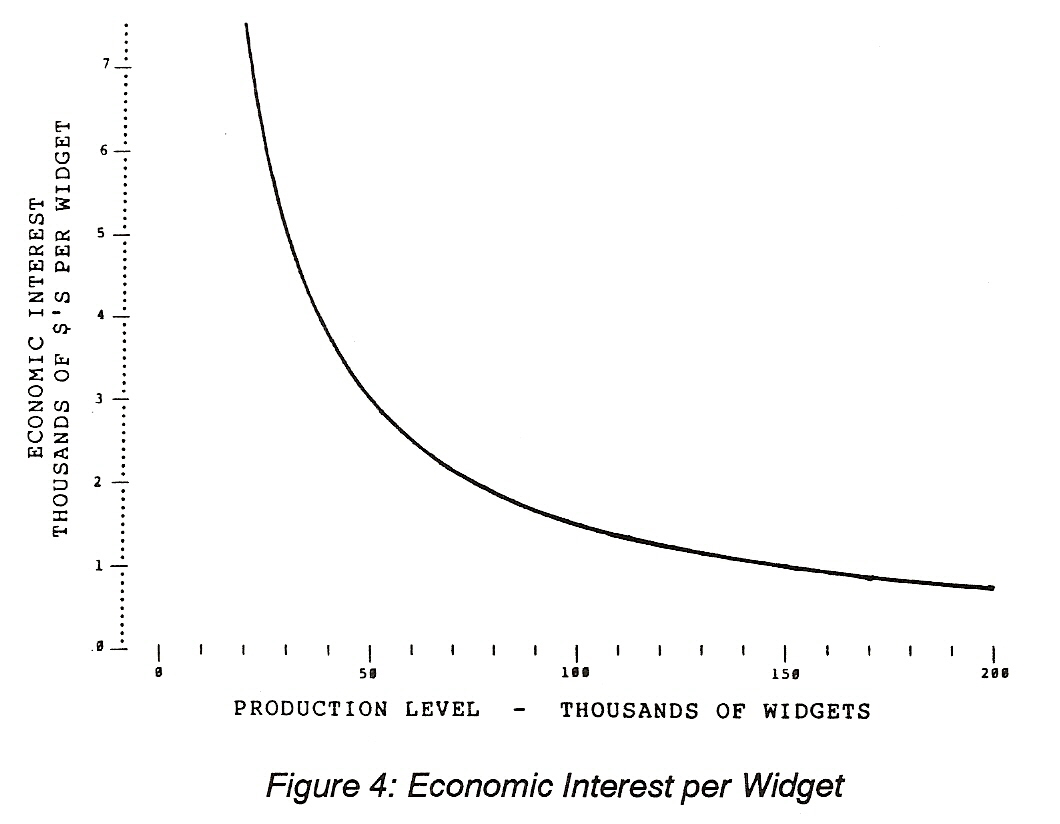
Next we will consider how these various costs are affected by production. Again, we will consider monopoly costs first. The peculiarity of monopoly costs is that they do not change no matter how many widgets are produced but, the amount of this cost accountable to each widget made does change. [NOTE: This is an oversimplification, but it does make the computations easier. -- jbod] That is, if only one widget per year is made the monopoly cost attributable to that widget is $150 million, if two widgets are made each must cover $75 million of the fixed costs to maintain the monopoly and if one hundred thousand widgets are made the monopoly cost is $1,500 per widget. The monopoly costs per widget for various production levels are shown in Figure 4.

Declining cost with increasing production is one of the effects of what economists call the law of variable proportions, which is one of the factors in economies of scale. This law is called the law of variable proportions because the size of the factory is not changed every time the number of widgets made changes. What is done is more workers are hired as the demand for widgets rises. However, widgets are produced less efficiently if either more or fewer workers are employed than is appropriate to the design capacity of the factory. That is, the proportion of labor cost relative to monopoly cost is changed.
The law of variable proportions is that there is one best proportion of inputs -- capital and labor -- to produce the lowest total cost. With any other proportion of these inputs the cost will be higher than with this best proportion. We will have more to say about this economic law after we examine the effect of production on manufacturing costs.
We have used the economists definition of variable costs for what we are calling manufacturing costs. We, like the economists, have idealized this definition just like we have idealized the definition of monopoly costs. That is, we have said that they are costs that are proportional to the level of production. This is not precisely correct. However, it is an acceptable approximation within a reasonable range of the production capacity of the factory but not so at extreme deviations. For example, the efficiency of producing one or two widgets in the widget factory would certainly not be very high. Neither would producing 200,000 widgets.
The inefficiency of producing too few or too many widgets economists call diseconomy of scale which is, of course, the opposite of the economies of scale mentioned earlier. The causes of diseconomies of scale when too few widgets are made is the higher unit monopoly cost and the loss of the efficiency of an appropriate division of labor.
Adam Smith told us about the efficiency gained by division of labor in his 1776 epic The Wealth of Nations. The division of labor is not substantially hindered by small changes in production level. This effect is not of much concern here. But diseconomies of scale from building too many widgets is the motivation for investment in new and bigger factories and is of considerable interest as is building to few which results in the factory closing.
The motivation for additional investment is that profits can be increased by reducing the costs of production and if more widgets can be sold it only makes sense to invest in a more appropriate factory so they can be built more cheaply.
It is sometimes helpful to look at things from another perspective. The law of variable proportions is also called the law of diminishing returns. To build more widgets more workers are hired. As more workers are hired the average cost of producing widgets becomes less until we approach the capacity of the factory. When the production level reaches the design capacity of the factory -- the point of diminishing returns -- more widgets can be built. That is, if we push more workers into the widget factory we can build more widgets. The trouble is that each widget will cost more to build.
This is because the workers do not have enough machines and the materials cannot be processed efficiently. As a result there are diminishing returns for each added unit of labor. Thus, the law of diminishing returns. Our factory has been designed for 100 thousand widgets per year.
Beyond the point of diminishing returns manufacturing costs increase. We do not know how much they increase so we will make an assumption based on the obvious nature of this increase. The increase will be exponential because the further we move past the design capacity of the factory the greater will be the inefficiency. That is, building a few more widgets will not have much effect on efficiency but trying to gain even a small percentage increase in production causes a noticeable increase in cost and trying to double the number would be almost impossible. The labor cost inefficiency is shown graphically in Figure 5.
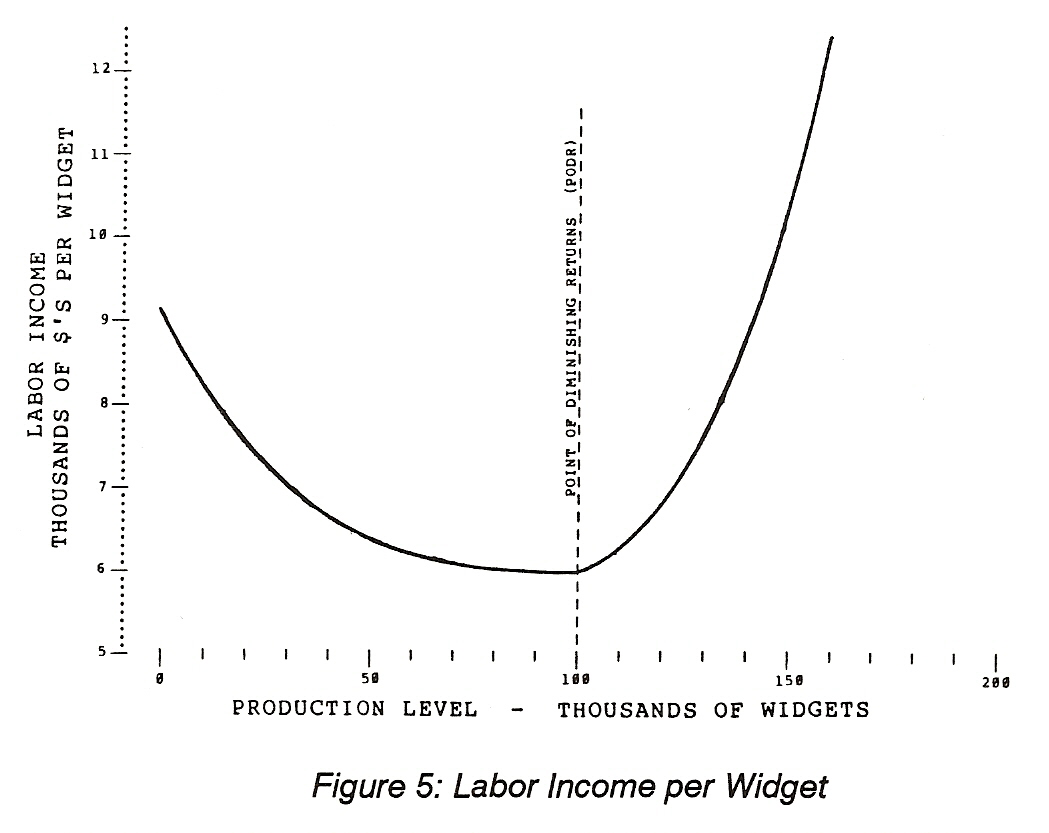
For our example the labor cost at the point of diminishing returns is $6,000 per widget with only insignificant changes immediately below that point. Above the point of diminishing returns costs increase slowly at first and then quite rapidly.
Personal income taxes of 25% (20% of the total of labor cost plus the tax.) are then added to the accumulating total. [NOTE: For those interested in the technical details, the complete model of this factory, including the equations used to create all the schedules depicted in these graphs, is in the appendix.]
The last cost to be considered is the corporate tax that is neither a monopoly cost nor a manufacturing cost. This cost is proportional to profits so we now must see how profits change with production.
Before-tax profits per widget are, of course the difference between the costs -- monopoly plus manufacturing -- and the revenue -- the sales price. To determine the profit we must establish the sales price.
The price of $10,000 per widget causes both supply and demand to be 100 thousand widgets per year. We have also established that a higher price will cause reduced sales and a lower price will cause increased sales. To account for this obvious phenomenon we will assume that the industry is very competitive and sales are changed by 250 widgets for each 0.025% change in price and the change is uniform throughout the range of prices that are relevant to our example.
Corporate income taxes are 50% of the difference between revenue (price) and costs other than the corporate income tax. These are all shown on the complete supply-demand schedule in Figure 6.
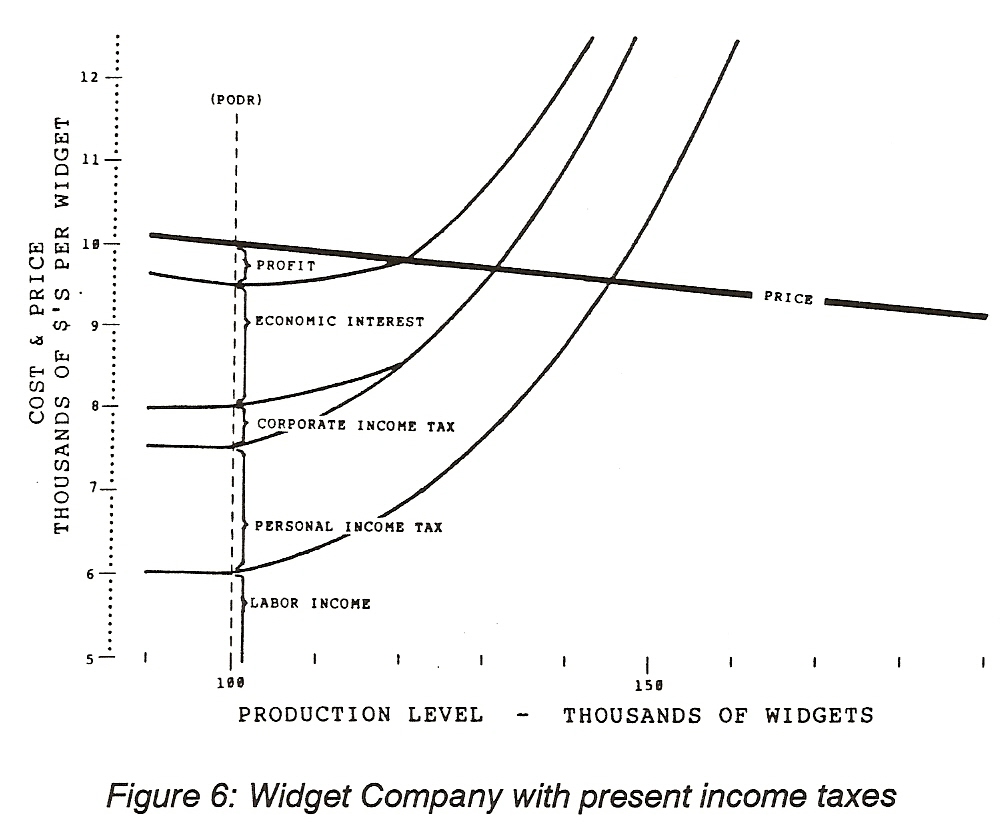
The point of maximum profit for producing widgets as the system is now structured occurs at the ponint of diminishing returns and consists of the profit per widget -- in this case $500 -- times the number of widgets sold -- 100,000 -- a total of $50 million. Taxes consist of $50 million in corporate income taxes plus $150 million in personal income taxes, labor income is $600 million and economic interest is $150 million accounting for the total revenue of $1 billion equal to 100,000 widgets bought and sold at $10,000 each.
The next step in our analysis is to change the tax system from personal and corporate income taxes to the monopoly tax. To see how this affects the production of widgets and the revenue distribution compared to the existing tax system we will start by collecting exactly the same amount of tax as with the present system -- $200 million -- at the same level of production and at the same price with the same income to labor and the same amount of profit. Because this tax is a charge to the owner of the widget factory independant of how many widgets are made it does not change with production. The cost per widget does, of course, change.
Because the owner seeks to obtain the most profit possible, when the tax system is changed the price is adjusted up if that will give more profit or it is reduced if that will do the job. In this case the job is done by reducing the price to $9,960.05 as is shown in Figure 7.
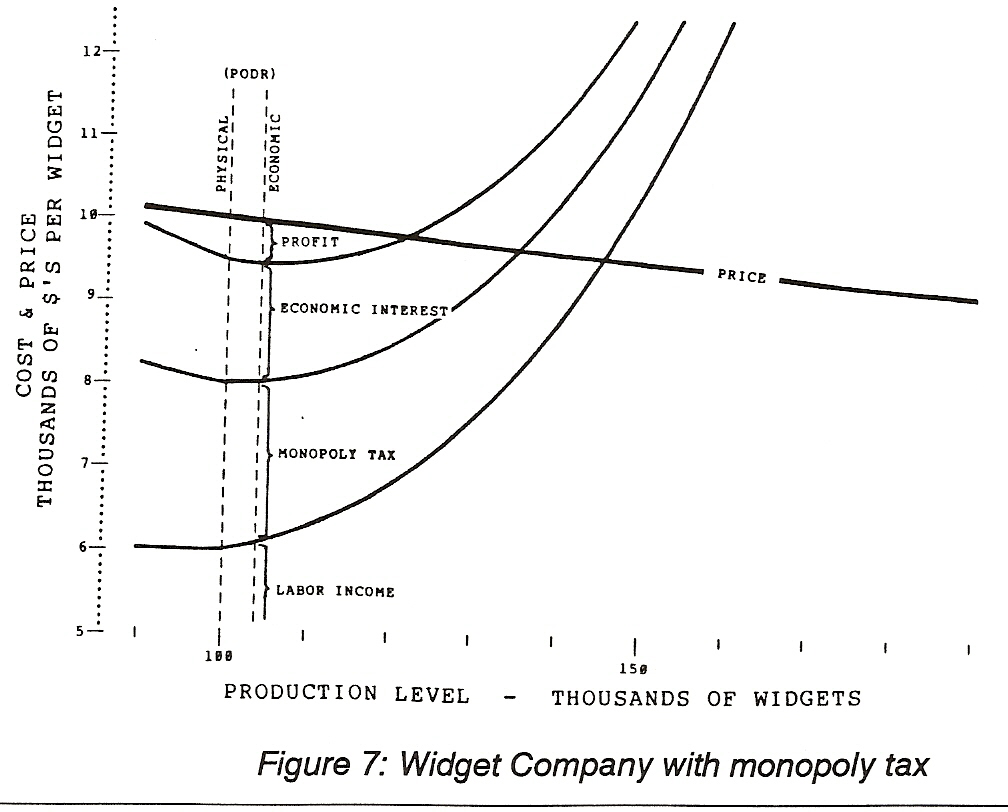
[NOTE: The increase in labor costs from $6,000 each to
$6,094.346 is because of the loss of efficiency from
production above the point of diminishing returns.]
An interesting thing about this monopoly tax is that it can be increased to any amount and the production level for maximum profit does not change. For example, if the tax is raised to take all the profit as is shown in Figure 8, the production at maximum profit is still 104,000 widgets. That is, any other production level, including zero, results in a loss rather than the zero profit that occurs with producing 104,000 widgets. The only thing is -- Will people be willing to invest in widget factories if there is no profit?
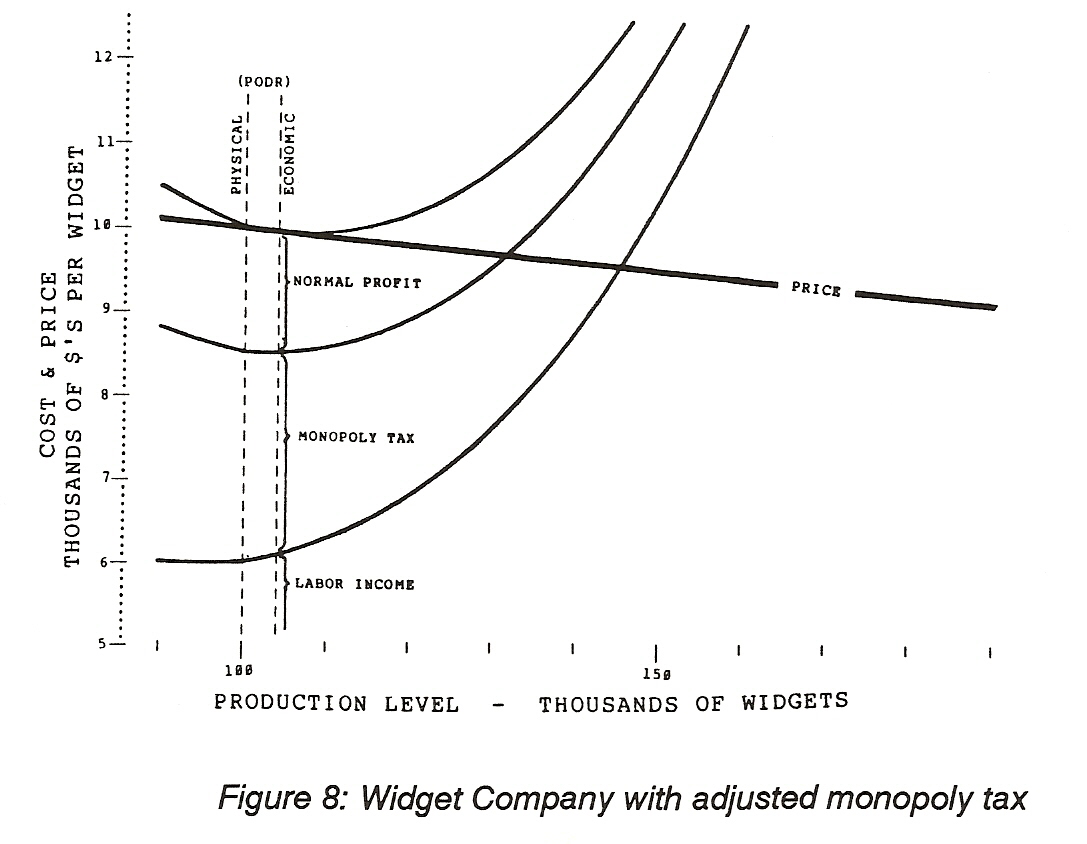
Economists address the problem of encouraging investment by recognising that a normal profit is essential to cause people to invest in productive capacity. They call normal profit a cost in order to distinguish it from what they call monopoly or economic profit that comes from the ability to set the offered for sale price of widgets. They do not have any idea how much this normal profit must be. I do not either. This problem is why the optimum amount of tax can only be found by the trial and error method described in Step 2 - Taxing Monopoly. That is, if the tax is too high people will not invest. If it is too low, labor and management fight over the spoils leaving consumers to pay higher prices. If it is just right, either an increase or a decrease in the tax will cause maximum profit to occur at a higher price with its associated lower production. That is the essence of why the monopoly tax causes economic growth to be maximum when the tax rates are optimized.
There is, however, one thing about normal profit that I do recognize. That is that normal profit is the same as economic interest as it is defined by economists. They say, as was stated in the Introduction - Cause and Effect, economic interest is the charge for the use of capital, not the charge for use of money. Normal profit is like a charge for the use of capital. It is the share of revenue needed to cause people to own and invest in productive facilities.
The cost of the factory was assumed to be 15% economic interest on the $1 billion price of the factory. The cost of the money borrowed -- the ordinary interest -- was not stated. The relationship of ordinary interest to normal profit is also indeterminate as to amount, but is obvious as to the effect of the difference.
Any time ordinary interest is greater than normal profit investment will cease. Greater earnings at less risk and effort can be made by lending money than by purchasing capital. If interest and profit rates are close investment will be reduced because many potential investors will perceive the slight difference in revenue as insufficient to take the risk of loss if their guesses of the value of investment might be wrong.