小素民族
![]()
威爾遜素數
英國數學家威爾遜 (John Wilson 1741-1793) 爵士在其給另一英國數學家華林 (Edward Waring 1736-1798) 的信中提及一個素數判別法則,詳見《沒人會用的判別法》一文。
我們把威爾遜定理 (Wilson's Theorem) 即:(p-1)!-1 = 0 (mod p) ,式中 (p-1)! 為 (p-1)的階乘 (Factorial) ,即是 (p-1)*(p-2)*(p-3)*...*3*2*1,p為一素數。上式是指對所有素數 p, (p-1)!-1 皆可被 p 整除。但當除以 p2 又怎麼樣?若符合,即
(p-1)!-1 = 0 (mod p2)
我們便稱此類素數為威爾遜素數 (Wilson Prime)。數學家簡迪爾 (Richard Crandall 1947- ) 、迪切爾 (Karl Dilcher) 及 波門倫斯 (Carl Pomerance) 在 5*108 以內搜索,只發現 5、13 和 563 三個威爾遜素數 (OEIS A007540 ) 。
![]()
威費希利素數
威費希利素數 (Wieferich Prime) 即一素數符合下式:
2p-1 = 1 (mod p2)
其實這是費馬小定理 (Fermat's Little Theorem) ,即 2p-1 = 1 (mod p) ,的一個特例。
早在 1909年,德國數學家威費希利 (Arthur Wieferich 1884-1954) 證明: x, y, z 是整數同時 p 是素數使得 xp + yp + zp = 0,並且 p 不能整除 xyz,那麼 p 就是威費希利素數。
對費馬小定理而言,所有奇素數皆符合;但不是所有奇素數皆是威費希利素數。數學家簡迪爾、迪切爾 及 波門倫斯 只發現了 1093、 3511。這是在 4*1012 中惟一的兩個例子 (OEIS A001220)。
特別地,數學家把發現這兩個僅有的例子有一些共通點:在它們減去 1 的偶數的二進制表示式中找到某一程度的規律。
1092 = 100010001002
3510 = 1101101101102
未知這是巧合,還是威費希利素數一必然特性。畢竟這類素數太少了,我們實難定斷。
別的數學家把這定義擴充,不限以 2 為底,任何素數也可為底:
pq-1 = 1 (mod q2) 及 qp-1 = 1 (mod p2)
若上兩式同時對素數 p 及 q 成立,則 (p,q) 稱作雙威費希利素數對 (Double Wieferich Prime Pair) 。現在知道的例子僅有:(2, 1093), (3, 1006003), (5 , 1645333507), (83, 4871), (911, 318917) 及 (2903, 18787)。
數學家米赫利斯古 (Preda Mihailescu) 指出在找尋卡塔蘭 - 丟番圖問題 (Catalan's Diophantine Problem) xp - yq = ± 1 的解時,x、y 為整數且 p、q 為大於 3 的素數,這 (p,q) 必為雙威費希利素數對。
![]()
胡斯頓賀姆素數
1862 年,英國數學家胡斯頓賀姆 (Joseph Wolstenholme) 證明了一個有趣的結果:
若 p 為不少於 5 的素數則 由 1 至 p-1 的倒數和的分子可被 p2 整除;
而另一方面,由 1 至 p-1 的平方倒數和的分子則可被 p 整除。
這一性質為所有不少於 5 的素數均符合,但若我們把模的次方提高一次的話,便得下式:
![]()
所謂胡斯頓賀姆素數 (Wolstenholme Prime) 是指一素數若乎合上式。
這是關於中心二項式系數 (Central Binomal Coefficient) 的。
或等價於:
![]()
其中上式中的 Bn 為第 n 個伯努利數 (Bernoulli Number),
![]()
當一素數 p > 7 時,該素數若為胡斯頓賀姆素數須符合下式:
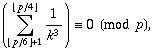
但可惜至今,我們只知有 16843 和 2124679 兩個胡斯頓賀姆素數 (OEIS A088164),其中 16843 是由塞爾弗里奇 (John L. Selfridge 1953- ) 和 保歷克 (Pollack) 於 1964年找到的,而 2124679 則是由簡迪爾 (Richard Crandall)、埃華爾 (Reijo Ernvall) 及 米辛基拉 (Tauno Metsqnkyla) 於 1993 年發現的。
數學家麥因杜殊 (Richard McIntosh) 已證在 109 內沒有其他胡斯頓賀姆素數,但他卻猜想有無限多個胡斯頓賀姆素數,但證明可不易。
![]()
迪蘭尼素數
迪蘭尼數 (Delannoy Number) D(a,b) 是指由 (0,0) 至 (a,b),只可向上、右或右上方向走的可行路徑數。
如 D(2,2) = 16
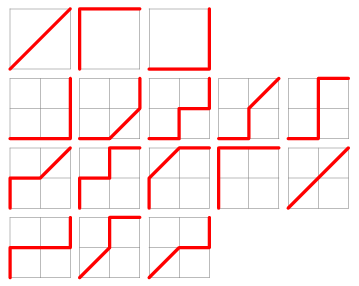
其實我們有一遞推公式 (Recurrence Equation) 求出迪蘭尼數:
D(a,b) = D(a-1,b) + D(a, b-1) + D(a-1,b-1) 其中 D(0,0) = 1
求出迪蘭尼數亦是初中、高小數學競賽中常見的問題。
若取 a = b = n 的話,我們稱作中心迪蘭尼數 (Central Delannoy Number) 的一數列: 3, 13, 63, 321, 1683, 8989, 48639, ...... (OEIS A001850)
其中的素數,即中心迪蘭尼素數 (Central Delannoy Prime) 或迪蘭尼素數 (Delannoy Prime),首 11000 個迪蘭尼數中就僅有 3, 13, 265729 三個素數 (OEIS A902830) 。
![]()
莫斯堅素數
莫斯堅數 (Motzkin Number) 的定義和迪蘭尼數相若,不過這次是考慮由 (0,0) 至 (n,0) 的可行路徑數,但只可向右上、右下或正右方向走,這簡記為 M(n) 或 Mn。
如 M0 = 1, M1 = 1, M2 = 2, ....
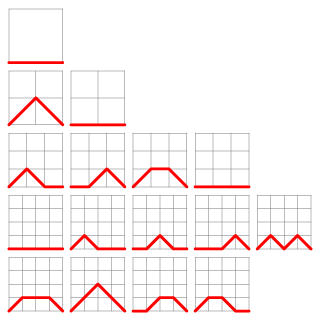
我們可以用一遞推公式求出莫斯堅數:
Mn = (n+2)-1 * [3(n-1)Mn-2 + (2n+1)Mn-1]
其中 M0 = 1, M1 = 1。
其中的素數,即莫斯堅素數 (Motzkin Prime) ,首 263000 個莫斯堅數中就僅有 2, 127, 15511, 953467954114363 四個素數 (OEIS A902832) 。
參考文獻及網址:
Guy, R. K. §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Ribenboim, P. "The Little Book of Bigger Prime" , New York: Springer-Verlag, 1991
Ribenboim, P. "Wieferich Primes." §5.3 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 333-346, 1996.
Ribenboim, P. "Wilson Primes." §5.4 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 346-350, 1996.
Weisstein, E. W. "Bernoulli Number." From MathWorld. http://mathworld.wolfram.com/BernoulliNumber.html.
Weisstein, E. W. "Delannoy Number." From MathWorld. http://mathworld.wolfram.com/DelannoyNumber.html.
Weisstein, E. W. "Double Wieferich Prime Pair." From MathWorld. http://mathworld.wolfram.com/DoubleWieferichPrimePair.html.
Weisstein, E. W. "Motzkin Number." From MathWorld. http://mathworld.wolfram.com/MotzkinNumber.html.
Weisstein, E. W. "Wieferich Prime." From MathWorld. http://mathworld.wolfram.com/WieferichPrime.html.
Weisstein, E. W. "Wilson Prime." From MathWorld. http://mathworld.wolfram.com/WilsonPrime.html.
Weisstein, E. W. "Wilson Quotient." From MathWorld. http://mathworld.wolfram.com/WilsonQuotient.html.
Weisstein, E. W. "Wolstenholme Prime." From MathWorld. http://mathworld.wolfram.com/WolstenholmePrime.html.