數獨的數學

 

最小數獨問題

數獨 (Sudoku) 是近期風行全港的填寫式數學玩意，可動腦筋，在繁忙的都市生活中帶來一丁點新情意。

所謂數獨，是在一給定的 9x9 的方陣中的空格上填上 1 至 9 這 9 個數字中其中一個，使每一直行、橫行及九個 3x3 的小方陣中均有 1 至 9 的數字各一。

 

數獨始於 1979年，由一位叫卡因斯 (H. Garns) 的人提出，且刊登於他的一本數學問題集中。後來問題流傳至日本且被發揚光大。其實數獨的問題和拉丁方 (Latin Square) 不無關係。所謂拉丁方，即把 N 個數字填在一 NxN 的方陣中，使每一直行、橫行上均有 N 個不同的數字。當然數獨的要求比九階拉丁方要求更高，我們也可把之視作九階拉丁方的特例。

九階拉丁方有多少個？數獨又有多少不同的款式？

首先我們得知在拉丁方中，數字本身並無特別意思，即 1 和 2 並無分別。故任意的行列互換或數字對換也會成為拉丁方，這兩個拉丁方我們只視之為一。在數獨上可有點不同，但原則相若，若可經過行列互換或數字對換而成的新數獨，我們也視之為一。

那麼有多少？九階拉丁方有 377597570964258816 個之多，數獨也有 5472730538 個之多，但若把經過行列互換或數字對換而成的新數獨都計算在內的話，則有 6670903752021072936960 之多。

我們填解數獨，所以重的方法不外是看看每一格的可能數值，把答案可能個數較少的先填，再以推測、試錯等方法把沒有可能的答案剔除，重而得解。

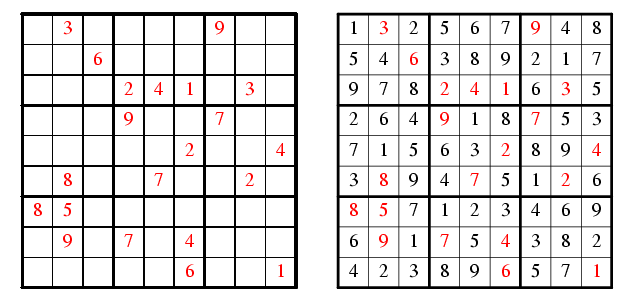
有數學家借題發揮，利用數獨找尋更大的數學思考空間。如有人問：我們要給定最少多少個數字才可使數獨的答案是唯一的呢？數學家萊利 (G. Royle) 發現了 30000 個給定 17 個數字的數獨可給出唯一的答案，而 16 個數字的則找不到一個可給出唯一的答案。但這只能使我相信最小數獨問題 (Minimum Sudoku Question) 是答案很有可能是 17 ，但未經證明。而本人亦相信此三萬個給定 17 個數字的數獨應該也是數獨中最難的問題了，故順手牽羊牽來三個給網友解解看。 (我本人沒有答案的)

 

 
 
 
 
 
 
 
1
 
4
 
 
 
 
 
 
 
 
 
2
 
 
 
 
 
 
 
 
 
 
 
5
 
4
 
7
 
 
8
 
 
 
3
 
 
 
 
1
 
9
 
 
 
 
3
 
 
4
 
 
2
 
 
 
5
 
1
 
 
 
 
 
 
 
 
8
 
6
 
 
 
 
 
8
9
 
 
 
7
 
 
5
3
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
7
6
 
1
 
 
 
9
 
2
 
 
 
 
 
 
 
 
 
 
 
 
8
 
 
 
 
 
 
 
 
2
 
8
 
5
4
 
 
 
 
7
 
 
 
 
 
 
 
 
 
3
 
 
4
 
 
5
 
 
7
 
 
 
5
 
 
 
 
1
 
 
 
 
 
 
 
 
 
 
 
 
 
 
2
 
 
 
3
4
 
 
1
7
 
 
 
 
 
 
8
 
 
 
 
 
 
 
3
 
 
 
 
4
 
6
 
 
 
 
 
1
 
 
 
5
 
 
 
 
8
 
 
 
 

 

數獨可以是一個動腦筋的遊戲，但也可以是數學科的研習課題，這只取決於我們怎樣利用這工具。

 

我的解數獨方法

我閒來也玩玩數獨，說快也不算快，報刊的數獨問題也得花上十多分鐘才解得答案。

不過我也希望把我用的方法拿來討討論論，若有高人，不妨指點點。

 

推線法

以下數獨為例：

 
6
 
 
1
9
8
 
2
5
 
 
 
 
 
 
9
7
9
 
7
5
4
 
 
 
 
由於某兩行 (灰格) 上均出現了 「5」(黃字)，以致整個橫行上均不可能再有 「5」，所以紅色方格便一定是「5」了。推線法可用於大九宮格中同一直 (或橫) 行中其中兩格已出現一相同數字的情況，通常本人用於開始時。

 

記數法

到了推線法用盡之時，本人便會記下每一格的可能數值，當中也會有一些發現。

a
 
 
 
b
 
 
 
c

若圖中某一橫行中三格的可能數值詳列如下

格 a 、b 的可能數值同為 「1」、「3」；

而格 c 的可能數值則為 「1」、「3」、「8」：

那麼 格 c 一定是 8 了。而格 a 、b 則只會是 「1」或 「3」中任選其一。

 
a
 
 
 
 
 
 
c
 
           
b
    

若圖中某兩橫行中三格的可能數值均為「2」、「7」，那麼由於格 a 和格 b 沒直接關連性，故 格 a 和格 b 的數值是會相同的，而格 c 則是另一數值。

 

當然還有別的方法，此兩法僅供參考。望諸君得到數獨的樂趣。

 

參考文獻及網址：

Bammel, S. E. and Rothstein, J. "The Number of 9x9 Latin Squares." Disc. Math. 11, 93-95, 1975.

Garns, H. "Number Place." Dell Pencil Puzzles & Word Games. No. 16, May p. 6, 1979.

Royle, G. "Minimum Sudoku." http://www.csse.uwa.edu.au/~gordon/sudokumin.php.

Royle, G. "Sudoku Patterns." http://www.csse.uwa.edu.au/~gordon/sudokupat.php.

Weisstein, E. W. "Latin Square." From MathWorld. http://mathworld.wolfram.com/LatinSquare.html.

Weisstein, E. W. "Sudoku." From MathWorld. http://mathworld.wolfram.com/Sudoku.html.

 

Hosted by www.Geocities.ws

1