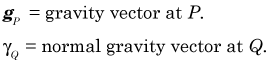
Then, the gravity anomaly vector is defined as:
![]()
The gravity anomaly, defined as a scalar quantitiy, is merely the difference in magnitude.

Definitions
In Heiskanen & Moritz's text, Physical Geodesy (pp.82-83), we find an intuitive description for gravity anomalies:
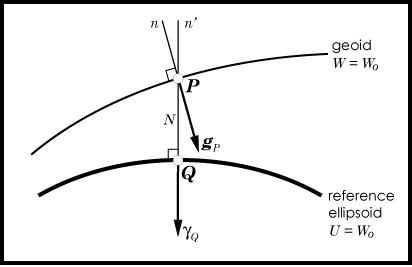
| Consider the following quantities (see figure at right):
Then, the gravity anomaly vector is defined as:
The gravity anomaly, defined as a scalar quantitiy, is merely the difference in magnitude. |
 |
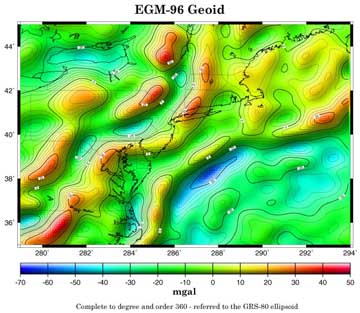
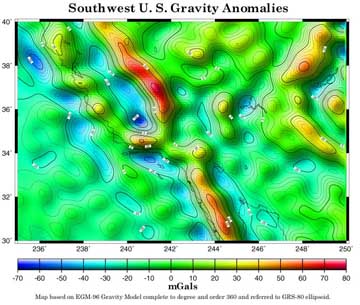
The figures below were generated on the basis of the EGM-96 gravity model complete to degree and order 360. What can be seen in these maps, when compared with those found on the geoid page, is that gravity anomalies are a higher frequency phenomena. In fact, geoid heights are related to gravity anomalies by Stokes' formula (p. 94 in Heiskanen & Moritz):
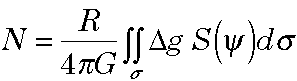
where R = mean radius of the planet; G = mean value of gravity; S(psi) = the Stokes's function which is a weighting function dependent on the spherical distance from the point of computation and the set of gravity anomalies for a given planet; and sigma = an integration over the whole surface of the planet. In other words, to determine a geoid height, one needs gravity anomalies distributed over an entire planet.
The inverse relationship is given by (Heiskanen & Moritz, p. 85):
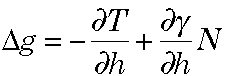
In this formula, we see that a gravity anomaly is given as a sum of the negative change in the disturbing potential taken with respect to height (the first term) and the product of the corresponding geoid height with the change in normal gravity taken with respect to height.
Last updated:October 8, 1999