This section in pdf form. triples1.pdf
If ![]() ,
, ![]() , and
, and ![]() are positive integers and
are positive integers and
![]() then the
solution
then the
solution ![]() is a Pythagorean triple. If
is a Pythagorean triple. If
![]() then
then ![]() is a primitive (or reduced) Pythagorean triple,
and the equation
is a primitive (or reduced) Pythagorean triple,
and the equation
![]() is a primitive Pythagorean
triangle.
Finding primitive Pythagorean
triangles with a given difference between the lengths of the
hypotenuse and a leg is a simple matter; from the parametrization
is a primitive Pythagorean
triangle.
Finding primitive Pythagorean
triangles with a given difference between the lengths of the
hypotenuse and a leg is a simple matter; from the parametrization
However, finding Pythagorean triangles with constant difference between the lengths of the two smaller legs leads to a Pell equation,
Hence, if one solution is found, other solutions can be found recursively. From which a closed form can be obtained.
The following scheme does not find solutions for every integer
![]() , only those where
, only those where
![]() , and not all of those. For
example, in the Pythagorean triangle
, and not all of those. For
example, in the Pythagorean triangle
![]() , there
exists no integer
, there
exists no integer ![]() such that
such that ![]() , and the scheme does
not generate the triangle
, and the scheme does
not generate the triangle
![]() where
where
![]() .
.
I'll use the alternative parametrization: ![]() is a primitive
Pythagorean triple if and only if there exists relatively prime,
odd positive integers
is a primitive
Pythagorean triple if and only if there exists relatively prime,
odd positive integers ![]() and
and ![]() ,
,
![]() , such that
, such that
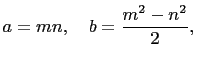 and
and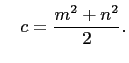
I'll give a closed form for ![]() and
and ![]() where
where
![]() . Let
. Let
where ![]() and
and ![]() are positive integers. Set
are positive integers. Set
![$\displaystyle =\frac{\left(1+\sqrt{2} \right)^{s-1}\left[2\left(1+\sqrt{2} \r...
...ht]+ \left(1-\sqrt{2}\right)^{s-1}\left[2\left(1-\sqrt{2} \right)+1\right]}{2}$](img207.gif) |
||
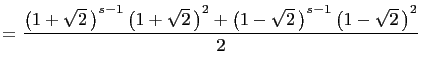 |
||
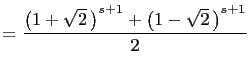 |
||
| (from (i) |
||||
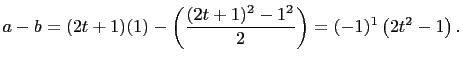
So the claim is true for
Assume it's true for ![]() . That is, assume
. That is, assume
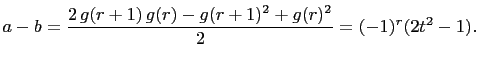
Then, for
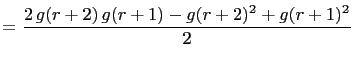 |
||
![$\displaystyle =\frac{g(r+2)[(2 g(r+1)-g(r+2)]+g(r+1)^2}{2}$](img241.gif) |
||
)+g(r+1)^2}{2}$](img242.gif) |
||
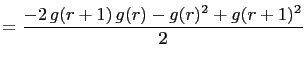 |
||
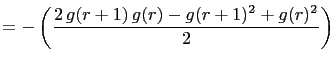 |
||
|
|