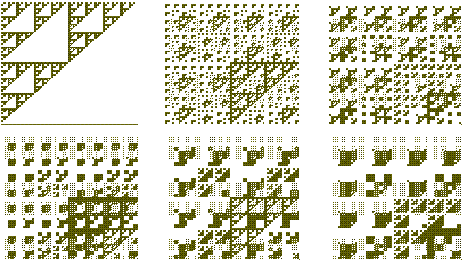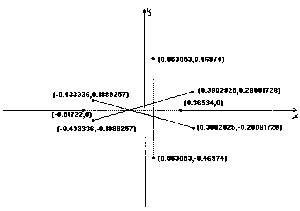Fractal report 44 Part 2
The Most Impressive Fractal J. A. Muth
Acceleration Man Malcolm Lichtenstein
Tent Inside Man Malcolm Lichtenstein
Some BAM Designs Malcolm Lichtenstein
Auto Correalation BAM Pattern Malcolm Lichtenstein
A Fractal in Visual Basic: Martin's Mappings John de Rivaz
Julia Set Compatible Perturbations Jules Vereschueren
General Power Mandelbrot Roger Bagula
The Most Impressive Fractal
by J. A. Muth <[email protected]>
When recursive formulas are calculated and displayed on the screen of a computer, intricate patterns
known as fractal images often appear. At first glance, these images appear to have no value beyond
decoration, but careful consideration reveals that the images are related to computers in a manner
remarkably similar to the way the objective world is related to its observers.
 To appreciate this relation we must remember that
fractal images and fractal formulas are two different
things. Fractal images are man made artifacts, which
can be coloured and manipulated as desired; fractal
formulas are fixed realities, which cannot be changed
without changing the image.
To appreciate this relation we must remember that
fractal images and fractal formulas are two different
things. Fractal images are man made artifacts, which
can be coloured and manipulated as desired; fractal
formulas are fixed realities, which cannot be changed
without changing the image.
Fractal formulas may be considered recipes -- mathematical recipes that can be prepared in many ways.
The Mandelbrot formula for example could just as easily be mapped to musical notes instead of a screen
and be made audible to our ears as an unending series of tones. This would be one way in which a blind
person might appreciate the world of fractals.
It is often stated that fractal images are infinitely detailed. This is true potentially, but in actuality it is not.
When a fractal image is examined closely enough, it breaks down into discrete units known as pixels.
These pixels are the limit to the fractal detail that may be obtained by examining the screen. If we want
more detail, we must recalculate the formula to a greater precision. Fractals are infinitely detailed because
the formula can be calculated to any degree of precision desired, not because the image on the screen has
infinite detail.
The situation with the objective physical world is similar. When an object of the physical world is
examined closely enough, it also breaks down -- first into molecules, then into atoms. And like the pixels
of a fractal image, these atoms represent the limit to the information that may be obtained by examining
the object with the senses. To go beyond atoms into the shadowy world of the quantum, indirect methods
and ultimately pure mathematics must be called upon. In this case the mathematics works only within the
quantum world; it makes no sense when applied to the everyday world around us. If a person were to
choose a single pixel of a typical fractal image, such as that of the Mandelbrot set, and ask what that pixel
is made out of, the answer would be, "the number of iterations required for that point of the Cartesian
plane, when iterated according to the formula Z(n+1)=Z(n)^2+C, to pass beyond a particular escape
radius." The pixel is a representation of the mathematical behaviour of that point, and nothing more. It is
not an object. It has no attributes until someone supplies them. To speculate about a physical pixel
existing in some dark closet would be meaningless.
The situation with the objective world is again similar. If a person were to ask what a particular "pixel" of
the real world, such as an electron, is made out of, the answer would be "1/2 unit of spin plus 1.6x10^-19
coulombs of negative charge plus 9.1x10^-28 grams of mass." Any attempt to picture an object that fits
this description would be meaningless. The electron is not a object which is simply too small to see; it is
its mathematical representation and nothing more. Just as with the pixel of the Mandelbrot set, it has no
attributes until someone supplies them by observing it.
 Physicists have long been trying to determine how
sub-atomic particles such as electrons, which unless
observed have no existence beyond their mathematical
descriptions, can constitute an objective world which
exists even when it is not being observed. Perhaps the
answer lies in the realm of fractals. Perhaps the
objective world of our senses is no more than a
manifestation in our minds of a fractal formula, just as a
fractal image is a manifestation on a computer screen of
a fractal formula. As bizarre as it seems, perhaps we are
mistaking the ephemeral images that flash across the screens of our minds for the unchanging reality
which lies in the underlying formulas alone.
Physicists have long been trying to determine how
sub-atomic particles such as electrons, which unless
observed have no existence beyond their mathematical
descriptions, can constitute an objective world which
exists even when it is not being observed. Perhaps the
answer lies in the realm of fractals. Perhaps the
objective world of our senses is no more than a
manifestation in our minds of a fractal formula, just as a
fractal image is a manifestation on a computer screen of
a fractal formula. As bizarre as it seems, perhaps we are
mistaking the ephemeral images that flash across the screens of our minds for the unchanging reality
which lies in the underlying formulas alone.
Calling upon common sense, one might dissent that the real world is obviously there whether or not its
image is actually present in the mind of an observer. The dissenter might point out that, on the outer
planets, our space probes have discovered the traces of past geologic events which took place without
observers being on the scene. But this dissention fails to settle the issue. If the comparison to fractals is
correct, the entire universe with all its events -- past, present and future -- is in reality a single, incredibly
complex fractal formula. The only thing that actually took place when we discovered the traces of past
events was that science found a way to display a previously inaccessible part of the formula.
It seems unlikely that these apparent similarities of the world of fractals to the objective world could all be
coincidental. Could the most impressive fractal image of all be the universe itself? Could we ourselves be
the living computers on which the fractal formula of the world is continuously being calculated and
animated? If the entire universe is a fractal image, we must be part of the image also. This possibility
raises an interesting question. If a way could be found to use fractals to determine the future with
certainty, and if a person saw himself killed in an accident, could that person avoid being at the scene, or
would an ineluctable force compel him to be there to meet his fate as scheduled?
One final thought: if the entire universe including its observers is in
reality an abstract fractal formula, who or what is the observer
transforming that formula into the tangible objects we call ourselves?
Acceleration Man
by Malcolm Lichtenstein
'Acceleration Man
'Escape criteria for accel is difference
'between two successive differences in
'orbits within inner Mandelbrot loop
screen 12
window (-2,-1.5)-(1,1.5)
for b=-1.5 to 3 step .006
d=d+1:c=0
for a=-2 to 1 step .0045
c=c+1
x=0:y=0:r=0
for k=1 to 15
l=r
x1=x*x-y*y+a
vel1x=x1-x
y1=2*x*y+b
vel1y=y1-y
x2=x1*x1-y1*y1+a
y2=2*x1*y1+b
vel2x=x2-x1
vel2y=y2-y1
accx=vel2x-vel1x
accy=vel2y-vel1y
r=SQR(accx*accx+accy*accy)
if r=>4 then exit for
if abs(l-r)<.001 then exit for
'resume at x2:y2-last of 3
'2nd-1st and 3rd-2nd used in acceleration calculation
x=x2:y=y2
next k
pset (a,b),k
next a
next b
Tent Inside Man
by Malcolm Lichtenstein
screen 12
for b=-3 to 3 step 6/480
d=d+1:c=0
for a=-3 to 3 step 6/640
c=c+1
r=1:k=0:x=0:y=0
while k<160 and r<4
k=k+1
l=r
xx=x*x-y*y+a
y=2*x*y+b
x=xx
u=abs(x)
v=abs(y)
'tent 0-5-0 for ABS x,y range 0 to 10
u=5-abs(5-u)
v=5-abs(5-v)
r=sqr(u*u+v*v)
if abs(l-r)<.001 then exit loop
wend
pset (c,d),k mod 16
next a
next b

Some Bam Designs
by Malcolm Lichtenstein
screen 12
s=1.45
window screen (0,0)-(640/s,480/s)
defdbl a,b
for b=1 to 128 step .5
for a=1 to 128 step .5
if (a and b)=0 then pset(a,b):'standard BAM - top left
pset(a+150,b),15*(((a and b) mod 3) mod 2):'top centre
pset(a+300,b),15*(((a and b) mod 5) mod 2):'top right
pset(a,b+140),15*(((a and b) mod 7) mod 2):'top centre
pset(a+150,b+140),15*(((a and b) mod 11) mod 2):'bottom centre
pset(a+300,b+140),15*(((a and b) mod 13) mod 2):'top centre
next a
next b
rem: program modified for PC by inserting the "15*" and the screen scaling lines and the step .5.
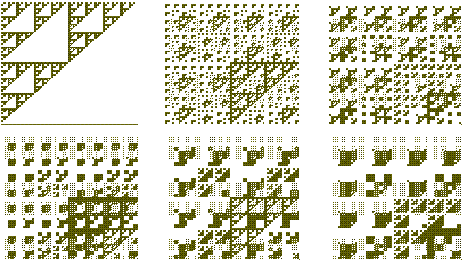
Auto Correalation BAM Pattern
by Malcolm Lichtenstein
Perhaps the method below could turn out to be of practical utility rather than just a recreational exercise...
It uses BAM as an auto-correalation pattern (on two cycles of a sine wave in this program). This could be
another method, in addition
to auto-correalation, Fourrier
analysis or image analysis
techniques, for observing
wave form component
patterns. As such there might
be circumstances in which it
could add to the usefulness
of other methods now
employed.
Therefore I am sending the
program and the graphic to
everyone in the hope than
any or all would see fit to
further pursue the matter,
mathematically (I have no
competence to do this
myself.)

screen 12
dim th(800)
pi=atn(1)*4
'two cycles of a sine wave 'recorded'
' and saved as an array for convenience
for aa=0 to 4*pi step 4*pi/800:'rem 800 for 400 lines on screen
a=a+1
th(a)=((SIN(aa)+1)*100):'scale *100 for BAM analysis
next aa
' auto-correalation BAM
' the first cycle is compared with
' itself, sucessively at angles
' differing by 0 to 2*pi
for angle=0 to 400: 'th(angle) range 0 to 2*pi
for a=1 to 400
if (th(a) and th(a+angle))=0 then pset(a,angle+1)
next a
next angle
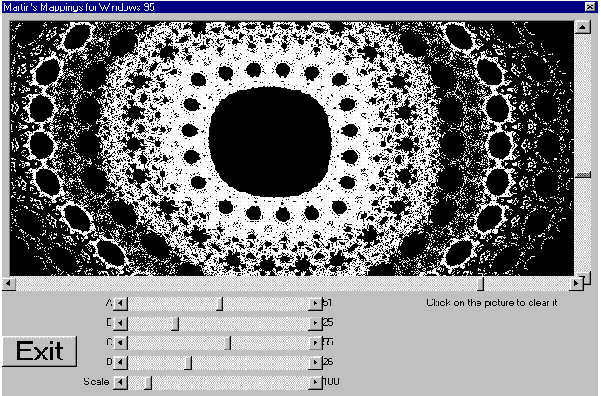
A Fractal in Visual Basic
Martin's Mappings
by John de Rivaz
This seems a fitting topic with which to include in the last issue of Fractal Report. Martin's Mappings
were the short program used in the issue -1, used as a promotional leaflet. Then it was only 13 lines in
GBBASIC, and you had to alter the code to alter the variables.
In Microsoft Visual Basic you have a lot more to enter, although it can be entered graphically. However,
once entered, you can alter the scale and change variables as the program is running. They key to this is
the insertion of "DoEvents" in the main loop. We may complain and mourn the loss of a simple
programming language, but you have to admit that Visual Basic and the languages that are to come will
offer far, far more.
I am appending the code and also a picture of the screen. I recommend that people set it up graphically
and then enter the code into command1. However this is not meant to be an all bells and whistles project,
just to show how "DoEvents" adds an additional dimension to fractal programming - modify the
parameters at the fractal grows.
VERSION 4.00
Click here to download a zip file containing the Visual Basic source code
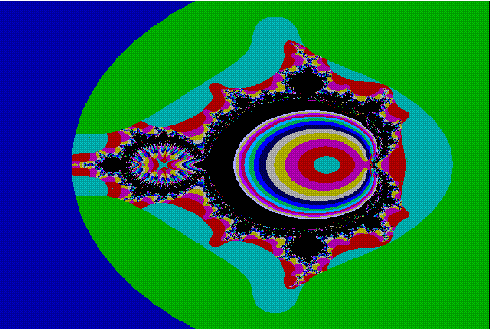
Julia Set Compatible Perturbations
- 3D set Application
by Jules Verschueren
Binnenstraat 53, B-3020 Veltem, Belgium
E-mail: [email protected]
Click here to download the files associated with this article
This article is a perturbation generalization to all Mandelbrot/Julia type fractal formulas with the idea that
this perturbation performed to a Mandelbrot type set also translates/transposes to the corresponding Julia
sets (eg. in contrast to the well known starting perturbation with z 0)
.
The original idea as well as the 3D type set with the formula:
Xn+1 = -axn - (1-a)xn2 - yn2 + cr
Yn+1 = 2xnyn + bzn + ci
Zn+1 = yn
are from an excellent article of M. Klein et al. in Computing & Graphics 1991; 15: 583-596.
The generalized perturbations can best be shown with the original Mandelbrot formula:
Xn+1 = xn2 - yn2 + cr + pr xn
Yn+1 = 2xnyn + ci + pi yn
The perturbations on the real and imaginary axes can be handled separately and some of the original
symmetries are preserved, at least for the Mandelbrot types. For the Julia type sets, the origin symmetry is
lost when either pr or pi <> 0.
Also, no matter how complicated the original formula, only 2 new additions and multiplications are
needed and the total execution time is thus not much prolonged.
As a real generalization in a program with different formulas, the perturbations can very easily be
implemented at the end of the normal calculations as follows (see also program at 'CalcZ:'):
IF RealPerturb = 0 THEN ZReal = NewZReal
ELSE ZReal = NewZReal + ZReal * RealPerturb
IF ImagPerturb <> 0 THEN ZImag = Zimag + ZImag *
ImagPerturb
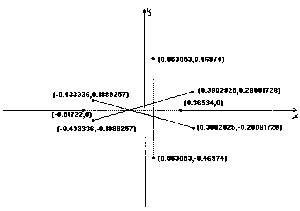 To show the vast, but consistent and gradual impact of
these perturbations, first an example from the original
Mandelbrot type set (Fig 1) with pr = -0.5, and a
corresponding Julia type set (Fig 2).
To show the vast, but consistent and gradual impact of
these perturbations, first an example from the original
Mandelbrot type set (Fig 1) with pr = -0.5, and a
corresponding Julia type set (Fig 2).
Fig1 (mandr-05):
Mandelbrot z2+c set with pr = -0.5
Fig2 (julr-05): Julia z2 +c set with pr = -0.5; (-0.0125, 0.639)

For a view of the
2-dimensional slices from the
3D Mandel type set I started
with a = b = 0 and then
varied a and b. A 'set' is only
obtained within some limits
of the parameters a (-3.2 <
NPar0 < 2.8) and b (-1.8 <
NPar < 1.85). For b = 0 and
a > 1.04 a 'floating island'
appears and the set is
opening up for a > 1.73.
Fig3: M sets with pr = pi = a
= b = 0
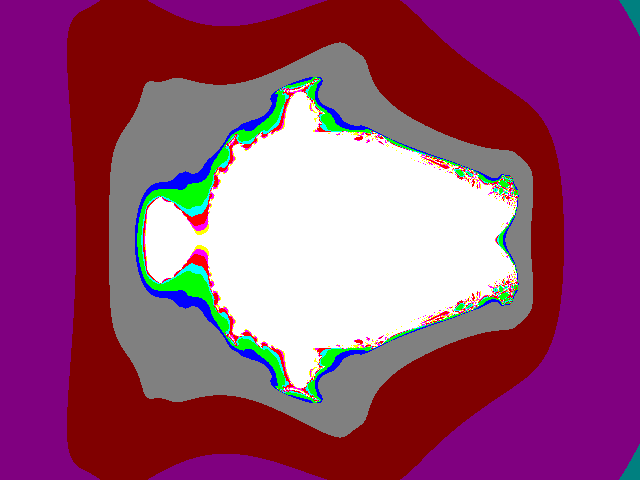
Fig4-16: As Fig3 but:
Fig4: a = -2;

Fig5: a = -1;
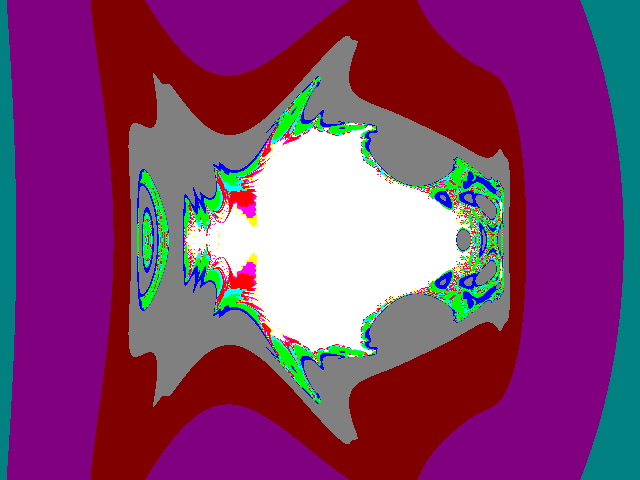
Fig6: a = 1.05;

Fig7: a = 1.73

Fig8: b = -1;

Fig9: b = 0.5
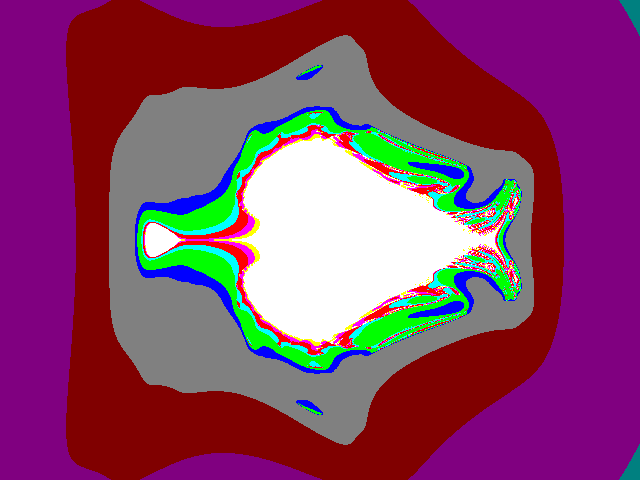
Fig10 = 1.5
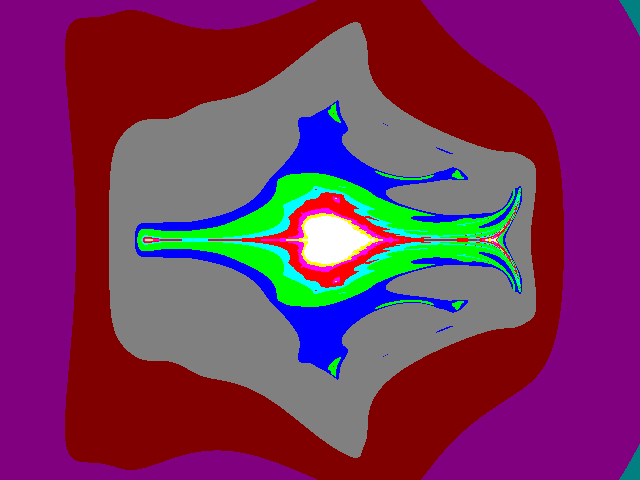
Fig11: pr = -1;

Fig12: pr = 0.5;
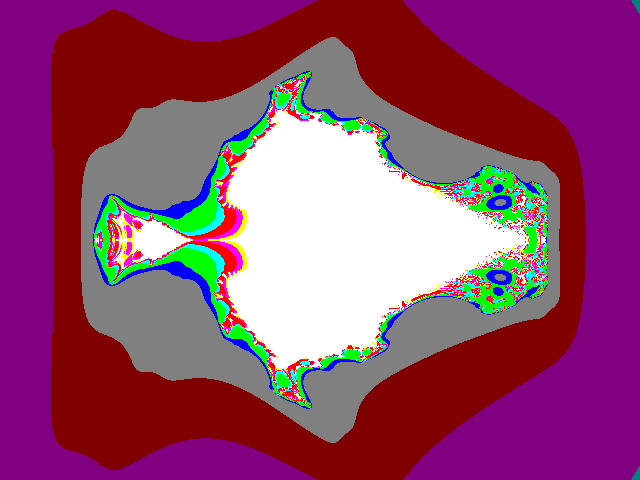
Fig13: pr = 1.4

Fig14: pi = -2.4;
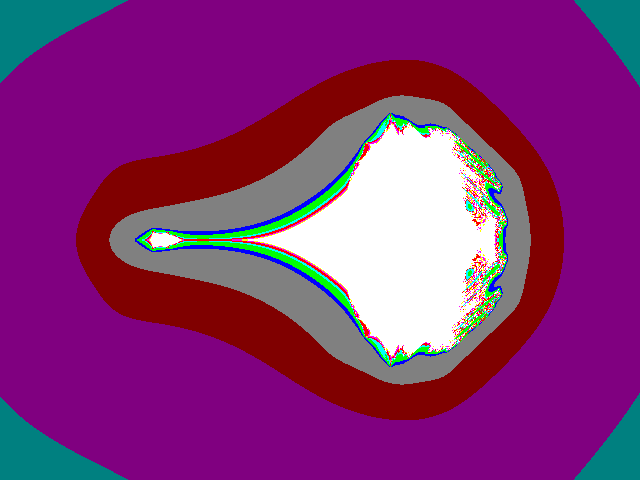
Fig15: pi = -0.3;
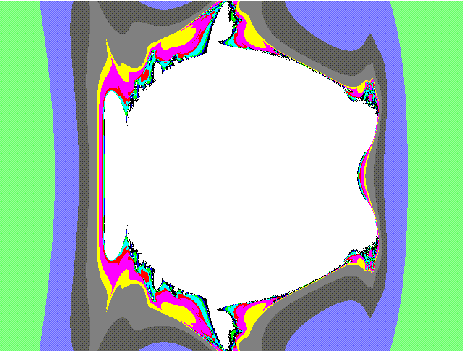
Fig16: pi = 1

For each of these settings you can then use different perturbations for pr and/or pi to create new sets ad
infinitum. From every single one you can obviously create a zillion different Julia sets...
Here again sets are only created within some limits for pr (-1.7 < ZRPerturb < 2.5), but there don't seem
to be limits for pi; sets are just progressively shrinking for larger values of pi.
Fig17-23: J sets with (r,i) coordinates and pr = pi = a = b = 0 except for:
Fig17: a = 1.73, (0.65,0);

Fig18: b = -0.5, (-0.336,0.855);
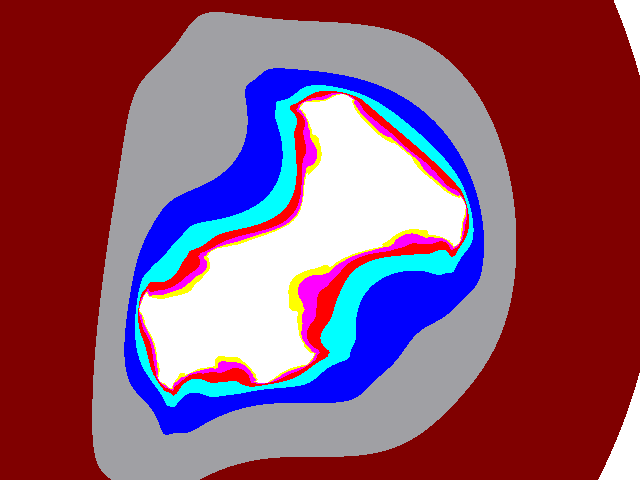
Fig19: pr = 1.4, (0.798,0);

For those who can experiment with FRACTINT, the perturbations can be obtained as follows (example
for the original Mandelbrot and Julia set):
MandPerturb (XAXIS) { ; z^2 + c + p3*z try p3(real) = 0.5 or -0.5
z=pixel: z=z*z + pixel + real(p3)*real(z)+imag(p3)*imag(z), |z| <
10 }
JuliaPerturb { ; z^2 + c + p3*z try p1 = (-0.0125,0.639)
z=pixel: z=z*z + p1 + real(p3)*real(z)+imag(p3)*imag(z), |z| < 10
}
REM "3D-MAND.BAS" (c) L.J. Verschueren, version 8 OCT 1996, QB + PB
compatible
REM Mandelbrot and Julia sets of type X = -a.x - (1-a).x^3 - y^2 +
c(r) [+ p(r).x]
' Y = 2.x.y + b.y + c(i) [+ p(i).y]
' Z = y
REM With perturbations along the real and imaginary axes,
transposing to Julia sets
REM Mandel type x-axis top/bottom symmetry is lost for p(i) <> 0
REM Julia type origin (0,0) symmetry is not present in this 3D model
' and is always lost for p(i) or p(r) <> 0
REM Variables and routines are same as in Fractal Reports 12, 15,
23, 29 and 36.
DEFINT I-K, M, O-P, S, X-Y: DEFDBL B-H, L, N, R, T, Z
start:
SCREEN 0: CLS : WIDTH 80: PRINT "Mandelbrot or Julia type set (M/J):
";
Ch$ = UCASE$(INPUT$(1)): IF Ch$ = "J" THEN Mandel = 0: PRINT "J":
ELSE Mandel = -1: PRINT "M"
PRINT "3-D or Classical (z) set (3/C): ";: Ch$ = UCASE$(INPUT$(1))
IF Ch$ = "C" THEN MandClass = -1: PRINT "C": ELSE MandClass = 0:
PRINT "3D"
PRINT "Grid coordinates (0 or Enter for defaults):" 'use 4/3 aspect
ratio
INPUT " Length, Height, LowX, LowY: ", Length, Height, LowX, LowY
IF Length = 0 THEN Length = 4: Height = 3: LowX = -2: LowY = -1.5
'defaults
IF NOT MandClass THEN
INPUT "Parameters a and b (-2.5 to 2.5): ", NPar0, NPar '3D
parameters a,b
END IF
'floating island at a>1.04, opening at a>1.73;
'sets only for -3.2<a<2.8, or -1.8<b<1.85
INPUT "Perturbation along Real/Imaginary axis (0 for default): ",
ZRPerturb, ZIPerturb
'sets only for -1.7<ZRPerturb<2.5
MaxIter = 99: Escape2 = 99: DifZ = .0001: DifZFAST = DifZ
ZReal0 = 0: ZImag0 = 0 'no starting
perturbation for Mandel
IF LowY * 2 = -Height THEN MirrorTB = -1 ELSE MirrorTB = 0 'assume
IF LowX * 2 = -Length THEN MirrorLR = -1 ELSE MirrorLR = 0
'symmetrical grid,
Sym = 0 'but no origin
symmetry
IF Mandel THEN 'Mandel type symmetry
and defaults
MaxCycle = 3: Iter1 = MaxIter \ 3: REDIM CycleZ(MaxCycle)
MirrorLR = 0 'no LR symmetry for these Mandel types
ELSE 'Julia symmetry and
defaults
MaxCycle = 0: Iter1 = 10
INPUT "Enter constant <CReal, CImag> : ", CReal0, CImag0
IF CReal0 <> 0 THEN MirrorLR = 0 'no Left/Right symmetry
END IF
IF CImag0 <> 0 THEN MirrorTB = 0 'no Top/Bottom
symmetry
Iter2 = 0: SetCol = 0: StartCol = 1: Kol1 = 15: MaxCol = 15: InType =
0
CorrCol = (MaxCol + 1) / LOG(Iter1 - Iter2) 'for logarithmic
color correction
Mode = 12 'VGA 16-color 640x480
SCREEN Mode: IF Mode = 7 THEN ScreenX = 319: ScreenY = 199 ELSE
ScreenX = 639
ScreenY = 479
DX = Length / ScreenX: DY = Height / ScreenY
IF MirrorTB THEN YEnd = ScreenY \ 2 ELSE YEnd = ScreenY
IF MirrorLR OR Sym THEN XEnd = ScreenX \ 2 ELSE XEnd = ScreenX
FOR Y = 0 TO YEnd 'main routine
LY = LowY + Y * DY
FOR X = 0 TO XEnd
LX = LowX + X * DX
GOSUB Iterate: GOSUB CalcColor
NEXT X: IF INKEY$ = CHR$(27) THEN Y = YEnd 'check Escape key
pressed
NEXT Y
Hold$ = INPUT$(1): IF Hold$ <> CHR$(27) THEN GOTO start
END 'end of main program
TestCycle: 'periodicity check
IF MaxCycle > 0 THEN
FOR I = 0 TO MaxCycle - 1
IF ABS(Z2 - CycleZ(I)) <= DifZ THEN Iter = Iter + MaxIter: RETURN
NEXT I
CycleZ(Iter MOD MaxCycle) = Z2
END IF
IF ABS(Z2Prev - Z2) < DifZFAST THEN Iter = Iter + MaxIter 'FAST
checking
RETURN 'TestCycle
CalcZ: 'update z and # of
iterations
IF ZRPerturb = 0 THEN ZReal = NewZReal ELSE ZReal = NewZReal +
ZRPerturb * ZReal
IF ZIPerturb <> 0 THEN ZImag = ZImag + ZIPerturb * ZImag
Z2Real = ZReal * ZReal: Z2Imag = ZImag * ZImag: Z2 = Z2Real +
Z2Imag
Iter = Iter + 1: IF CheckDifZ THEN GOSUB TestCycle
RETURN
Mandel2:
WHILE Iter < MaxIter AND Z2 < Escape2
NewZReal = Z2Real - Z2Imag + CReal
ZImag = (ZReal+ZReal)*ZImag + CImag
GOSUB CalcZ
WEND
RETURN 'Mandel2
Mandel3D:
Z = 0
WHILE Iter < MaxIter AND Z2 < Escape2
NewZReal = -NPar0*ZReal - (1-NPar0)*Z2Real*ZReal - Z2Imag + CReal
NewZImag = (ZReal+ZReal)*ZImag + NPar*Z + CImag
Z = ZImag: ZImag = NewZImag
GOSUB CalcZ
WEND
RETURN 'Mandel3D
Iterate:
IF Mandel THEN 'start Mandelbrot
point
ZReal = ZReal0: ZImag = ZImag0: CReal = LX: CImag = LY
ELSE 'start Julia point
ZReal = LX: ZImag = LY: CReal = CReal0: CImag = CImag0
END IF
Z2Real = ZReal * ZReal: Z2Imag = ZImag * ZImag: Z2 = Z2Real +
Z2Imag
'initial variables
IF Iter > MaxIter THEN CheckDifZ = -1 ELSE CheckDifZ = 0
'periodicity check on/off
Iter = 0
IF MandClass THEN GOSUB Mandel2 ELSE GOSUB Mandel3D 'start the
iteration
RETURN 'Iterate
CalcColor: 'determine color of
pixel
IF Iter >= MaxIter THEN 'point belongs to the
set
Z2Prev = Z2 'keep final Z2 for
FAST
IF InType = 0 THEN Kolor = SetCol ELSE Kolor = Iter MOD MaxCol +
StartCol
ELSEIF Iter > Iter1 THEN
Kolor = Kol1 'color points outside
but close to set
ELSE
Kolor = INT(LOG(Iter - Iter2) * CorrCol) 'Logarithmic coloring
outside set
IF Kolor = 0 THEN Kolor = 15 'just for not printing too much
black
END IF
IF Kolor THEN 'only when
Kolor<>background
PSET (X, Y), Kolor 'place original pixel
IF MirrorTB THEN PSET (X, ScreenY - Y), Kolor 'symmetric to Real
(X) axis
IF Sym THEN PSET (ScreenX - X, ScreenY - Y), Kolor 'symmetric to
origin (0,0)
IF MirrorLR THEN PSET (ScreenX - X, Y), Kolor 'symmetric to
Imaginary (Y) axis
END IF
RETURN 'CalcColor
General Power Mandelbrot
By Roger Bagula
Rem with special initial conditions
Rem which gives strangely directional fractals
Rem by R.L.Bagula 13 Sept 1996 copy rights reserved
Screen Open 0,900,900,64,LORES
Screen Display 0,129,30,320,200
Print " Input file save name"
Input S$
Print "input s the power of Mandelbrot transform,noninteger>1"
Input S#
Rem palette
For X=3 To 15 Step 2 : Colour X,(X*256+X*16+X*0.8)/2 : Next X
Curs Off : Cls 0 : Flash Off
Locate 0,2 : Pen 15 : Paper 0
N#=900 : M#=900 : E#=Sqr(151) : E1#=E#/6
For I#=-E1# To E1# Step 2*E1#/(N#)
Inc D
For J#=-E1# To E1# Step 2*E1#/(M#+0.5)
Inc C
A#=I# : B#=J# : K=0 : D#=Sqr(A#^2+B#^2) : R#=D#
Repeat
Rem the atan(0/0) =pi/2 or
Rem INITIAL CONDITIONS X=Cos(s*PI/2)+A : Y=Sin(s*PI/2)+B
If K=0 Then F#=0 : G#=0 : R#=1
Inc K
L#=R#
X#=F#
Y#=G#
If X#=0 and Y#>0 Then W#=Pi#/2
If X#=0 and Y#<0 Then W#=-Pi#/2
If X#>0 and Y#>0 Then W#=Atan(Y#/X#)
If X#>0 and Y#<0 Then W#=Atan(Y#/X#)
If X#<0 and Y#>0 Then W#=Atan(Y#/X#)+Pi#
If X#<0 and Y#<0 Then W#=Atan(Y#/X#)-Pi#
If Y#=0 and X#>=0 Then W#=Pi#/2
If Y#=0 and X#<0 Then W#=-Pi#/2
F#=R#^(S#)*Cos(S#*W#)+A#
G#=R#^(S#)*Sin(S#*W#)+B#
R#=Sqr(F#*F#+G#*G#)
Until Abs(L#-R#)<10^-3 or K>Int(E#*E#) or R#>=E#
If R#/L#<=1 Then T#=-1 Else T#=1
KK=Int(E#*E#-T#*K)
Ink KK mod 64
Plot C,D
If C>M# Then C=0
Next J#
Next I#
Save Iff S$
End





If you want to read more of Mr Bagula's programs, then you need to subscribe to:

This costs $20 in the USA and $50 elsewhere.
Write to
Roger L. Bagula,
11759 Waterhill Road,
Lakeside,
CA 92040,
USA.
This page hosted by  Get your own Free Home Page
Get your own Free Home Page
 To appreciate this relation we must remember that
fractal images and fractal formulas are two different
things. Fractal images are man made artifacts, which
can be coloured and manipulated as desired; fractal
formulas are fixed realities, which cannot be changed
without changing the image.
To appreciate this relation we must remember that
fractal images and fractal formulas are two different
things. Fractal images are man made artifacts, which
can be coloured and manipulated as desired; fractal
formulas are fixed realities, which cannot be changed
without changing the image.  Physicists have long been trying to determine how
sub-atomic particles such as electrons, which unless
observed have no existence beyond their mathematical
descriptions, can constitute an objective world which
exists even when it is not being observed. Perhaps the
answer lies in the realm of fractals. Perhaps the
objective world of our senses is no more than a
manifestation in our minds of a fractal formula, just as a
fractal image is a manifestation on a computer screen of
a fractal formula. As bizarre as it seems, perhaps we are
mistaking the ephemeral images that flash across the screens of our minds for the unchanging reality
which lies in the underlying formulas alone.
Physicists have long been trying to determine how
sub-atomic particles such as electrons, which unless
observed have no existence beyond their mathematical
descriptions, can constitute an objective world which
exists even when it is not being observed. Perhaps the
answer lies in the realm of fractals. Perhaps the
objective world of our senses is no more than a
manifestation in our minds of a fractal formula, just as a
fractal image is a manifestation on a computer screen of
a fractal formula. As bizarre as it seems, perhaps we are
mistaking the ephemeral images that flash across the screens of our minds for the unchanging reality
which lies in the underlying formulas alone.