ISSN 0964-5640
Cos1.par Yvan Bozzonetti 3
Letters 4
The Mandelbrot Crop Formations Kobus Nieuwmeijer 7
Tree Maker Dolores García García 8
Complex Probability Beziers of Three Polynomials In Iteration Time Roger L. Bagula 9
Random And Pseudo-random Walks Roger L. Bagula 10
B.C.S. Superconductors, Renormalizationand Yang-lee Theory Roger L. Bagula 12
Exploring C3FBC4 Yvan Bozzonetti 14
Inflation Tilings Paul Gailiunas 16
Inverse Mapping for Newton's Method Paul Gailiunas 18
Web Mappings Paul Gailiunas 20
Fractal Report is published by Reeves Telecommunications Laboratories,
West Towan House, Porthtowan, Truro, Cornwall TR4 8AX, United Kingdom.
Volume 5 no 30 First published December 1993. ISSN 0964-5640.
The future of Fractal Report will be transformation, probably a gradual one at that. We will, of course, continue to accept articles on fractals and chaos, but other items will start appearing from now on. A new title is still being sought, of the form <something> Report.
The next volume should see the transformation in progress, and a relaunch press statement will be issued to the computer magazines when there are a suitable number of new-subject articles.
However the format of text and a listing will not be changed. Emphasis will be on getting ideas across in a useable format, and the best use of publisher's and authors' time will be used to get this effect. Therefore whilst all efforts possible will be maintained to ensure accuracy, undoubtedly some mental input will be required of readers in implementing the ideas given. This subject is expanded in replies given to letters in a large letters section in this issue.
Subscribers paying by bankers order are asked to produce new ones, cancelling their old ones. This has nothing to do with the changeover, more with the National Westminster Bank's policy towards small business accounts. Their charges were out of all proportion to the funds handled, and therefore we have changed to the Allied Trust Bank, who offer free banking to small business subject to certain constraints. Any readers running a small business and interested in this, please write to us and we will forward your name. (Customers get �25 for any new customer they introduce.) You will receive further details, without obligation, of course.
Also this year RTL lost its 'Ltd' due to audit costs, which even the accountant admitted were extortionate. He said that small companies have to undergo the same accounting tests as large ones, and the time taken has to be paid for. (This is hardly surprising when one considers that far more MPs, who make the laws, are accountants or solicitors or barristers than anything else.)
This year saw the start of Terra Libra, an organisation aimed at helping people to improve their freedom. An important part of their package is a resource sheet and Fractal Report and Longevity Report are listed therein. Already replies have been forthcoming from this source.
So far the results from Select Information Exchange have not been encouraging. Over 50 free samples have been sent out, but no subscription has resulted so far.
Nevertheless there are people out there who are still keen, and we do get orders for the complete set of back numbers. These orders go a long way to keep Fractal Report going, and it is amusing to note that the cost of posting the now heavy parcel overseas is very nearly as much as the original price for a single volume subscription!
Fractal Report is nothing without its contributors, and despite moans from some people about various inaccuracies, generally the articles are well received. I hope that the widening of the scope for articles will eventually lead to a new title with a strong fractal coverage and a renewed subscription list.
Fractal CD-ROM
Quanta Press announced on 9 September the release of Chaos: Fractals & Magic on Compact Disc-Read Only Memory (CD-ROM). This disc is immediately available in the ISO 9660 format for DOS and Windows PC platforms.
The formal release of Chaos: Fractals & Magic was made at the 3rd Annual Chaos Network Conference being held at the Landmark Center in downtown St. Paul (MN). Conference attenders were astonished with the disc and it's depth of coverage on the field.
The disc is a collaborative effort between Quanta Press and several leading organizations and individuals involved with chaos theory. These include Leonardo; the Journal of the International Society for the Arts. Sciences. and Technology: Bourbaki, Inc., a leading producer of fractal imagery and associated software; Mitchell & Mitchell, purveyors of world class nature photography and fractal images; and Jack Stein Grove, a world-renown marine biologist and photographer.
The disc includes an extensive annotated bibliography on chaos, a chaos magic section, poetry and prose, and expanded glossary, Leonardo theme packs of article reprints covering fractals, the arts, visual mathematics, and over 300 computer generated and naturally occurring fractal images.
Chaos, Fractals & Magic on CD-ROM is immediately available for sale in the DOS and Windows format. The suggested retail price for the disc is $69.95 (plus
shipping). For more information on Chaos: Fractals & Magic or any Quanta Press CD-ROM title, please feel free to contact: Dennis E. Burke Director of Marketing Quanta Press, Incorporated 1313 Fifth Street SE, Suite 223A Minneapolis MN 55414 (USA), (612) 379-3956 telephone, (612)623-4570 facsimile.
The company also produces FracTools III which is an integrated graphics system for generating, modifying and printing an infinite number of fractals or other images. The CD-ROM contains 590 .PCX images in 141 megabytes for slide shows, screen savers, and kaleidoscopes. The program also supports other graphics formats, and a range of video modes from EGA to VESA and S3.
Fractal Translight Continues
Robert Bagula's fractal newsletter dated December has been mailed to his patrons who have donated at least $20 (USA) or $90 (elsewhere.) He has sent for review four pages, one of which is the "any comments" questionnaire that appeared in the last issue.
The front page consisted of artwork, produced by a computer program that distorts images etc. I though the two pictures were very effective. One of the articles was about folding space and spacetime, with various equations and a picture. I am not sure whether the picture relates to the text.
The other article was a program and a picture entitled Comparator neuron Partial Simulation. I was unable to evaluate whether the title relates to the picture and program - there was no other text. Again the picture was excellent and if I get time I may try and type the program in, but as it was rather badly photocopied and reduced this could be difficult.
Again I would say that there is some interesting ideas, art and work here, and but I do think that Mr Bagula would benefit from some guidance and help with the actual publication. I gather from his letters that many people operating other newsletters and business relating to fractals and chaos have given up on him, which may be a pity.
Since the above was written, we have received further issues, dated January, February and March 1994.
The January issue included a "design a space ship" challenge. It should be buildable using present technology and could be assembled in orbit using the space shuttle. Also there were reviews of other newsletters and comments about their editors. Fractal Report was well received. The Yang-Lee article in this issue of Fractal Report is preprinted from this issue of Fractal Translight Newsletter and there are many more like it there.
The February issue's editorial will be on crime and morality, but the theme doesn't appear to be extended into the programs, except for the story The Stainless Steel Vulture.
March's issue will contain another short story Pooperman and the editorial is on forgiving, expressed in poetry. There will be the usual mix of maths, programs and pictures, and one article on Dimensional Iteration in the Mandelbrot Set will contain further comment on the reception of Mr Bagula's ideas by others involved in fractals.
If you have an Amiga you can type these programs in as they come, otherwise conversion, as with most BASICs, is easy. I have suggested to Mr Bagula that he may like to produce a disk for Amiga owners, but of course a lot of time is needed for disk duplication.
Fractal Translight Newsletter for 1994 is offered for a donation of $20 US/$90 foreign. Uncompromising "Outlaw Science" and art, stories ... music of the next century here today! Publisher: R.L. Bagula, 11759 Waterhill Road Lakeside California 929040 USA.
Video Compression Process
to Offer films on Demand
Down telephone Lines
If it was 1 April maybe I wouldn't believe it, but an article in The Financial Times dated 30 September says that BT is considering offering a service whereby people can dial up a film and have it sent to them down the telephone lines. It would be reproduced with similar quality to the average video recording. In addition, an ordinary 'phone call will break into the film so the line won't be tied up.
The compression technology that compresses the audio and video down to the telephone bandwidth is most likely to be fractal in nature, although the article only dealt with the financial and business aspects of the service.
Considering that the average phone line is unused most of the time this seems to be an excellent idea. Given that the cost will not be the same as with an ordinary phone call (otherwise it would not compete with ordinary video libraries), this would be a real alternative to illegal home taping to build up personal libraries of films. Assuming that most people watch a film they have copied only very infrequently it would probably be cheaper to rent via the telephone each time rather than keep a copy.
Integral Errors
Dr M. Ecker wrote in to point out errors in the integral formulae in Yvan Bozzonetti's article on page 7 of Fractal report 28.
The integral of x3 is x4/4 plus a constant, not as stated. This is more of a hash up with the layout than any misunderstanding of the principles, and the rest of the article is not affected.
by Yvan Bozzonetti
sample1 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C1F3
corners=-1.36441165/-1.29041713/0.136356115/0.191829979 inside=0
}
sample2 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C1F3
corners=-1.32729834/-1.32094312/0.147002339/0.151770294 inside=0
}
sample3 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1F3
corners=-2.178272/1.821711/-1.499985/1.5 inside=0 logmap=yes
}
sample4 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FA3
corners=-1.732592/2.267392/-1.499985/1.5 params=1 inside=0
logmap=yes
}
sample5 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FAB3
corners=-2/1.999984/-1.499985/1.5 params=1/0/0.5/0.20000000000000001
inside=0 logmap=yes
}
sample6 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FAB3
corners=0.83592147/1.0359078/0.00018668175/0.15016311
params=1/0/0.5/0.20000000000000001 inside=0 logmap=yes
}
sample7 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FABC3
corners=-2/1.999984/-1.499985/1.5 params=2/1/0.5/0.5
}
sample8 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FABC3
corners=-2/1.999984/-0.07828045/2.921705 params=2/1/0.5/0.5
}
sample9 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FABC3
corners=-2/1.999984/-1.499985/1.5 params=3/5/0.5/0.5 inside=0
}
sample10 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FABC3
corners=-2/1.999984/-1.499985/1.5
params=2.5/3.2000000000000002/0.5/0.10000000000000001 inside=0
}
sample11 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FAC3
corners=-2/1.999984/-1.499985/1.5 params=2.5/0/0.5/0.5 inside=0
}
sample12 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FB3
corners=-2/1.999984/-1.499985/1.5 params=2.5/0/0.5/0.5 inside=0
}
sample13 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FBC3
corners=-2.735373/1.264611/-1.73798/1.262005 params=2.5/0/0.5/0.5
inside=0
}
sample14 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C1FC3
corners=-2/1.999984/-1.499985/1.5
}
sample15 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C2F3
corners=-2.887321/2.887289/-2.165438/2.165492 inside=0 logmap=yes
}
sample16 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FA4
corners=-2.089136/1.910847/-2.001027/0.9989586 params=0.5/1 inside=0
logmap=yes
}
Sample17 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FB4
corners=-2.089136/1.910847/-2.001027/0.9989586 params=0.5/1 inside=0
logmap=yes
}
sample18 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FCDB4
corners=-2/1.999984/-1.80061/1.199375 params=-4.5/0/5.5/-3 inside=0
}
sample19 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FD4
corners=-2/1.999984/-1.975975/1.024011 params=0/1 inside=0
logmap=yes
}
sample20 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FD4
corners=-2/1.999984/-1.499985/1.5 params=-0.75/0.5 inside=0
}
sample21 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FA3
corners=-2/2.000005/-1.500014/1.5 params=3/0.20000000000000001
inside=0
}
sample22 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FAB3
corners=-2/2.000005/-1.500014/1.5 params=3/0/2.5 inside=0
}
sample23 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FABC3
corners=-2/2.000005/-1.500014/1.5 params=2/1/0.5 inside=0
}
sample24 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FAC3
corners=-2/2.000005/-2.276636/0.7233784
params=3/0/0.20000000000000001/0.10000000000000001 inside=0
}
sample25 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FB3
corners=-2/2.000005/-1.500014/1.5 params=3/0/0.5 inside=0
}
sample26 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FBC3
corners=-2/2.000005/-1.500014/1.5 params=3/0.5/0.5 inside=0
}
sample27 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FC3
corners=-2/2.000005/-1.500014/1.5 inside=0
}
sample28 { ; worth to look at and zoom in
reset=1600 type=formula formulafile=fractint.frm formulaname=C2FC3
corners=1.1924831/1.3924908/0.15045917/0.30046415 inside=0
}
sample29 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FA4
corners=-2/2.000005/-1.500014/1.5 params=1 inside=0
}
sample30 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FAB4
corners=-2/2.000005/-1.500014/1.5 params=1/0/5 inside=0
}
sample31 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FABC4
corners=-2/2.000005/-1.500014/1.5 params=1/4/0.5 inside=0
}
sample32 { ; exploding star
reset=1600 type=formula formulafile=fractint.frm
formulaname=C3FABCD4 corners=-2/2.000005/-1.500014/1.5
params=1/3/2/0.5 inside=0
}
sample33 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FABD4
corners=-2/2.000005/-1.500014/1.5
params=1/2.5/0.5/0.10000000000000001 inside=0
}
sample34 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FAC4
corners=-3.035194/2.485936/-2.070444/2.070424 params=1/0/6 inside=0
}
sample35 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FACB4
corners=-2/2.000005/-1.500014/1.5 params=1/3/2/2 inside=0
}
sample36 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FACD4
corners=-2/2.000005/-1.500014/1.5 params=1/2/0.5/0.5 inside=0
}
sample37 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FAD4
corners=-2/2.000005/-1.500014/1.5 params=1/0/-0.5/0.5 inside=0
}
sample38 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FAD4
corners=-3.058497/0.9415078/-2.959311/0.040703 params=1/0/-0.5/0.5
inside=0
}
sample39 {
reset=1600 type=formula formulafile=fractint.frm formulaname=C3FADB4
corners=-2.289694/1.710311/-1.500014/1.5 params=1/0.5/2/2 inside=0
}
sample40 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FADC4
corners=-2/1.999984/-1.499985/1.5 params=1/0.5/5 inside=0
}
sample41 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FB4
corners=-2/1.999984/-1.975975/1.024011 params=1/0.5/5 inside=0
}
sample42 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBC4
corners=-2/1.999984/-1.499985/1.5 params=2.5/0.5/5 inside=0
}
sample43 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBCA4
corners=-2/1.999984/-1.499985/1.5 params=2.5/3/1/1 inside=0}
Sample44 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBCD4
corners=-2/1.999984/-1.499985/1.5
params=4/7/0.10000000000000001/0.20000000000000001 inside=0
}
sample45 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBDA4
corners=-2/1.999984/-1.499985/1.5 params=-5/0.29999999999999999/1
inside=0
}
sample46 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBDA4
corners=-2.02244145/-1.9664427/0.195977271/0.23797524
params=-5/0.29999999999999999/1 inside=0
}
sample47 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBDC4
corners=-2/1.999984/-1.499985/1.5 params=1/0/6/3 inside=0
}
sample48 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FCD4
corners=-2/1.999984/-1.499985/1.5 params=-3/2/0.69999999999999996/-1
inside=0
}
sample49 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FCDA4
corners=-2/1.999984/-1.099124/1.900833 params=-4.5/0/0/-1 inside=0
}
sample50 {
reset=1513 type=formula formulafile=fractint.frm formulaname=C3FBD4
corners=-2/1.999984/-1.499985/1.5
params=9/0/0.10000000000000001/0.10000000000000001 inside=0
}
Editorial note: This file has had the colours removed as they would be impossible to type in. A disk is available from us with this file (with colours), the previously published .FRM files, and some GIFs, for �5 copying fee, please state 1.2M or 1.4M. See also the article by Yvan Bozzonetti in this issue.
From Mr Jon Horner
Mainly my comments the illustrations and program listings in Fractal Report, plus one or two other observations regarding the newsletter.
Regarding the illustrations I would like to suggest that:
1 ALL illustrations carry a text label which identifies the authoring program, the co-ord data, the formula, and (less important) the author.
2 You only use illustrations for which the authoring program is available to your subscribers.
The reasons for my suggestions are that I believe many people would want to recreate the illustrations for themselves, and then be able to further explore the program which created them. Showing illustrations that the reader cannot recreate is potentially very frustrating.
Instances where I believe this would have been helpful are:
the Amiga Gallery in FR 28.
the Epsilon Cross illus from Warut Roonguthai FR 28.
the cover of FR 27.
FR 25, p15.
FR 25, p13. The text of the accompanying article states "The presented figure shows the behaviour of the Newton method used to solve z^3 - 1 = 0." but the code in the article is for the Julia set on the M-set. I doubt many of your readers will be able to make the adjustments to the code which are necessary to produce the illustration.
FR 24, p5. This was an extremely frustrating example of giving most of the ingredients (program and formula) but no co-ords!
FR 22, p8.
FR 22, cover.
There are others but these will serve to illustrate my points.
My questions regarding the program code are:
1 Is the code printed from:
a) magnetic data provided by the author?
b) reproduction of hard copy provided by the author?
c) transcription from hard copy provided by the author?
I ask because several items have contained errors which prevent the code working as intended - e.g.:
FR 23, p5. - 6 lines up from bottom of page FUNCTION reInv ((u()) should read FUNCTION reInv (u())
- The Module containing procedures for calculating with complex variables appears to have been duplicated.
- In this same module DECLARE FUNCTION reInv (u(), v()) and DECLARE FUNCTION imInv (u(), v()) should not have the `v())'
- Quick Basic 4.5 won't accept the code as printed.
FR 15, p12. - The routine calccolor contains the variable MaxColor. This is the only instance of MaxColor in the entire program, and suggests it is a typo for MaxCol, also used in this routine and elsewhere.
- I'm also suspicious about Kolor and Color, but as I haven't been able to get this program working fully yet, I'm not sure!
FR 14, p15. - Line 270 for scr_wdth read scr_width
FR 6, p11. - Line 6 - CONST yellow s/b CONST yellow% Line 7 - CONST cyan s/b CONST cyan%
I haven't transcribed ALL the FR code, but this sample would indicate the probability that there are other errors. What I find strange is that I cannot recall ever seeing feedback from the author or other readers regarding these errors. Does this mean that no-one is using the code or is that old enemy inertia at work again?
One of my reasons for raising the code question is that I am collecting all kinds of code from books and Fractal Report, ON DISK, and working! Most of it has been sent to FRAC'Cetera from subscribers whom we share. Some way or other I propose making it available to my readers, and am also quite happy to offer it to yours. My hang-up here is that it could undermine one of your own strongest features. Despite this I can't help feeling that we all would benefit if the code you publish was also available on disk and working - no transcribing and debugging for the reader (most of whom as our mail bags attest, have far too many calls on their time already).
Please let me know your thoughts on this proposal.
This leads me on to :-
Who owns the copyright on articles and code published in FR? There does not appear to be any copyright notice printed in the newsletter, which suggests that authors retain the copyright. My main reason for asking is because I would like to make greater use of the code by publishing some of it in FRAC'Cetera, and also include some of it in the BASIFRAG project. In case you haven't delved that deep into FRAC'Cetera, BASIFRAG is our fractal generator project. Some routines previously published in FR have already been or are pending inclusion, some submitted by their original authors, but more often submitted by third parties who have rewritten the code in Quick Basic or QBasic.
Have you ever considered conducting a survey of your subscribers, say at renewal time, to establish what equipment they have, and for the program enthusiasts, what languages they use? I ask this because I know that your subscribers, unlike my own, are not all PC based. This means, for instance, that the non-PC based readers will get little benefit from the Fractint material that forms a growing part of FR's content. Equally, those using other platforms have little material aimed specifically at them - witness the letter from John Reece in FR 28 (though in his case, as an Amiga user, he has recourse to Cade Roux's Amiga Fractal Exchange).
One has to ask - does this matter? - how many Amiga subscribers do you have? - if they form just a tiny minority, is it worth publishing Amiga specific material which 98% of the readership will find useless?
It just seemed to me that you might learn something from a detailed profile of your audience, that you could put to use when shaping future FR's.
Fractal Shopper, on the face of it, seems like a great idea. However, I suspect it is not as attractive in reality as it looks on paper. It is significant that Fractal Report has only 100-150 subscribers, yet is itself being promoted to 2000 contacts through Fractal Shopper. FRAC'Cetera also had the benefit of a mailer inclusion with a major publishers' newsletter. The mail list was 200+ - we received THREE enquiries (NB - enquiries NOT subscriptions!). Theoretically your 2000 contacts each have some interest in fractals - if this is so, why don't more of them subscribe to FR?
On balance, I feel Fractal Shopper will probably not produce sufficient results to warrant the cost of the ad. I wish I could be more supportive, but the economics seem too unfavourable.
Jon Horner, Editor FracCetera Le Mont Ardaine Rue des Ardaines St. Peters Guernsey GY7 9EU C.I. Tel: 0481 63689. CIS: 100112,1700
Editorial Comment
The answer to your question re the program code really answers every single point, at least as far as the publisher is concerned. All material is sent either on disk or as camera ready copy. Sometimes I add figures to make the newsletter look better, and time related pressure could cause caption errors, as have been pointed out in the past. Pressures on my time and alternative opportunities in desk top publishing mean that if Fractal Report is to continue authors have to be relied upon to send accurate easy to use work.
I would also point out that authors are very poorly paid (in the form of free issues) for the time that they spend on their Fractal Report articles, and readers should be grateful for what they have provided, rather than berating them for typos and other errors. One should remember that commercially computer programmers are very highly paid people and if the programs in Fractal Report were paid for at commercial rates spread out over the readership subscriptions would probably cost hundreds if not thousands of pounds. Even then, commercial programmes have errors, such as WordPerfect 6.0 which is then reissued as "maintenance upgrades" to correct them.
So really the authors are contributing editors, and of course they retain copyright. Sometimes they have a little time to correspond on their work, and include an address, and those with lots of free time even give telephone numbers.
Fractal Report has never received enough material to be that selective, although I must say that most articles have some merit, even if they do contain the inaccuracies that Mr Horner has discovered.
Even if we have only a few Amiga and Atari subscribers, their articles don't seem to attract complaint. PC based readers have Fractint. (Amiga readers have plenty this time with Roger Bagula's contributions).
There could be a case for someone producing a fast Fractint formula compiler for the 68000 machines with input and graphics drivers for the Mac, Amiga and Atari. I should think it would be best if written in assembler, and it would be a job to be tackled by someone who has written a version of the C language. Failing that someone could probably write it in C, or indeed if Fractint is in C the code from that could be adapted. I believe that the source for Fractint is also in the public domain for anyone who would like to try.
With regards to the first three numbered points, yes this would be very nice, but very time demanding of both myself and our contributors, as said earlier in this comment. Writing and perfecting articles is not a quick and easy job, and considering how badly paid Fractal Report articles are (merely a free sub to the following volume) I think that we should be grateful to those who do contribute them. The complaints probably also explain why so little detail is given in fractal articles in professional books and journals - no one can tick off the author for not getting some detail right.
If we had a circulation of a couple of thousand we could probably afford to pay someone to check every submission carefully. But whether we would be a magazine for enthusiasts writing for other enthusiasts I would somehow doubt.
Fractal Shopper
The problem is really with all advertising. It is too expensive unless you are a multinational or (locally) a new car sales outlet or estate agent. That is to say these relatively wealthy organisations set the costs in a field where market forces are the only forces. There are no raw materials (except in direct mailing).
Fractal Shopper aims to break even with costs of printing and mailing approx 2,000 people and possibly providing a subsidy for Fractal Report. The latter aim was never achieved, and at the time of writing Fractal Shopper looks very sick and checks and cheques may have to be returned. This is a pity as some prestigious organisations were interested.
The future of Fractal Report
This depends on whether people still want it in sufficient numbers to continue sending in material and paying for subscriptions.
One possibility is to reduce the subscription and format for those few who want it, ie break any pretence of a magazine and send photocopied sheets. Personally I think there are too many subscribers to make this practicable at present and it would be a pity as articles are more likely lost in this format.
Another might be to sell the back numbers at cost with the mailing list to someone interested in taking it over and putting new ideas into it.
And, of course, the whole thing could fizzle out, although if it dies with me I will ensure that the full six issue volume is finished. The future does not look good with several fractal enterprises closing and specialist computer magazines ending. Modern PCs seem less easy to program and modern "applications" seem beyond the average person to compete with. Vast amounts of RAM and disk memory put the programmer further and further away from the CPU, cut off by operating systems and graphics interfaces that slow systems up despite their advantages for the users of programs. How can you poke screen pixels into the latest super windows accelerator card with gigabytes of RAM as you could with old Z80 machines? You have to send numbers via vast interface programs that come with the card. In practise you probably have fun messing about with Fractint instead.
(See also the editorial in this issue for future plans.)
From Mr John Topham
I have been working on a simple computer model of a gravitational lens. There are several intriguing types. I could write an article for the new newsletter explaining what they are, how I went about modelling them and include a simple BASIC program for people to experiment with.
Response:
This is just the sort of thing we are looking for, and it is encouraging to note that the first suggestion received is something I had not thought of or mentioned in the list of possible ideas.
From Mr Bev Mason
I agree with the suggestions that Fractal Report should have more diverse subject matter. Most of the material I find hard going, possibly because it has the minimum of explanation. Obviously in such a small publication you cannot indulge in lengthy simple language explanations. To do so would in any case probably bore your more erudite readers to the stage where you would lose them. However there must be many like myself who use their computers for pleasure only, and who do not enjoy the hard work of interpreting Fractal Report in its present form. I must confess that for a long time I have done little more than read the editorial, announcements, and readers' letters, and, after a very quick glance at the subject matter, put it in the file.
While I would not suggest dropping or changing the fractal content I think if such material were to be interspersed with subjects such as those suggested the Report would appeal to a much wider readership. (How about Fracto-Graphics report?)
I am interested in producing pictures from fractals, eg Mt Mandel type, enhanced using ray-tracing techniques. I would suggest therefore that ray tracing, using fractal inputs, would be a suitable subject.
I find that Fractint will not print pictures from my PC using my 9-pin Shinwa printer. I should very much like to see a BASIC program for printing GIF images from a file, or images from the screen, in which the codes sent to the printer could be adjusted. Presumably it would also need to be adjusted for different screen modes. I had such a program for my Amstrad CPC, which printed in black, white, and two shades of grey, but I have lost it.
Comment:
If it can be done simply, BASIC listing of how to decode all the various graphics formats into a form that can be manipulated by BASIC would seem a worthwhile project. This could then form the basis of further articles on subjects such as morphing.
A program to print the screen written in BASIC may be very slow running. Has anyone else got a Shinwa printer and got it to print from Fractint?
From Mr Gerald England
Thanks for the recent copies of Fractal Report and Longevity Report and for mentioning NHI Review therein.
Regarding the latter, I try sending issues to different reviewers, hopefully the more open-minded ones. Their scepticism is probably no more than an adequate reflection of the general public's apathy to all alternative ideas.
I think for some of us Fractals are indeed no more than pretty pictures. My wife asked me to define the word for her recently and I couldn't. Nor was the word to be found in an otherwise very up-to-date dictionary. I therefore welcome your idea of expanding the scope of the magazine. To that end I enclose a short article Poetry & Computers. It is based on part of an article that appeared in Dial 174 whose editor had asked me to write about various aspects of my work. I have amended to it some useful address. After the appearance of the original article I heard from a writer who is using the program to generate prose.
PS I typed in the short Popcorn program for a recent Fractal Report - had to change a line or two to suit GWBasic, but it creates a nice screen display.
Comment
The article is one of the type that have been suggested for the new newsletter. It describes the use of some shareware that is available to assist people composing poems.
The Mandelbrot Crop Formations
by Kobus Nieuwmeijer
Three Mandelbrot formations have appeared so far.
1. The first on the night of 11th/12th August 1991 in a wheat field owned by Mr. Hugh Raybone of Ickleton Grange Farm, near Duxford in Cambridgeshire, the formation was observed by the farmer. The formation was surveyed by the Centre of Crop Circle Studies the following Friday.
The media got hold of the news by the weekend, and the crop was harvested by Wednesday. The formation came as a surprise to most because of it's form, recognised to be almost a perfect copy of the Mandelbrot Set. Suspicion of a hoax also grew because it appeared in the County associated with Professor Mandelbrot's calculations (Mathematics Department of Cambridge University). The central tramline is exactly incident upon the corner post of a small wedge shaped wood standing in the middle of the field. The tramline continues downhill and ends within ten metres of the farmhouse bedroom window. This places the hill formation 600 meters away and in direct view of the farm house. Furthermore, a frequently used road is only 100 metres away. Remembering it formed in season at night and measured some fifty by sixty metres, the local farmers found it inconceivable that it could have been a hoax. It would have needed floodlights to achieve it's exactness. There were no sign of footmarks following the sweeping pattern nor any sign of marks left by machinery to create this effect.
The formation
The formation was located at the summit of a gentle rise (100m altitude), with a view down a valley. On inspection, the formation turned out to be an "intelligent" sketch of the actual Mandelbrot Set. This was not an accurate rendition applying the necessary mathematics "in the field", but an almost symmetrical drawing, with the big body of the Mandelbrot being a circle of which two sections has been deleted by drawing two circles at off the Mandelbrot's "head", which was also a near circle with another on top of it. Surprisingly the "mini" Mandelbrot 18 meters away was only a single circle. Scaled properly, it would have been a 12 inch circle 17 metres from the main formation.
The set is so fundamental in nature that it can manifest itself naturally (much like a geometric crystal), so that the inconsistencies between actual and formation sets could not be brought about by 'tampering' with the necessary mathematics. In the construction of a crystal, nature omits a corner or produces a fault the grittiness of nature creeping in but if formed naturally, there is no way that a 'baby' set can be changed into an oversized circle. The Mandelbrot Set is fundamental, unique and as one with itself. There is no way for a gritty quirk to modify the mathematics which tended to show an intelligent creator in the field. A further testimony to intelligence, was the 'judgement' involved in forming a circle rather than the Baby Mandelbrot Set.
Accounting for the 14 inch circles bordering the hard shape, we have to assume that the formation of the Baby set was possible. We can see that a judgement was made to conserve effort as the principle message had been displayed in the main formation.
The Detail
The largest part of the formation was the 'heart shape' with a normal circle lay but pinched inwards at the base so the lay navigated a sharp and perfect angle at the pinch. Also rather strange was a perfect overlaid 5 inch bar of lay projecting from the swirled centre perpendicular to approximately half of the "heart" diameter along its negative imaginary axis, and geographically towards the centre of Salisbury Plain and Stonehenge. There were no pole marks at the centres of any circles, just patches of smooth bare earth 5/ 6 inches in diameter. The centres of swirl lay close to the geometric centres of each circle which appeared to be particularly, but not entirely, regular. The direction of the swirl was interestingly clockwise and then anti-clockwise and so on with connecting circles.
2. The second formation was formed around the 16th of July 1992 outside Oxford(!). This was an exact copy of the Ickelton formation except it was precisely half the size. It also had the incredible smooth lay and the swirls originating from the "heart".
3. The third formation appeared near Leipzig in Germany on the night of 19 August 1993. According to reports the formation exhibits the same features of the previous two, although the size has not been confirmed yet.
Conclusion
There are various theories for the existence of crop circles, but none proven so far. Even researchers studying the phenomena for the last 20 years are still in the dark. A few hoaxers have owned up, but this does not explain the 400+ formations appearing every year in the UK alone.
Tree Maker
by Dolores García García
One of the classical examples of fractals in nature is a tree: a branch resembles the whole tree. Probably you have seen already some computer pictures with trees that look exactly like the real ones, drawn with the help of fractal programs. How do they do it? A first approximation would be to draw a line for the trunk, finish it in a random point, then draw another two lines for the two main branches, in any random point divide these two in four, and so on. But the result doesn't seem like a tree at all; it doesn't even look like a plant.
The most obvious reason for this is that, in real trees, branches become shorter in each division. But after correcting this the program doesn't produce trees, either. In the best case, we could say it makes models of algae.
After observing a few real trees, it's easy to notice that their structure is a bit more complex. When a branch divides in two, one of them follows almost the same direction of the main branch, while the other makes an angle, and is usually shorter. This angle is a constant for any given tree. Besides, there is a relation between the angle and other parameters. In trees like the larch, with a right angle, the length of the trunk without branches and the space between two consecutive divisions are quite small, and secondary branches are considerably shorter. On the other hand, the plum tree, with a much smaller angle, has a longer trunk, there is more space between divisions, and primary and secondary branches have almost the same length.
This relation is expressed in the program with the variable TREE. Values of TREE next to 1 produce larches, while values next to 0 produce plum trees, or even genistas.
But the program is far from perfect. It still produces many things that can't be called trees. Any suggestions to improve it will be welcome.5 REM **********TREE MAKER************
6 REM ****by Dolores García García****
7 REM Corredera de San Lorenzo, n.1, 2A
8 REM 15706 Santiago
9 REM SPAIN
10 RANDOMIZE
20 DIM X(256):DIM Y(256)
30 TREE=RND:P=1:PI=3.141593
40 XO=160:YO=200
50 X0=RND*6-3:Y0=50/(SQR(TREE)+1)
60 X(0)=X0/2:Y(0)=Y0/2
70 X(1)=X0:Y(1)=Y0
80 CLS:SCREEN 1:KEY OFF
90 PSET (XO,YO)
100 LINE -(XO+X0,YO-Y0)
110 ALFA=TREE+RND*PI/6+PI/12
120 L1=.85+TREE/5:L2=1/(TREE*.75+1)-.1
130 FOR N=0 TO 6
140 FOR M=1 TO 2^N
150 COSA=COS(ALFA):SINA=SIN(ALFA)
160 SINA=SINA*(.75+RND/2):COSA=COSA*(.75+RND/2)
170 Q=INT(P/2)
180 X1=(X(P)-X(Q)):Y1=(Y(P)-Y(Q))
190 R=SQR(X1*X1+Y1*Y1)
200 X1=X1*.9+RND*R/5:Y1=Y1*.9+RND*R/5
210 X2=X1*L1+X(P)
220 Y2=Y1*L1+Y(P)
230 PSET(XO+X(P),YO-Y(P))
240 LINE -(XO+X2,YO-Y2)
250 S=SGN(RND-.5)
260 X3=X1*L2*COSA-S*Y1*L2*SINA+X(P)
270 Y3=S*X1*L2*SINA+Y1*L2*COSA+Y(P)
280 PSET(XO+X(P),YO-Y(P))
290 LINE -(XO+X3,YO-Y3)
300 X(2*P)=X2:Y(2*P)=Y2
310 X(2*P+1)=X3:Y(2*P+1)=Y3
320 P=P+1
330 NEXT M
340 NEXT N
Complex Probability Beziers of Three Polynomials
In Iteration Time
by Roger L. Bagula (B.S.CHEMISTRY U.C.L.A.'68)
In going through Mal Lichtenstein's Amiga Basic programs I came on the Kosko fuzzy logic fractal. In thinking on that kind of probability I came up with the idea of using the complex z in a Mandelbrot mapping as an extended probability variable in a Bezier morphing of the iteration(time) variable k. My first experiments used raw k but I found the ratios k/kmax and k/sqr(kmax) worked much better. Now, most of you will say but probability is limited to the real domain {0 to 1},right? That's not true if you think of it as a probability density with density over a complex domain.
What results is the ability to morph time domain polynomials in sets over a Mandelbrot mapping of probability density saturation. I used the three functions on k'=k/sqr(kmax) as {k'^3,k',k'^2} with Bezier densities of {z^2,2*z*(1-z),(1-z)^2}.That it worked to give a nice new fractal says to me a new method is born for seeing time functional changes on a probability density morphing. It would also appear to be a new sort of what I have been calling Kaluza-Klein fractals of the Mandelbrot mapping.
What it amounts to is having the three fixed fractals and observing time change iterations morph them into totally new shapes. The practical use seems to be to find polynomials that taken as a set nearly balance each other. For instance, the set { 1/k',k',k'^2} don't balance at all well and give a very small fractal at |c|<1. To me the discovery that fuzzy logic can take on complex as well as real values is a revelation in how I will see probability in the future! We are apparently only able to see the real part of some of the more complex probability problems nature offers, but quantum mechanics has been dealing in this sort of probability for a long time as "density" equations in Hilbert space. The saturations I am seeing are of fractal Hausdorff dimension and must be thought of in my extended Hilbert space I have called Mandelbrot space. © R. L. Bagula 29 Sept 1993
AMOS BASIC PROGRAM:
Screen Open 0,640,400,16,Hires
Screen Display 0,129,30,640,400
Print " Input file save name"
Input S$
Curs Off : Cls 0 : Flash Off
Locate 0,2 : Pen 15 : Paper 0
N#=400 : M#=640 : Dim H#(10)
For I#=-3.0 To 3.0 Step 6.0/(N#)
D=D+1
For J#=-3.0 To 3.0 Step 6.0/(M#+0.5)
C=C+1
A#=I# : B#=J# : K#=0 : D#=Sqr(A#^2+B#^2) : R#=D#
Repeat
If K#=0 Then F#=A# : G#=B# : R#=D# : E#=A# : W#=B#
K#=K#+1: L#=R#: X#=F#: Y#=G#: E#=K#/Sqr(150)
F#=(X#^2-Y#^2)*(E#^3-2*E#-E#^2)+2*X#*(E#-E#^2)+A#
G#=2*X#*Y#*(E#^3-2*E#-E#^2)+2*Y*(E#-E#^2)+B#
R#=Sqr(Abs(F#^2+G#^2))
Until Abs(L#-R#)<10^-3 or K#>150 or R#>=Sqr(150)
If F#=0 Then F#=1
If R#=0 Then R#=1
Z=Int(K#+Abs(K#*Ln(1+D#/(R#^2))+W#*Atan(G#/F#)))
Ink 1+Z mod 15
Draw C,D To(C+1),(D+1)
If C>M# Then C=0
Next J#
Next I#
Save Iff S$
End
Random And Pseudo-random Walks
By Roger L. Bagula
In doing research on the theory of events that appear as if they have no rule for order or magnitude of their statistical occurrence, I came upon the "drunkard's walk". I found it in economics and statistical mechanics. I also found it in artificial intelligence in "path finding algorithms" in which a goal was found using a rule and a random walk. My random walk uses a polar normal random I found in an old Byte I have lost, now ,or I would give a good reference. The AMIGA BASIC program in 611 by 185 screen is:
PRINT "input relative amplitude"
INPUT v
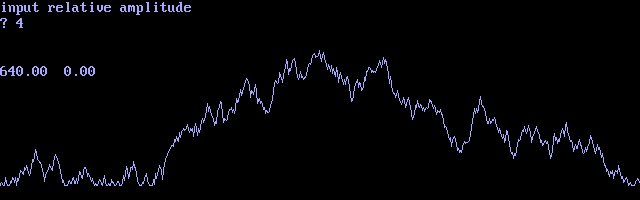x1=0:y1=0
RANDOMIZE 32000
FOR x= 0 TO 611
GOSUB 200
y=y+b*v
IF y>185 THEN y=185
IF y<0 THEN y=0
LINE (x1,185-y1)-(x,185-y),1
LOCATE 5,1:PRINT x,y
x1=x:y1=y
NEXT x
END
REM POLAR RANDOM SUBROUTINE
200 v1=(1-2*RND)/SQR(2)
v2=(1-2*RND)/SQR(2)
s=v1^2+v2^2
IF s>1 THEN GOTO 200
s=SQR(-2*LOG(s)/s)
b=v1*s
RETURN
This kind of program works after a fashion. I have done some "spectrum chaos" work using Bagula projections and the following program again in AMIGA BASIC gives a "pseudo-random" effect that is "deterministic":
REM Bagula projection with Sierpinski spectrum
REM as pseudorandom walk R.L.BAGULA 16 SEPT '93
PRINT "input relative amplitude try 1 to 5"
INPUT v
PRINT "input relative x scale try 1 to 8"
INPUT w
x1=0:y1=0:z1=0
FOR x= 1 TO 611
GOSUB 200
y=y+b*v
IF y>185 THEN y=185
IF y<0 THEN y=0
z=z+a*v
IF z>185 THEN z=185
IF z<0 THEN z=0
LINE (x1,185-y1)-(x,185-y),1
LINE (x1,185-z1)-(x,185-z),3
PSET(611/2+20*a,185/2+20*b),1
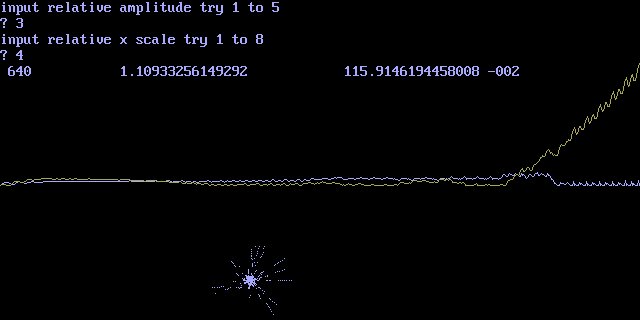LOCATE 5,1:PRINT x,y,z
x1=x:y1=y:z1=z
NEXT x
END
200 b=0:a=0
x0=(x MOD (w*3.1415927#))/w
y0=(y MOD (w*3.1415927#))/w
FOR k=1 TO 12
s=LOG(2+k)/LOG(2):v=2-v
b=b+2^(-s*k)*3^(v*x/611)*5^(-y/185)*SIN((2^k)*x0)*COS((5/3)^k*y0)
a=a+2^(-s*k)*3^(v*x/611)*5^(-y/185)*COS((2^k)*x0)*COS((5/3)^k*y0)
NEXT k
RETURN
I have used a "pi" scaling function and three constants with d=3=s+v+1.The result at times appears as random or more random than the random walk program. The spectrum is Sierpinski in nature, but you can try a von Koch {s=log(3+k)/log(3)} if you like. I like the 5,8 scales for showing the random appearance well. The question becomes: "Can one 'curve fit' these functions to actual observed events? " I think they may be easier to fit than random walks, for sure!
Dr Mandelbrot has done some cotton futures work using fractals, but this "spectrum chaos" using Mandelbrot space functions is a little beyond that work, I think, in complexity of the dimensionality used to fit the functions. The whole problem of "prediction" is changed by people being able to predict the next value of a variable in economic markets. Suppose you have two or more people "betting" on the fit they have by a game plan using computer trading, then it becomes not a random walk or a Mandelbrot space function, but a games theory problem! The larger number of people plotting and betting the less like an "ideal" free market it becomes. In predicting other statistical mechanics problems it may be better suited since you don't have as big an "human" factor.
The way I would go about fitting these is to start with the best estimate of the "period" the data shows of the major oscillation. Then, I would adjust the amount of amplitude at each iteration. Last, I would adjust the dimensionality spectrum if necessary. I wish I could say that you could do something like a linear regression to get a fit, but to start it will be an art more than a science. Doing fast Fourier analysis of the data can help if the result is analyzed right: the result is dependant on both the time and the event space itself. Is this a Markovian string type of function? It seems to have that kind of iteration dependence in it as well as the dimension dependence.
Am I getting through to you reader? We are talking about being able to predict "futures" on stuff that was thought "totally" random and in the realm of probability for the last generation of scientists. (©R.L.Bagula 16 Sept 1993)
B.C.S. Superconductors, Renormalization
and Yang-lee Theory
by Roger L. Bagula
In trying to write a letter in answer to James Isaac on "superconductors", years of study finally came together. I have beside the computer a stack of five books that served as source material, but I finally "got-it"! The way I see it at this moment is that Yang-Lee renormalizations work not only on "magnetizations" in Heisenberg spin theory, but also on "order parameters" in B.C.S. theory (J. Bardeen, L. Cooper, J.R.S. Shrieffer, Phys.Rev.,108,1175,1957).
So where is the "beef"? The Yang-Lee equation from page 170 of Terrill L. Hill, Statistical Mechanics (Dover) is:
1) ln(Z)=sum(k=1 to kmax)ln(1-z/zk)
Reorganizing for a single iteration: c=zk
2) z"=z*(1-z/c) : Mandelbrot quotes z"=c*z*(1-z) in The Beauty of Fractals
It was the work with the "ergodic gauge" fractals that with Landau phonon interactions gave me the key. Terrill Hill on page 329 gives for a d=2 "lattice gas":
3) tanh(K)=exp(-2*K) :K=E/k*T
with solution e0=0.4407*k*Tc.This is very like the B.C.S.:2*e0=3.57*k*Tc. The factor of four between them is very nice! So how do I get an Hilbert space-like phonon into a Yang-Lee iteration? My idea is to put it in the second term only:
4) z"=z*(1-z/c+M*r*exp(i*k*atan2(cb/ca)/|c|): M is ordering magnitude
With a term like that it should take longer to reach "saturation" at the zmax limit of the iteration. Notice that the Landau term is Hilbert-like, not Weierstrass-like! To bring this into the Hausdorff-Mandelbrot era: (a,s) are renorm constant and dimension.
5) z"=z*(1-z/c+M*r*exp(i*(a^s*k)*atan2(cb/ca)/|c|): M is ordering magnitude
The antiferromagnetic Potts spin hierarchical renormalizations are very like B.C.S.spin pairings: my way of iterating these is to use the q term as the c term in the Mandelbrot mapping:
6) z"=[(z^3+3*(c-1)*z+(c-1)*(c-2))/(3*z^2+3*(c-2)*z-3*c+3)]^2
That's from page 146 of The Beauty of Fractals. A few years back I did this iteration in a fit of energy: the separation of the complex terms is a real bitch! Now, how do I get a phonon into this type of lattice? My guess would be to do a two step like I do in the supercalculus transform in which the phonon term is added to the last z term:
7) z=z(last)-r*exp(i*k*atan2(cb/ca))
That z, then, goes into the Potts spin iteration. Since at c=z(last) for k=1 you always start at z=0:
8) z(k=2)=[(c-1)*(c-2)/(-3*c+3)]^2=(c-2)^2/9=c^2/9+4*c/9+4/9
So it starts off different than most Mandelbrot mappings in the phonon interaction. In the ergodic gauge since a^(s*k)<>1, this is not true:
9) z=z(last)-r*exp(i*(a^(s*k)*atan2(cb/ca))
The difference will have to be shown experimentally, but it begins to show up on the first iteration. Adding a magnitude M can make them closer for the first two or three terms. In general,if B.C.S. theory breaks down even with phonons adding instead an ergodic gauge term can give better solutions at higher magnitudes of interaction between the "fluid" of the lattice gas of electrons because it acts more like real electrons do. The metal clusters that make up the high temperature superconductors have "Fermi surfaces" that change their interactions with the external world as the temperature changes.Crystal structures can help to calculate these surfaces and give "real" renormalization pictures. (R.L.Bagula © 2 SEPT 1993)
Phonon-yang-lee Program in Amos Basic:
Screen Open 0,640,400,16,Hires
Screen Display 0,129,30,640,400
Print " Input file save name"
Input S$
Curs Off : Cls 0 : Flash Off
Locate 0,2 : Pen 15 : Paper 0
N#=400 : M#=640 : Dim H#(10)
For I#=-6.5 To 2.5 Step 9/(N#)
D=D+1
For J#=-4.5 To 4.5 Step 9/(M#+0.5)
C=C+1
A#=I# : B#=J# : K#=0 : D#=Sqr(A#^2+B#^2) : R#=D#
Repeat
If A#=0 and B#>0 Then T#=Pi#/2
If A#=0 and B#<0 Then T#=-Pi#/2
If A#>0 and B#>0 Then T#=Atan(B#/A#)
If A#>0 and B#<0 Then T#=Atan(B#/A#)
If A#<0 and B#>0 Then T#=Atan(B#/A#)+Pi#
If A#<0 and B#<0 Then T#=Atan(B#/A#)-Pi#
If B#=0 and A#>=0 Then T#=Pi#/2
If B#=0 and A#<0 Then T#=-Pi#/2
If K#=0 Then F#=A# : G#=B# : R#=D#
K#=K#+1
L#=R#
X#=F#
Y#=G#
E#=1-R#*Cos(T#)/D#+(R#*Cos(K#*T#)/D#)/0.6873999
W#=R#*Sin(T#)/D#-(R#*Sin(K#*T#)/D#)/0.6873999
F#=E#*(1-E#)+W#*W#
G#=-E#*W#+W#*(1-E#)
R#=Sqr(Abs(F#^2+G#^2-K#^2))
Until Abs(L#-R#)<10^-3 or K#>150 or R#>=Sqr(150)
Z=Int(K#)
Ink 1+Z mod 15
Draw C,D To(C+1),(D+1)
If C>M# Then C=0
Next J#
Next I#
Save Iff S$
End
by Yvan Bozzonetti
The C3FBC4 formula comes from my Fractint cos1.frm file. I have published that file before in Fractal Report, but it is hard to see what we can wait for from the dry formulae. Without a fast PC, testing may be cumbersome. So I concentrate here on a single formula. It is:
Z = A*COS(Z^B)^C+D
In this particular case, we start with Z=A=D=pixel. B and C are respectively the P1 and P2 complex parameters. Now we can start our travel in chaotic mathematics. Put first the inside colour value to 0 in the X selected menu.
It was a new Moon night (try all parameters to 0 or look for first picture: cos1_001.jpg)
with plenty of mysteries and adventure to come. When I am typing this exploration
account on an old PC, a nearby 486DX give me a look at the mathematical night. The real
part of C (first line of P2) give a bigger Moon for positive values and a smaller one for
negative entries. Beyond -6 there is nothing to see on the screen without the zoom
function.
The first P1 line with small positive values return too a bigger Moon (all other
entries remain at 0). Is this formula really uninteresting? What with real
negatives P1 values? At -1, something happen: A bilobed hole appears inside the
black Moon. (See COS1_002.jpg). The hollow Moon or world is a well known
initiated subject, what about larger absolute values such -2.5? COS1_003
produces a five lobes inner space; we guess the lobe number is two times the
absolute value of the parameter. Minus four will produces 8 lobes, -15 will generate 30 of them, any
fractional value such -3.3 will generates a shrunken lobe to complement the normal set. Well, we have at
the same time something interesting to look at and some understanding of the formula behaviour.
For positive values fairly large, another pattern starts to reveal itself.
P1=3 returns an indented Moon with four craters on the limb
(COS1_004.jpg).
P1=4 puts "orbital" elements and a
black cover on each crater
(COS1_005). With P1=6
(COS1_006) and P1=12 the
underlying logic appears. All of that
is rather simple fractal patterns, can
we combine the known elements to
get more? Sadly, the most interesting
pictures are produced by positive
and negative real P1 values, we can't
mix them in a single picture.
A thing to try is a positive real P1 value with a negative P2 one, so that the Moon is reduced. P1=7 and P2=-4 give the COS1_8 display...
And the door of hell opens. There is a temptation to fall in this screen and zoom on
some part of it (COS1_009). There is an isolated luminous point in the upper part of
the screen, it look as the sole living window of a haunted castle. No! we ought not
fall in the hell zoom, at least for some time.
A larger absolute negative on P2 must reduces further the central Moon; with P2=-20, COS1_01O seems invalidate that guessing.
The solitary light of the ghost comes back to the memory, can we dive in the deep of
hell? If you have not a fast computer, don't try the zoom key on COS1_11, you
would remain frozen in hell for some very long time.
Using positive imaginary P1= 0.6 gives a first break in the Moon centre
(COS1_12.jpg). With P1=1.5, the formulae logic starts to reveal itself
(COS1_13.jpg)
The display using negative imaginary P1 numbers shows the upper part of the Moon, not the lover one, is progressively destroyed.
Using both, a negative real P1 value and a positive imaginary part, grinds three quarters of the original circle, picture 16 displays an example. To save a lower quarter, try a negative real part of P1.
Imaginary P1 and real P2 girds the four quarters of the circle (COS1_17) with interesting results and some options to go to the zoom key. The same can be said of the imaginary P1 and P2 combination of picture 18. There are two more pictures coming from the cosz.frm file with 600 x 800 SVGA format.
The cos1.par file contains fifty entries, you can start with pictures number 28, 32 and 38, at least that is my personal choice. Most of the other are entry in a particular formulae, they are worth as a starting point to zoom in or out. For each formulae you can start an exploration similar to the one summarized in the cos.jpg pictures.
A word of caution about using the cos1.frm file: it work well with my PC 486 DX 33 and both Fractint 16 and Fractint 18, unfortunately any correction or addition to it don't work with Fractint 18. (there is no problem with version 16). On my PC 386 DX 25 the file don't work on Fractint 18, there is no difficulty with version 16. On my PC 386 DX 40, the version 18 don't accept the mathematical coprocessor, nor COS1.FRM on version 18, the same file encounters no problem with version 16 once more. If you can't run some files, I think the simplest action is to load some old Fractint release. I have not tested Fractint 18.1 to this day.
Letter
If the Fractal subject looks as a too narrow domain, I suggest something as Mathematical Display Report or may be the less awful: Display Report.
About programming music, I think I am near a solution: Mathematica from Wolfram Research has that capacity, unfortunately, that software sells for more than � 1000. (at least in France).
If FR has a small circulation, it may be possible to include in it some pages from a PC printer. I think about a colour printer... Colour is the most interesting element in fractal display. Another solution would be to turn to a disk magazine or a disk supplement for coloured elements. To be sure, disks would be paid by subscribers. A cheaper solution yet: to put everything on a PC with modem and BBS software, subscribers not interested in sending disks or money for them, could use the BBS with some part free and some needing a paid subscription. At the next step, the BBS could be linked to Internet, this is a place to find many fractal interested amateurs. To summarize, a subscriber could start with a paper edition including one or two colour pages, then he (she) could turn to the disk complement or the BBS solution with a modem. In the final stage, an entry on Internet would allow more services...
Comment
The problem with implementing these ideas is time. Colour printers take serious time to print one side of an A4 sheet, not to mention the cost. Disk copying is very time consuming unless an expensive duplicator is used. Rather than get involved with communications, which is very expensive to run, I'd rather save up for a much faster computer!
Seriously though, there are several fractal areas in Compuserve and other bulletin boards.
Get your own Free Home Page