Journal of the Operational Research Society (1995) 46, 562-578
CAUSE, EFFECT, EFFICIENCY
AND SOFT SYSTEMS MODELS
FRANK GREGORY
School of Industrial and Business Studies
University of Warwick
The logical connectives in the conceptual models of Soft Systems Methodology are limited to relations of "necessity". This is not enough to achieve a correspondence with states of affairs in the physical world. In order to attain this correspondence connectives representing "sufficiency" must be included. When this is done a logical account of efficiency is possible. This defines efficiency as the arbiter between two or more sufficient but unnecessary conditions of a desired effect.
Key Words: Information systems, Soft Systems Methodology, Modelling, Logic, Efficiency, Systems.
During the last decade Soft Systems Methodology (SSM) has had considerable success as a general purpose problem solving methodology. The ability of SSM to address unstructured (soft) problems can be contrasted with traditional O.R. which aims at solving structured (hard) problems. Although there is a contrast this does not amount to an incompatibility. During the process of SSM analysis a soft problem will often turn into a hard problem which can be solved by structured methods.
A key device in SSM is the development of a conceptual model. This type of model is not intended to represent what exists but to represent a view of what could exist. The difficulty here is that having constructed a desirable conceptual model there is no guarantee that it will correspond to anything that actually can exist. In most uses of the methodology this does not matter as the primary aim is a change of perspective on the part of those concerned rather than a change in a state of affairs in the physical world. However, the models are sometimes used as the starting point for the design of information systems intended to support physical processes. In these cases a correspondence between the models and the physical world is required.
This problem can be solved by a method which can also act as a link between SSM and structured information system design [1], [2]. Similarly the solution can act as a link between SSM and traditional O.R. The problem, its solution and the implications for O.R. are discussed in four sections.
In the first section an analysis of the logical status of SSM conceptual models is undertaken. It is suggested that a correspondence between the models and the physical world will hold if two conditions are met. Firstly, the terms or elements of the model must refer, directly or indirectly, to objects or events in the physical world. Secondly, the relations between the terms or elements in the models must have the same logical form as the relations that hold between the objects and events in the physical world. In respect of this last condition, SSM models are inadequate. The elements in the models are connected only by relations of necessity. Relations of sufficiency are also required in order to match the causal sequences in the physical world.
The second section shows that sufficiency can be introduced into the models without difficulty. With this additional relation a logico-linguist model is produced which is exhaustive and capable of representing any conceivable state of affairs.
Section three considers applications resulting from the fact that a logico-linguistic model functions as a conceptual cause and effect diagram. The ability to represent all logical possibilities in a cause and effect sequence gives the model greater scope than the empirical models that tend to be used in quality control.
The fourth section discusses applications concerning efficiency. In SSM, a criterion for efficiency is one of three measures of performance that accompany every system, but it is not clear what this criterion is meant to operate on. It is suggested that efficiency can operate as the arbiter between two or more conditions that are sufficient for a desired effect. This gives efficiency a systemic and logical role that can be complimentary to quantitative accounts of efficiency in terms inputs and outputs.
CONCEPTUAL MODELS IN SSM
General descriptions of Soft Systems Methodology (SSM) are highly diverse. SSM has been characterized as a learning system [3], part of a new paradigm for O.R. [4] and as a front-end for information system design [5]. However, such diversity is to be expected considering that its aim is to address any kind of unstructured "soft" problem in any organizational or social context.
SSM functions as a learning system because it facilitates a greater understanding of the problem situation on the part of those concerned. By bringing out the world views (Weltanschauungen) of the people involved in the problem situation, SSM can produce various types of result: the problem might simply disappear as the result of a consensus; a fairly unstructured solution might result, such as agreement to adopt a new role for the organization; a third possibility is that the problem becomes structured, in this case a soft problem resolves into an identifiable "hard" problem. It is this third type of result that will be the subject of this paper.
The classic SSM method is a seven stage process comprising: (1) entering the problem situation, (2) expressing the problem situation, (3) formulating root definitions of relevant systems, (4) building conceptual models of Human Activity Systems, (5) comparing the models with the real world, (6) defining changes that are desirable and feasible, and (7) taking action to improve the real world situation. [6 - 8].
The dynamics of the method come from the fact that stages (2) through (4) are always an iterative process. The stake-holders (defined as Client, Actors and Owner) engage in a debate guided by the analyst/facilitator. During this debate various root definitions (succinct statements of appropriate systems) and conceptual models are put forward, modified and developed until a desirable model is achieved by consensus. This model then forms the basis for real world changes.
The conceptual models, therefore, have a vital role and it essential to understand that they are "notional"; they are not intended to represent an existing state of affairs.
"It cannot be emphasized too strongly that what the
analyst is doing, in developing a HAS [Human Activity System conceptual] model, is not trying to describe what exists but is modeling a view of what exists." [8]
The name "conceptual model" is ambiguous. It could mean a model of concept or it could mean a model that is conceptual. Wilson would seem to be saying that the SSM models are intended to be models of concepts. However, it is worth reflecting on the difference here.
We can distinguish between what models are and what models are models of. With the exception of iconic models, such as a scale model of Winchester Cathedral, most models are concepts. But they are, mostly, intended to be models of real world states of affairs. The value of a model is usually directly proportional to how well it corresponds to a past, present, future, actual or potential state of affairs. A model of a concept is quite different because in order to be a good model it need not have this real world correspondence.
One of the features of modeling concepts is the ability to represent notions that have no easily defined physical equivalent. Rules, laws, values, and judgements can easily be represented. This, plus the ability to represent, compare and integrate various Weltanschauungen, gives models of concepts tremendous scope. This scope must always be greater than the scope of a model of a physical state of affairs for the simple reason that models of concepts are limited only by what is conceivable. As no model of a physical states of affairs can be inconceivable, every model of a physical state of affairs must be capable of being paired with a model of a concept.
This unlimited modelling scope allows Checkland to achieve solutions that could not have been identified using models of actual states of affairs. This is particularly true where the problem has been non-physical i.e. a problem about goals, gaining a consensus, values etc.
Models of concepts and the physical world
In SSM it is not clear what sort of relationship can exist between a conceptual model (in the sense of a model of a concept) and the physical world.
When a physical solution is required to resolve a problem situation, Checkland does not, in practice, take the models far beyond a general description. This is clear in the results of case studies. In Checkland and Scholes Soft Systems Methodology in Action [7] the outcome of the case studies are described as changes in thinking or perspective, changes of role for the organization as a whole, problem identification, or what has been learned about the organization. While these changes in thinking have lead on to real world changes such as detailed organizational restructuring and new information channels, the real world changes were not specified by the methodology.
By contrast, the case studies in Wilson's Systems: Concepts, Methodologies and Applications [8] come up with specifications for new information processing procedures intended to support physical processes. This implies that there must be some relationship between the conceptual model and the information system; just as there must be some relationship between the information system and the physical process.
There is a prima facie dilemma here. What has been said so far is that a conceptual model need not be based on anything in the physical world. If this is so, then it would seem to follow that there can be no guarantee that a desirable conceptual model will ever correspond to anything in the physical world. The literature of SSM is not enlightening on this point. It is not clear how the transition from a model of a concept to a change in the physical world is effected. At stage (4) in the methodology we have a model of a view of what exists, but a view of what exists might bear no relation at all to what actually exists. In this case, the model can be no help in taking action to improve the real world situation as is required in stage (7).
The most simple solution to the dilemma is to take the conceptual models to be a number of inductive hypotheses connected together.
Given this, the models would be empirical and could be tested against events in the real world. However, this would mean that they are not models of concepts but models of putative physical states of affairs. As such they would not be significantly different from most other types of model.
A second solution to the dilemma is more difficult. This is to take the conceptual models as being logico-linguistic models. On this interpretation model building is a type of Wittgensteinian language game in which the stake-holders create an agreed language for describing the problem situation. The iterative process enables the sense (connotation, intension) of the various terms in the models to become fixed, thereby establishing a syntactical structure. In this way the models are analogous to formal systems such as arithmetic.
There are two requirements for a formal system to correspond to the physical world. The first is that its terms should have direct or indirect reference (denotation, extension) to objects, events or states or affairs in the physical world. The second is that the functional connectives should be capable of reflecting the behaviour of objects, the sequence of events or changes of states of affairs in the physical world. In arithmetic the terms are numbers, the functional connectives are addition, subtraction etc. In SSM models the terms are contained in the bubbles and the functional connectives are the arrows between the bubbles.
Exactly how reference is established has been the subject of ongoing debate among some of the world's most eminent philosophers and logicians for nearly a century. However, although reference is difficult in theory it tends to be unproblematic in practice. If people can agree about the sense of a word there is usually no problem about establishing whether it has reference or not. In the present case, sense is unproblematic because it is established by building the model.
This leaves the second requirement. The most general principles governing the behaviour of objects, the sequence of events and changes of states of affairs in the physical world are the laws of cause and effect. The remainder of this paper will show firstly, that the connectives in SSM models do not reflect the laws of cause and effect, secondly, that this shortcoming can be easily avoided by a modification of the models, thirdly, that such modification could have interesting applications.
DEVELOPING THE LOGIC OF CONCEPTUAL MODELING
The logic of Soft Systems models
According to Checkland and Wilson the SSM modeling language consists of English verbs. These are formulated into elements which express commands. This has the advantage of being easily understood by the stake-holders in the client organization and this is essential as their participation is a fundamental requirement in the development of the model.
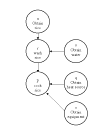
The connectivity between the elements is defined as "logical dependence".8 Thus, in Figure 1, r is dependent on u and v. This supports the view that the SSM conceptual models are intended to be models of concepts, rather than models of physical objects or events, because logical relations cannot exist between physical objects or events.
There is a problem here because the elements of the SSM models are commands and generally accepted logics only operate on truth bearers. Statements, or more strictly propositions, can be true or false and are, therefore, truth bearers. Commands can be neither true nor false and have no place in generally accepted logics. A logic of commands, an imperative logic, has been discussed by some authors 9 but Probert 10 finds that an imperative logic is not enough to fulfil the role required of it in an SSM model.
This problem can be easily overcome by replacing the imperative phrases in the models with declarative phrases. Instead of putting "wash rice" we could put "the activity wash rice has occurred" and now the truth of this proposition could be said to be dependent on the truth of the proposition "the activity obtain rice has occurred". Or, more concisely, we could say "rice is washed" instead of "wash rice" and "rice is obtained" instead of "obtain rice". Figure 2 shows how the commands of Figure 1 can be replaced by propositions.
Accounts of the logic of causation are in terms of necessary conditions, sufficient conditions and necessary and sufficient conditions. 11-14 Logical dependency, which is the only relation used in SSM models, is parallel to a necessary condition. If the truth of the statement "rice has been washed" is logically dependent on the truth of the statement "water has been obtained", then obtaining water will be a necessary condition of washing rice. However, the relation of logical dependency does not amount to sufficiency; obtaining water is not sufficient for washing rice.
In Figures 1 and 2 if we say r is logically dependent on u and v we are saying the same thing as saying u and v are necessary for r, but this does not mean that u and v are sufficient for r. The logical way of expressing this is to say that r implies u and v. In symbols:
r --> (u & v)
Here the truth of r allows us to infer the truth of u and v. However, the truth of u and v does not allow us to infer anything about r. In causal terms the fact that r happens means that u and v must have happened but the fact that u and v happen does not mean that r will happen. If we think of the arrows as representing implication, as they do in symbolic logic, then the arrows point the wrong way in SSM models. The upshot of this, in simple English, is that the fact that rice and water are obtained does not mean that the rice gets washed.
This entails that a physical system that is based on a model that contains only necessary conditions can never be guaranteed to work. It may work because the necessary conditions may in fact be sufficient but it is also possible that they might not be.
This deficiency can easily be remedied by adding another condition that, in conjunction with the existing conditions, forms a set which is sufficient. The way this can be done is shown in Figure 2 (a). Here the set comprising w and u and v is sufficient for r. As each of these conditions (w, u and v) is also necessary for r, the set is a necessary and sufficient condition (N&S condition) of r.
In Figure 2 (a) the new elements are agents which could correspond to people, machines or, in the case of an information system, a computer programme. Traditional SSM models are models of human activity systems and it is reasonable to think that implicitly the presence of a human agent has been assumed.
The introduction of N&S conditions solves the problem of insufficiency but deficiencies in the model remain. Necessary conditions and N&S conditions show only one way in which the objective can be attained. For example, if we want to obtain equipment this could be accomplished by buying it or making it or borrowing it.
Wilson recognizes this and tries to accommodate it by making between what is to be done and how it is to be done. The how can be expanded in two ways: by showing greater detail (in effect, more necessary conditions) or by showing different possibilities.
Mingers [15] has shown that the what/how distinction is not, in itself, capable of making the distinctions that are required. One problem is that the expansion of the model by taking it to a higher resolution level, which is similar to the way data flow diagrams are decomposed, will fail to make clear whether the model is being expanded in order to show greater detail or whether it is being expanded to show one of a number of possibilities.
Mingers suggest a qualified what/how distinction as the basis for the development of the two hierarchies, one to show greater detail and one to show different possibilities. There is, however, another way of introducing different possibilities into the models; this involves the introduction of a third logical connection.
So far we have two types of logical connection:
A --> B. Which means A implies B. This corresponds to B being a necessary condition of A.
A <--> B. Which means A implies B and B implies A. This corresponds to B being an N&S condition of A, and, as a logical consequence, A being an N&S condition of B.
To this group we can add:
B --> A. Which means that B implies A, or that A is implied by B. This corresponds to B being a sufficient but unnecessary condition (SUN condition) of A. SUN conditions are indicated by broken lines in Figure 2B.
It is self evident that if it is true that polished rice is obtained then it will be true that rice is obtained. We can, therefore, say that obtaining polished rice is a sufficient condition of obtaining rice, and that "polished rice is obtained" implies "rice is obtained". While the truth of "polished rice is obtained" is a sufficient condition of the truth of "rice is obtained" it is not a necessary condition because rice can be obtained without obtaining polished rice, in the case in point rice can be obtained by obtaining unpolished rice.
The SUN conditions for any event, or for the truth of any proposition, form a set. The occurrence of the event or the truth of the proposition does not entail that any individual member of the set obtains or is true; however, it does require that at least one member of the set obtains or is true. This means that if we know that u is true then one of c, d, e and f must be true, if this is not the case then the set of SUN conditions for u (the set comprising c, d, e and f) will not be exhaustive. If the model is not exhaustive then it cannot be universal and cannot account for every case. The way to make sure that a model is exhaustive is to make sure that each set of SUN conditions cover all possibilities.
In Figure 2B, c and d cover all the possibilities for b. That is, if polished rice is obtained then the rice that is obtained must be domestic or imported. There is no other possibility, therefore, c and d form an exhaustive set of SUN conditions for b.
The break down of q, in Figure 2B, has deliberately been left so that it is not exhaustive. It is reasonable to think that if rice can be cooked with borrowed equipment it can be cooked with stolen equipment. Therefore, "equipment is stolen" is a SUN condition of q. The easiest way to correct this is to include "equipment is stolen" as an additional element. However, in many cases the stake-holders would not want to consider the possibility of stealing being part of their system. Fortunately other solutions are possible. We can omit stealing from the model but still make it exhaustive by altering p from "rice is cooked" to "rice is cooked by legal means". In this way the models begins to become linguistically as well as logically dynamic.
A third possibility is to take it that "legal means" is part of the Universe of Discourse for the system. That is, we can take it that the model is not intended to cover all possibilities but only to legal possibilities. This limitation could be recorded by amending the root definition to include legality. This going back to modify the root definition following an inadequacy in the model would be undertaken as part of the iterative process. The interrogation of the stake-holders' concepts is a large part of what the model building is about.
With the inclusion of necessary, N&S conditions and SUN conditions conceptual models are capable of representing any conceivable cause and effect sequence. These types of model will have far greater scope that models which are based directly on past experience.
APPLICATIONS OF THE MODELS - CAUSATION
Cause and effect diagrams are closely identified with the name of Ishikawa [16]. His book on quality control devotes considerable space to the subject. Ishikawa's account of causation is inadequate in two ways. Firstly, he does not distinguish between necessary conditions and sufficient conditions. Secondly, he does not take logical possibilities into account.
For Ishikawa "a cause" is broken down into other causes and these in turn can be further broken down into other causes. At any given point, therefore, it is difficult to understand what Ishikawa means when he uses the word "cause". He could be meaning a necessary condition, a sufficient condition, or a necessary and sufficient condition.
Figure 3 is taken from one of Ishikawa's cause and effect diagrams. The effect, delicious rice, is represented at the end of the main arrow. Leading into this are four arrows labelled "Pretreatment (washing)", "Raw Materials (rice)", "Equipment (cooker)", and "Second treatment (steaming)". It appears that these are meant to represent necessary conditions but it is not clear if they are meant to represent a set that is sufficient.
At the lowest level the diagram seems to list SUN conditions. The the upper right part of the diagram would seem to be saying that obtaining rice from Thailand or obtaining rice from China are SUN conditions of obtaining rice from foreign countries. However, these SUN condition could not be considered an exhaustive set unless one thought it would be impossible to make delicious rice from, say, American rice or Indian rice.
Figure 3 is one of the most comprehensive of the Ishikawa diagrams. In practice, cause and effect analysis in the Ishikawa tradition sometimes gives little more than an ordered sequence of events that have been involved in a production or distribution system (for example, see Jones & Clark [17]). Ishikawa's research method is confined to the study of the past performance of a system. Like all such work its scope is very limited. It tells us very little about what could happen nor, in a rapidly changing environment, is it likely to tell us what will happen.
The greatest advantage of logico-linguistic models over the Ishikawa type is the fact that they can cover all logical possibilities. This brings us back to the point that a conceptual model need never have a smaller scope than an empirically based model. This is because anything that is known empirically is conceivable and can, therefore, be included in a conceptual model. By contrast some things that are conceivable can never be known empirically.
Ishikawa's method developed in the context of quality control and many of his diagrams are directed at finding the causes of faults. A causal account of a fault merely reverses the logic of a desired state of affairs. If we want to achieve X, and Y is a necessary condition of X, then not Y will be sufficient for not X; to put it another way, Y will be sufficient for a fault. By the same reasoning, if Z is a sufficient condition of X, then not Z will be a necessary condition of a fault. The use of Ishikawa's models in this context does not, therefore, avoid the difficulties raised above.
Fault tree analysis is a rigorous method of fault detection used in engineering. It employs flow diagrams containing input events, AND gates and OR gates. The occurrence or non-occurrence of an input event provides the equivalent of logical negation. Given this, a fault tree is capable of representing the full range of causal conditions. For example p --> q could be expressed as (p AND q) OR (NOT p AND q) OR (NOT p AND NOT q). However, fault tree analysis presupposes a comprehensive system description 18 whereas conceptual modeling and cause and effect diagrams are meant to provide a systems description.
APPLICATIONS OF THE MODELS - EFFICIENCY
The problem of efficiency in SSM
Checkland & Scholes [7] indicate that most systems should be accompanied by three measures of performance: efficacy (E1), efficiency (E2) and effectiveness (E3).
The criterion for efficacy will tell us whether the desired effect has occurred or not. In the case of Figure 2B this will amount to whether p is true or not. If p is false we know that t or r or q or s must be false, and if r is false we know that w or u or v must be false. From this an algorithm can be formulated that will find the faults in a system and take remedial action 19. E1, therefore, has a useful role.
Effectiveness is the measure of whether the system meets a longer term aim. In the case of our example this might be to enjoy a good meal. The criterion for E1 would be is rice cooked? If the criterion for E1 is met it remains an open question whether the criterion for E2 is met. The fact that rice has been cooked does not entail that we enjoy a good meal. Better systems might be to fry potatoes, go to a restaurant or to hire a caterer. E2, therefore, also has a useful role.
Problems arise when we come to consider efficiency. Checkland & Scholes define efficiency as "amount of output divided by amount of resources used" [7]. There is a difficulty here because SSM models consist entirely of necessary conditions. If a system is to work, no necessary condition can be left out. This means that any system that consists entirely of necessary conditions can operate in only one way. Which leaves the question: what is the criterion for efficiency meant to measure?
The introduction of SUN conditions into the models can provide the role for the criterion of efficiency and, thereby, solve this problem. We can say that the system is efficient if the only SUN conditions that are true are those that meet the predetermined criterion that we have selected as E2. The criterion for efficiency can select the optimal SUN condition, or set of SUN conditions, needed to achieve E1. As a consequence it will minimize unnecessary conditions and thereby eliminate redundancy.
It is worth pointing out that there is nothing in the logic of SSM that requires that the criterion for efficiency be quantitative. In the cook rice example the criterion could be palatability. We can take the account of efficiency in terms of SUN conditions to be a logical concept of efficiency. As such it can be contrasted with the mathematical concept.
The logical concept of efficiency - an example
Figure 4 gives a model of a system to make chair legs. The input for the system is square lengths of wood and the output is round lengths with holes provided for cross piece joints.
The model serves to illustrate how time can be introduced into the models as well as showing how causes of efficiency can be identified. If the final event, p, takes place at T, then q, s, r and w must take place at T minus 1. If q, s, r and w take place at T minus 1, then u, b, a, c and v must take place at T minus 2.
There are two ways in which this system can operate. One is by drilling the holes in the square lengths and then making the lengths round on the lathe; this way invokes the w SUN condition. The other is to make the lengths round and then drill the holes; this way invokes the s SUN condition.
Given a criterion for efficiency as the number of lengths produced per day, it is quite likely that one method will conform to the criterion better than the other. It might be that difficulties in positioning a round piece of wood prior to drilling make the s route less productive. Alternatively a hole in the length might interfere with the smooth operation of the lathe, making the w route less productive.
To determine which of the possibilities is, in fact, the most efficient, would require experiment or monitoring the system in real world application. However, the important thing here is that this question of efficiency was recognized without comparison with other systems as would be required for a mathematical account of efficiency. The other important thing is that the parameters of efficiency here have been recognized without acquaintance with any real world chair leg making system. This suggests applications in a green field situation.
Mathematical concepts of efficiency
The mathematical idea of efficiency takes a system to consist of inputs, a black box and outputs. A system A will be taken to be more efficient than system B if the ratio of outputs to inputs is higher in A than in B. Data Envelopment Analysis is more sophisticated but the black box remains and, for the purposes of this discussion, it can be treated as the same as the simple input/output account.
While the mathematical concept will help to identify efficiency it does not identify the cause of efficiency. Take two systems, A and B, with comparable inputs and outputs but in which A is determined to be more efficient. Here are two possibilities as to the cause: it could be external to the systems, or it could be internal to the systems.
If the cause is a factor that is external to the system then it would seem that the cause is really an input, but perhaps one that has been overlooked. Let us suppose that A and B are farms in which the inputs are seed, fertilizer, manpower and equipment, and the output is grain. Let us suppose A does better then B because A is situated in a place where the weather is better than it is at the location of B. We do not want to say that the weather is internal to the systems as far as efficiency is concerned. This is because our concept of efficiency, unlike the concept of productivity, requires that we can make changes that can improve it. So, as we cannot change the weather we add it to the list of inputs. If the weather was the only cause of the low productivity of B, then B should now have the same efficiency rating as A.
Given this we must conclude that any true cause of efficiency is internal to the system. But if the cause of efficiency is internal an analysis of inputs and outputs cannot locate it. To identify the cause of efficiency or inefficiency of two systems would require a comparison of their internal configuration. Logico-linguistic conceptual models are one of the ways in which a system's internal configuration can be described.
The main objectives of this paper have been twofold. Firstly, to show that SSM conceptual models of human activity systems can be interpreted as models of concepts. Secondly, to show that, under this interpretation, the logic of the models can be developed to a point where it is capable of reflecting cause and effect relations in the physical world. The resulting logico-linguistic models, to a large extent, bridge a gulf between soft systems and hard O.R. This theoretical thesis has two areas of application in O.R.
The logico-linguistic models are capable of an exhaustive description of cause and effect. It has been shown that with cause and effect diagrams of the Ishikawa school this is not possible due to limited scope. These diagrams are in any case inadequate due to the fact that they fail to distinguish between sufficient conditions and necessary conditions.
With regard to efficiency it has been shown that the input/output account of efficiency is not in itself capable of identifying the cause of inefficiency and that such identification is dependent upon a logical concept of efficiency. The logic-linguistic models are capable of expressing this concept and, therefore, could, in conjunction with quantitative analysis, be used to identify the true cause of inefficiency.
ACKNOWLEDGEMENTS
The findings in this paper were the result of research funded by the Science and Engineering Research Council (SERC).
1. F. Gregory (1992) SSM to Information Systems: A Logical Account. Systemist, vol. 14 (3), 1992. pp. 180-189..
2. Y. Merali (1992) Analytic Data Flow Diagrams: An Alternative to Physicalism. Systemist (forthcoming).
3. P. Checkland (1985) Achieving 'Desirable and Feasible' Change: An Application of Soft Systems Methodology. J. Opl Res. Soc. 36, 821 - 831.
4. J. Rosenhead (1989) Introduction: old and new paradigms of analysis. In Rational Analysis for a Problematic World. (J. Rosenhead Ed.) John Wiley. Chichester.
5. G. Curtis (1989) Business Information Systems. Addison-Wesley. Wokingham, England.
6. P. Checkland (1989) Soft Systems Methodology. In Rational Analysis for a Problematic World. (J. Rosenhead Ed.) John Wiley. Chichester.
7. P. Checkland & J. Scholes (1990) Soft Systems Methodology In Action. John Wiley, Chichester.
8. B. Wilson (1984) Systems: Concepts, Methodologies and Applications. John Wiley, Chichester.
9. S. Haack (1978) Philosophy of Logics. Cambridge University Press. Cambridge.
10. S. Probert (1991) A critical study of the National Computing Centre's Systems Analysis and Design Methodology, and Soft Systems Methodology. M.Phil Thesis, Newcastle Upon Tyne Polytechnic.
11. I. Copi (1968) Introduction to Logic, Third Edition. Macmillan. London.
12. J. Mackie (1980) The Cement of the Universe: A study of Causation. Clarendon Press. Oxford.
13. D. Papineau (1978) For Science in the Social Sciences. Macmillan. London.
14. R. Taylor (1963) Causation. The Monist, 47 (2), 287-313.
15. J. Mingers (1990) The What/How Distinction and Conceptual Models: A Reappraisal. Journal of Applied Systems Analysis, 17, 21 - 28.
16. K. Ishikawa (1986) Guide to Quality Control. Second Edition. Asia Productivity Organization/Quality Resources, White Plains, New York.
17. C. Jones & J. Clark (1990) Effectiveness framework for supply chain management. Computer-Integrated Manufacturing Systems, 3 (4), 196-206.
18. R. Barlow & H. Lambert (1975) Introduction to fault tree analysis. in Reliability and fault tree analysis (R. Barlow Ed.). Society for Industrial and Applied Mathematics. Pennsylvania.
19. F. Gregory (1991) Causation and Soft Systems Models. Systemist. 13 (3), 105-112.