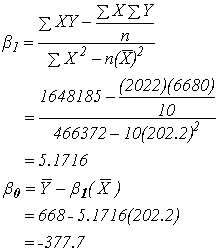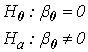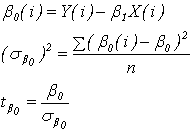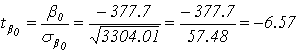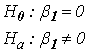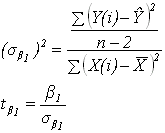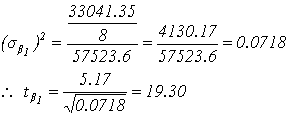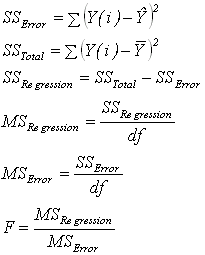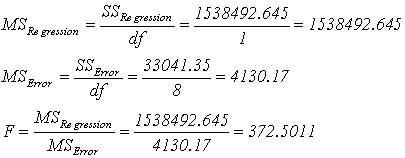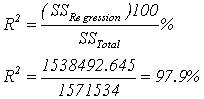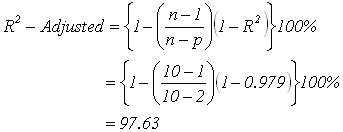|
ตัวอย่างการคำนวณ Simple Linear Regression Analysis ตัวอย่าง คณะนักวิจัยที่ทำการศึกษาเกี่ยวกับชีวิตของหมีป่าต้องการหาวิธีการจะประมาณค่าน้ำหนักของหมีที่อาศัยอยู่ตามธรรมชาติในป่า โดยมีจุดประสงค์ที่สำคัญคือในอนาคตข้างหน้านักวิจัยกลุ่มนี้ไม่ต้องการใช้เครื่องชั่งน้ำหนักในการทำการศึกษาเกี่ยวกับชีวิตหมีอีก ทั้งนี้เพราะมีความลำบากในการขนย้ายเหลือเกิน จึงทำการออกสำรวจกลุ่มตัวอย่างหมีป่า 10 ตัว หลากหลายขนาด ทั้งเพศผู้และเพศเมีย แล้วทำการชั่งน้ำหนักและวัดความยาวรอบอกบริเวณราวนมของหมีป่า ทั้ง 10 ตัว ได้ข้อมูลดังตารางต่อไปนี้
ตารางที่ 1. เมื่อมีตัวแปรต้นและตัวแปรตามเพียงอย่างละ 1 ตัวแปร สมการหรือ Model ที่ได้จะเป็นดังนี้
ขั้นตอนที่ 1 เตรียมข้อมูล X, Y จากตาราง ค่าที่เป็นตัวแปรต้นหรือ X คือความยาวเส้นรอบอก และค่าที่เป็นตัวแปรตามหรือ Y ก็คือค่าน้ำหนักนั่นเอง ซึ่งต้องเลือกให้ตรงด้วย หากท่านผู้อ่านสงสัยว่าเหตุใดผู้เขียนถึงเลือกแบบนี้ ที่จริงไม่ใช่เลือกครับแต่ความเป็นจริงต่างหาก วิธีสังเกตคือค่าที่เราจะหาหรือจะเป็นคำตอบในอนาคตคือตัวแปรตาม (Y) ส่วนค่าที่เราจะต้องใส่ในสมการ (Model) เพื่อให้เห็นคำตอบคือตัวแปรต้น ในโจทย์นี้ค่าที่จะเป็นคำตอบจากการใช้ Model คือค่าน้ำหนักนั่นเอง
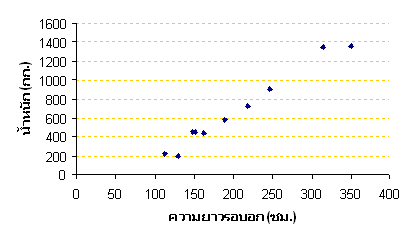
เมื่อเอาข้อมูล X,Y มาทำ Scatter plot พบว่าการเรียงตัวของจุดมีลักษณะเป็นเส้นตรง พอจะมองเห็นว่ามีความสัมพันธ์เป็นแบบเชิงเส้น และแนวของจุดชันขึ้นทำมุมกับแกน X มากพอประมาณ แสดงว่าค่าสัมประสิทธิ์ของตัวแปรต้นมากกว่า 0 หรือ Slope > 0 เข้าข่ายที่จะพิสูจน์ด้วย Regression analysis ได้ ขั้นตอนที่ 2 หาค่าผลรวม ค่าเฉลี่ย ผลคูณ ผลรวมของการคูณกันของตัวแปรต้นและตัวแปรตาม และค่ายกกำลังสองของตัวแปรต้น ท่านผู้อ่านต้องใช้โปรแกรม Excel ช่วยในการคำนวณ โดยคัดลอกข้อมูลจากตารางไปวางในตาราง Excel จากการคำนวณจะได้ค่าต่างๆดังตารางต่อไปนี้
ตารางที่ 2. ขั้นตอนที่ 3 คำนวณหาค่าคงที่และค่าสัมประสิทธิ์ของตัวแปรต้นในสมการ โดยนำค่าที่คำนวณได้จากตารางที่ 2 มาใส่ในสมการ ซึ่งสมการคำนวณดังกล่าวนี้ได้มีการคิดไว้แล้ว ผู้เขียนขอไม่พูดถึงที่มาของสมการในขั้นตอนนี้
ดังนั้น Regression model ที่ได้ คือ
หรือเขียนเป็นสมการความสัมพันธ์ตามข้อมูลจากตารางแรก คือ น้ำหนักหมี(โดยประมาณ) = -377.7 + 5.17 (ขนาดเส้นรอบวงบริเวณอก ซม. ) กก. ขั้นตอนที่ 4 ทดสอบสมมติฐานว่าค่าคงที่ (b0) และค่าสัมประสิทธิ์ (b1) ใน Model ที่คำนวณได้นั้นมีความจำเป็นต้องคงไว้ใน Model หรือไม่ ท่านผู้อ่านต้องนึกภาพตามนะครับว่าค่า b0 และ b1 ที่เรากำลังกล่าวถึงนี้เป็นตัวอย่างที่มาจากประชากรจำนวนหนึ่ง ซึ่งจะมีการกระจายรอบๆค่าๆหนึ่ง ซึ่งจริงๆแล้วค่าที่เราเห็นก็เป็นเพียงตัวอย่างหนึ่งที่ถูกดึงออกมาจากกลุ่ม ที่เราสนใจคือว่าค่าดังกล่าวนี้ เป็น 0 หรือไม่ ถึงเราจะเห็นค่าไม่เท่ากับ 0 แต่จริงๆค่าการกระจายกลุ่มนั้นอาจจะอยู่รอบๆ 0 ก็ได้ ถ้าเป็นเช่นนั้นถือว่าค่าดังกล่าวไม่มีนัยสำคัญของความต่างกับ 0 เราก็สามารถตัดค่า b0 หรือตัดพจน์ที่ b1 คูณอยู่ออกจาก Model ได้เลย โดยจะไม่ทำให้ค่า Y ที่ได้มีความแตกต่างกับเมื่อคงค่าดังกล่าวไว้ใน Model แต่อย่างใด และการกระจายของตัวของค่า b0 และ b1 นี้ก็เป็น Normal distribution ด้วย เหตุผลนี้เองที่เราต้องใช้ T-Test เพื่อทดสอบสมมติฐาน ว่ามีค่าเท่ากับ 0 หรือไม่ โดยสมมติฐานในการทดสอบ b0 คือ
การพิสูจน์สมมติฐานนั้นเราจะใช้ t-statistic โดยมีสมการดังนี้
จากสมการข้างบน เราจะเริ่มจากการหาค่า b0(i) และ sb0 เพื่อจะนำไปใช้หาค่า tb0 ในขั้นตอนสุดท้าย ผู้เขียนขอใช้ตาราง Excel ช่วยในการคำนวณ จาก Model ค่า b0 = -377.7 และ b1 = 5.17
ตารางที่ 3. จากตารางที่ 3 จะได้
เราจะปฏิเสธสมมติฐาน H0 : b0= 0 ถ้า
( a = 0.05 , df = n-2) จากตาราง T เราพบว่า t0.025,8 = 2.306 ซึ่งน้อยกว่า |tb0 | ที่คำนวณได้ ดังนั้นสมมติฐาน H0 : b0= 0 จึงไม่เป็นจริง นั่นคือค่า b0 มีค่ามากกว่า 0 อย่างมีนัยสำคัญ จึงต้องคงค่าไว้ใน Model สมมติฐานในการทดสอบ b1 คือ
การพิสูจน์สมมติฐานนั้นเราจะใช้ t-statistic โดยมีสมการดังนี้
เมื่อ
ตารางที่ 4. จากตารางที่ 4 จะได้
เราจะปฏิเสธสมมติฐาน H0 : b1= 0 ถ้า
( a = 0.05 , df = n-2) จากตาราง T เราพบว่า t0.025,8 = 2.306 ซึ่งน้อยกว่า |tb1 | ที่คำนวณได้ ดังนั้นสมมติฐาน H0 : b1= 0 จึงไม่เป็นจริง นั่นคือค่า b1 มีค่ามากกว่า 0 อย่างมีนัยสำคัญ จึงต้องคงพจน์ที่มี b1 เป็นสัมประสิทธิ์คูณอยู่ไว้ใน Model ไม่สามารถตัดทิ้งได้ นั่นคือ Regression model ยังคงเป็น
ขั้นตอนที่
5 การพิสูจน์ว่า Regression model
ที่ได้มานั้นเหมาะที่จะนำไปใช้คาดการณ์
( Predict ) ค่า Y ในอนคตมากน้อยเพียงใด
ซึ่งจะใช้วิธีพิสูจน์ค่าความคลาดเคลื่อน
(Error) ระหว่างค่า Y
ที่เก็บข้อมูลมาได้กับค่าที่ได้จากการใส่ค่า
X ใน Model ที่ได้มา ( H0 : Error จากการใช้ Model นี้ Predict ค่า Y เป็น Error ที่ไม่สามารถอธิบายได้เป็นส่วนใหญ่ Ha: Error จากการใช้ Model นี้ Predict ค่า Y เป็น Error ที่สามารถอธิบายได้เป็นส่วนใหญ่ สมการทางคณิตศาสตร์ที่ใช้ในการคำนวณ มีดังนี้
โดยที่ ่ SS : Sum Square หมายถึงค่าแต่ละค่ายกกำลังสองแล้วนำมาหาผลรวม MS : Mean Square หมายถึงค่าการเอาค่า SS มาหาค่าเฉลี่ยอีกโดยหารด้วย Degree of freedom.
ตารางที่ 5. จากตารางที่ 5 SSError = 33041.35 SSTotal = 1571534 ดังนั้น SSRegression = 1571534 - 33041.35 = 1538492.645 หาค่า Degree of freedom SSTotal : df = n -1 =10 -1 = 9 SSError : df = n -1-1 =10 -1 -1 = 8 >> มาจาก (dfTotal - 1 ) SSRegression : df = n -1 - 8 =10 -1-8 = 1 >> มาจาก (dfTotal - dfError ) ดังนั้น
เราจะปฏิเสธสมมติฐาน H0 ถ้า F > FCritical ( a = 0.05 , df >> n1=1, n2=8 ) จากตาราง F เราพบว่า F0.05,1,8 = 5.32 ซึ่งน้อยกว่า F ที่คำนวณได้ ดังนั้นสมมติฐาน H0 จึงไม่เป็นจริง นั่นคือ Error จากการใช้ Model นี้ Predict ค่า Y เป็น Error ที่สามารถอธิบายได้เป็นส่วนใหญ่ หมายความว่าความแตกต่างของค่า Y ที่เห็นส่วนใหญ่เกิดจากการใส่ค่า X ที่ต่างกัน ซึ่งเป็นสิ่งที่อธิบายได้ ส่วนเหตุอื่นๆที่มีผลทำให้เกิดความแตกต่างของค่า Y ในการใช้ Model นี้ มีน้อยมาก เราใช้ F -Statistics เพื่อรับรองว่า หากใช้ Regression model นี้ไปใช้ Predict ค่า Y แล้วจะให้ความคลาดเคลื่อนน้อย หรือพูดอีกอย่างคือมีความแม่นยำสูงนั่นเอง ขั้นตอนที่ 6 การหา Coefficient of Determination เป็นการคำนวณหาตัวชี้วัดว่า Model นี้สมควรจะได้รับการยอมรับมากน้อยเพียงใด ถึงแม้จะรับรองด้วย F-Statistics แล้วก็ตาม หลักการคือหาค่า Error จากการเปลี่ยนแปลงค่า X ซึ่งเป็นการเปลี่ยนแปลงที่เราจงใจ กับค่า Error รวมทั้งหมด ถ้าค่าที่ได้ใกล้เคียงกัน ก็ถือว่า ยอมรับได้ ถ้าน้อย ก็แสดงว่าค่า Error อื่นๆที่ไม่รู้ที่ไปที่มา มีปนอยู่มาก ถึงระดับหนึ่งอาจจะไม่สามารถยอมรับ Model นี้ได้เลย เราเรียกตัวชีวัดนี้ว่า R2 (อ่านว่า R - Square )
อาจจะเป็นไปได้ว่าเพราะความบังเอิญค่า R2 ที่คำนวณได้จึงสูง เราจะต้องทดสอบดูว่า ที่ค่า R2 สูงนั้นไม่ได้เป็นเรื่องบังเอิญ หลักการคือให้ทำการลด n ลง 1 ตัวแล้วหาค่า R2 อีกครั้ง หากยังสูงอยู่ก็ถือว่าไม่ได้เป็นเรื่องบังเอิญ แต่ถ้า R2 ใหม่นี้มีค่าต่ำกว่าค่าเดิมมาก แสดงว่าค่า R2 มีความไว (Sensitivity) ต่อการเปลี่ยนแปลง n มาก ควรจะต้องแก้ไข โดยอาจถึงขั้นต้องไปเก็บข้อมูลเพิ่ม เก็บข้อมูลใหม่ เลยทีเดียว เราเรียกว่า R2 -Adjusted
โดยที่ p คือจำนวนค่าคงที่และค่าสัมประสิทธิ์ของตัวแปรต้นใน Regression model (b0,b1,b2,....bn) ซึ่งในตัวอย่างนี้คือ 2 คือ b0,b1 นั่นเอง หากนำค่าที่ได้จากการคำนวณมาเขียนสรุปเป็นตารางจะได้ดังต่อไปนี้
ตารางที่ 6. ในกรณีที่เราใช้โปรแกรม Microsoft Excel ช่วยในการวิเคราะห์ จะได้ตารางออกมาดังต่อไปนี้
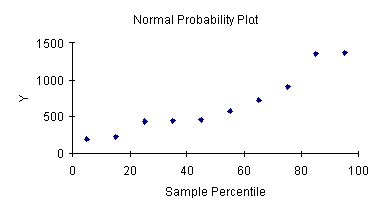
ตารางที่ 7. จะเห็นว่าถ้าเราใช้โปรแกรมช่วยวิเคราะห์ เราจะเห็นตารางค่าคงที่ ค่าสัมประสิทธิ์ของตัวแปรต้น และค่า T-Statistics (ตารางสีเทา) ซึ่งได้ค่า P-Value เป็น 0.00 แสดงว่าเราต้องปฎิเสธสมมติฐาน H0: ในขั้นตอนที่ 4 ทั้งกรณีสมมติฐานของค่า b0 และ b1 ในส่วนตาราง Anova (ตารางสีชมพู) ใช้เพื่อหาค่า F Statistics ได้ค่า P-Value เป็น 0.00 นั่นคือปฎิเสธสมมติฐาน H0 : ตามขั้นตอนที่ 5 เช่นกัน ในส่วนตาราง Regression statistics (ส่วนสีฟ้าอ่อน) ที่สรุปค่า Coefficient of Determination ที่ได้ตามขั้นตอนที่ 6 สุดท้ายเราสรุปว่าค่าที่คำนวณตามขั้นตอนที่ 1 ถึง 6 ได้ตรงกับค่าที่ได้จากการใช้โปรแกรม Micrsoft Excel ขั้นตอนที่ 7 การพิสูจน์คุณสมบัติ 3 ประการ เนื่องจากในการคำนวณด้วยมือตามขั้นตอนที่ 1-6 มีความยุ่งยากในการเตรียมข้อมูลในการแสดงกราฟ ผู้เขียนขอใช้กราฟที่ได้จากการวิเคราะห์ด้วยโปรแกรม Mocrosoft Excel - Normality
จากกราฟ การเรียงตัวของจุดค่า Y เทียบกับ Percentile เป็นแนว แม้จะไม่เป็นเส้นตรง โอกาสที่จะไม่เป็น Normal ค่อนข้างสูงทีเดียว แต่หากจะยอมรับว่าเข้าใกล้ Normal distribution ก็ไม่น่าเกลียดเกินไป - Independence
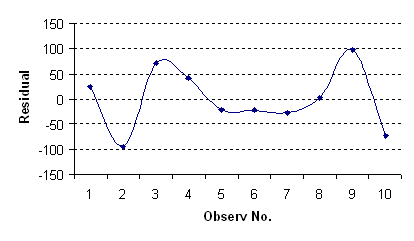
การทดสอบ Independence หรือความเป็นอิสระต่อกันของค่า X แต่ละค่าทำได้โดยการพล้อตค่า Residual เทียบกับหมายเลขของ X ที่เรากำหนดในตาราง จะพบว่า แนวของจุดถือได้ว่า ไม่มีทิศทางใดแน่นอน ไม่ได้อยู่ทางด้านลบหรือบวกอย่างเดียว ไม่ได้ขึ้นหรือลงอย่างเดียว ลักษณะเช่นนี้เราถือว่าความเป็นอิสระของ X แต่ละตัวอยู่ในเกณฑ์ที่ยอมรับได้ - Homoscedasticity
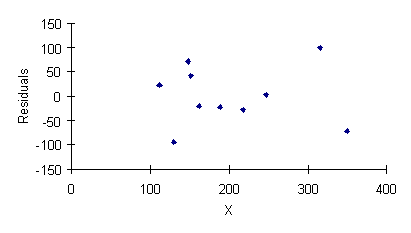
การทดสอบ Homoscedasticity มีวัตถุประสงค์คือ พิสูจน์ว่าค่าความคลาดเคลื่อนทุกๆย่านของค่า X ไม่ได้แตกต่างกันมากจนเกินไป โดยการพล้อต Residual กับค่า X (Fit) หากมีลักษณะอยู่ด้านบวก หรือลบตลอด เป็น 0 ตลอด กว้างออกตลอด เมื่อค่า X สูงขึ้น เราจะถือว่าไม่ผ่านเงื่อนไขนี้ จากกราฟเราพอจะอนุมานได้ว่า Residual ตลอดย่านค่า X ไม่ได้แตกต่างกันจนเกินเหตุ ดังนั้น เงื่อนไขที่สำคัญทั้ง 3 ก็ถือว่ายอมรับได้ เราจึงยอมรับว่า Regression model ที่ได้มานั้นสามารถเอาไปใช้ในการคาดการณ์ค่าน้ำหนักหมีป่าในอนาคต โดยจะได้คำตอบโดยประมาณที่ใกล้เคียงกับความเป็นจริงพอสมควร ซึ่งเพียงพอที่นักวิจัยจะใช้ค่าน้ำหนักที่คำนวณได้ไปใช้ในการพิสูจน์หรือวิเคราะห์อะไรก็ตามที่ต้องใช้ค่าน้ำหนักหมีมาเกี่ยวข้อง แล้วยังให้ข้อสรุปที่ถูกต้องยอมรับได้อยู่ เช่น ถ้าต่อไปนักวิจัยกลุ่มนี้ไปสำรวจหมีตัวที่ 11 พบว่ามีเส้นรอบอก 275 ซม. เมื่อใส่ค่าใน Regression model ก็จะได้ค่าน้ำหนักหมีประมาณ 1044 กก. อย่าลืมว่าคำตอบที่ได้ต้องเป็นค่าประมาณการณ์เท่านั้น ถึงแม้ขั้นตอนการวิเคราะห์ Regression จะดูยาวและต้องทำหลายอย่าง แต่เนื่องจากในปัจจุบันนี้ เรามีโอกาสใช้โปรแกรมคอมพิวเตอร์ช่วยในการวิเคราะห์ โดยที่เราไม่ต้องทำเอง ซึ่งก็จะได้ค่าเป็นตารางรายงานและกราฟออกมาให้เห็นเลย แต่ถ้าหากเราไม่เข้าใจว่าการวิเคราะห์หรือการคำนวณมีที่ไปที่มาอย่างไร ค่าที่เห็นในตารางที่คอมพิวเตอร์ให้มานั้น แต่ละค่ามาอย่างไร กราฟแต่กราฟหมายถึงอะไร และจะตีความอย่างไรดี ผู้เขียนก็ขอบอกว่าคอมพิวเตอร์ก็ช่วยไม่ได้ แต่เมื่อท่านผู้อ่านเข้าใจขั้นตอนวิเคราะห์ แต่ละค่าในตารางมีสมการในการคิดอย่างไรอยู่ กราฟแต่ละกราฟใช้ค่าอะไรพล้อต ใช้ดูอะไรแล้ว ก็จะสามารถอ่านและสรุปผลจากคอมพิวเตอร์ได้ถูกต้อง แม้แต่หากใส่ข้อมูลผิดก็ยังสามารถมองเห็นข้อผิดพลาดได้ คอมพิวเตอร์ก็มีความหมายเพียงเครื่องช่วยประมวลผลให้เราเท่านั้น
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||