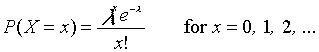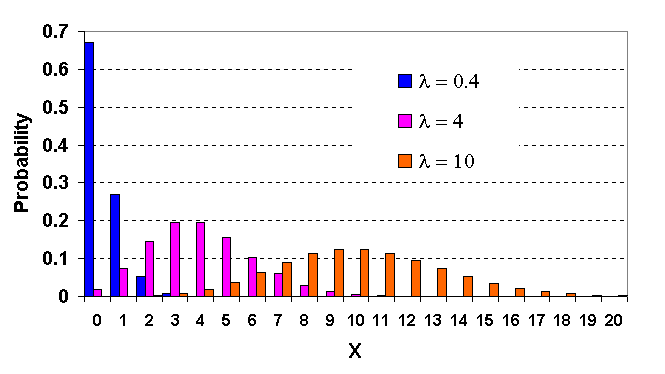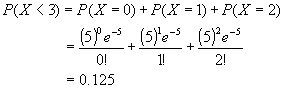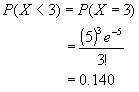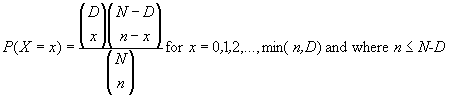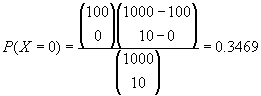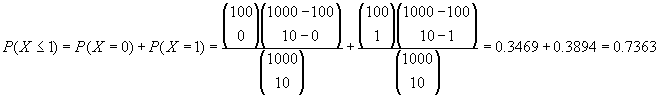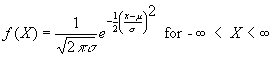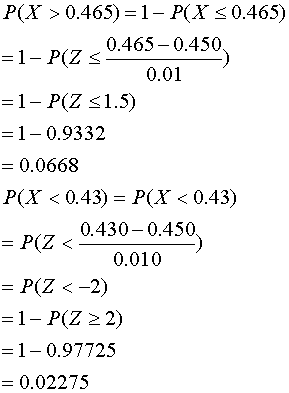รูปแบบการกระจายของค่าความน่าจะเป็น (Probability Distribution)

ความน่าจะเป็น (Probability) :  

ถือว่ามีความสำคัญเป็นอย่างยิ่ง เพราะจริงๆแล้วเราจะใช้วิชาสถิติในการคาดการเหตุการณ์ที่จะเกิดขึ้นในอนาคตหรือสิ่งที่จะเกิด ขึ้นกับประชากรส่วนมาก  โดยอาศัยข้อมูลที่เกิดขึ้นมาแล้ว  และเป็นเพียงตัวอย่างส่วนหนึ่งที่ถูกดึงออกมาจากประชากรส่วนมาก  มาเป็นพื้นฐาน  ดังนั้นเราจำเป็นต้องรู้ว่า เหตุการณ์แต่ละเหตุการณ์ มีโอกาสเกิด ขึ้นได้เท่าไหร่ ซึ่งเป็นคุณสมบัติตามธรรมชาติของสิ่งที่เรากำลังสนใจนั้น  เพราะถ้าเราไม่สามารถ รู้ว่าเหตุการณ์ที่เราสนใจ มีโอกาสเกิดขึ้นมากหรือน้อยน้อยเท่าไหร่ เราก็มิอาจที่จะคาดการณ์อนาคตหรือคาดการณ์ประชากรได้ถูกต้อง  นั่นแปลว่าเราก็ไม่สามารถใช้ วิชาสถิติเพื่อการนี้ได้เลย  ข้อมูลแต่ละประเภทก็จะมีลักษณะค่าโอกาสที่แตกต่างกัน และเมื่อเรานำค่าโอกาสมาแสดงในรูป กราฟ การกระจาย (Distribution) เราเรียกว่า การกระจายของค่าโอกาส (Probability Distribution) 

ตัวแปรสุ่ม ( Random Variable) :  

การสุ่ม (Randomization) ถือว่าเป็นสิ่งจำเป็นที่ผู้ที่เรียนรู้ ้เรื่อง โอกาส (Probability) จะต้องใช้และทำความเข้าใจเป็นอย่างยิ่งเช่นกัน   เครื่องมือทางสถิติจะหมดความหมายทันทีถ้าหากว่าการทำการทดลองใดๆ เพื่อให้ได้ข้อมูลมา ไม่ได้เกิดจากการสุ่มที่ถูกต้อง  นั่นแปลว่า โอกาสของเหตุการณ์ต่างๆที่ได้จากการทดลองไม่ได้เป็นไปตามธรรมชาติที่ควรจะเป็นของมัน (Bias) เพราะอย่าลืมว่า เราต้องการใช้วิชาสถิติเพื่อคาดการณ์เหตการณ์ที่จะเกิดขึ้นข้างหน้าหรือประชากร  หากโอกาสของเหตุการณ์ที่จะเกิดขึ้น ถูก Bias แล้ว วิชาสถิติก็ไร้ซึ่งประสิทธิผลทันที  เราก็ไม่จำเป็นต้องใช้วิชาสถิติ  ยกตัวอย่างให้เห็นได้อย่างชัดเจน ก็อย่างกรณีหวยล้อก  ที่กำลังโด่งดังในช่วงที่ผู้เขียนกำลังเขียนเนื้อหาส่วนนี้พอดี  อย่างรางวัลที่เลขท้ายสองตัว เลขที่มีโอกาสออก คือเป็นได้ตั้งแต่ 00 ถึง 99 โดยที่แต่ละตัวมีโอกาสออกได้เท่าเทียมกัน คือ 1 ใน 100 หรือ probability = 0.01 เวลาออกฉลากก็จะมีการหมุนวงล้อ ซึ่งในวิชาสถิติเรา เรียกว่าการทำการทดลอง (Experiment) เพื่อทำการสุ่มค่าให้เกิดค่า (Outcome) สมมุติมีการล้อค ให้ออก 33 ค่าแห่งโอกาสจะเปลี่ยนไปทันที โดยเลข 33 จะมี โอกาสเกิด 100 ใน 100 หรือ probabily = 1.00 ส่วนโอกาสเกิดเลขอื่นๆ ก็ไม่มี คือ 0 ใน 100 หรือ probability = 0.00 นั่นเอง ถ้าอย่างนี้ ไม่ต้องใช้วิชาสถิติให้ยุ่งยาก เพราะรู้อยู่แล้วว่าจะต้องออก 33 แน่นอนอยู่แล้ว

ในสถิติอนุมาน (Inferential Statistic) ทั้งโอกาส และ การสุ่ม ถือเป็นหัวใจหลัก  ในการสุ่มตัวอย่างออกมาจากประชากรจะต้องให้แต่ละตัวของสิ่งที่เราสนใจมีโอกาส ถูกเลือกมาเป็นตัวอย่างเท่าๆกัน  

• ค่าโอกาสการเกิด (Probability Value) คือค่าที่บ่งบอกโอกาสในการเกิดเหตุการณ์ต่างๆ เราใช้สัญญลักษณ์ คือ ( p )
• คำศัพท์ที่เกี่ยวข้อง

        - การทำการทดลอง (Experiment) คือการกระทำใดๆก็ตามที่มีจุดประสงค์เพื่อให้ได้ข้อมูล( Data )มา 

        - การทดลองแบบสุ่ม (Random Experiment) คือการกระทำใดๆที่ส่งผลให้ ตัวอย่างที่เราจะได้มานั้น มีโอกาสถูกเลือกเท่าๆกัน

        - ขอบเขตของเหตุการณ์ที่มีโอกาสเกิด (Sample Space) คือจำนวนค่าหรือจำนวนผลจากการทำการทดลอง ที่มีโอกาสเกิด

        - เหตุการณ์ที่เกิดขึ้น (Event) คือเหตุการณ์ที่เราได้จากการทำการทดลองแต่ละครั้ง ซึ่งก็คือสมาชิกแต่ละตัวใน เซ็ทของ Sample space นั่นเอง

ขอยกตัวอย่างเพื่อให้เห็นเป็นรูปธรรม เช่น  การทดลองทอดลูกเต๋า 1 ลูก  การโยนหรือทอดนั้นก็คือ Random Experiment ส่วนแต้มที่มีสิทธิ์เกิดหรือ Sample Space ก็คือ {1,2,3,4,5,6}  เมื่อโยนครั้งที่ 1 สมมุติแต้มที่ออกคือ 4 ซึ่งก็คือ Event นั่นเอง สมมุติว่าการทำการทดลองครั้งนี้โยนลูกเต๋าทั้งหมด 10 ครั้ง ได้ค่าเป็นดังนี้ 

                             { 4,2,4,1,3,6,3,5,6,2}

ค่าที่เราได้นี้ก็คือ Random Variable นั่นเอง

ชนิดของ Probability Distribution

นักสถิติได้ค้นพบ Probability Distribution หลากหลายชนิด แต่ที่เป็นที่คุ้นเคยและใช้งานบ่อยๆในงานอุตสาหกรรม หรือชีวิตประจำวันมากๆ พอจะแบ่งเป็นกลุ่มและชนิดย่อยๆ ได้ดังต่อไปนี้

• การกระจายที่เป็นข้อมูลไม่ต่อเนื่อง (Discrete Probability Distribution) ข้อมูลของการกระจายแบบนี้ต้องเป็นข้อมูลนับเท่านั้น  ตัวอย่างเช่น

                   - แบบมีรูปแบบแน่นอน ( Discrete Uniform Distribution)

                   - แบบมีสองสิ่งตัวอย่าง (Binomial Distribution)

                   - แบบพอยซองน์ (Poisson Distribution)

                    - แบบไฮเปอร์จีโอเมตริก (Hyper geometric Distribution)

• การกระจายที่เป็นข้อมูลแบบต่อเนื่อง (Continuous Probability Distribution) ตัวอย่างเช่น

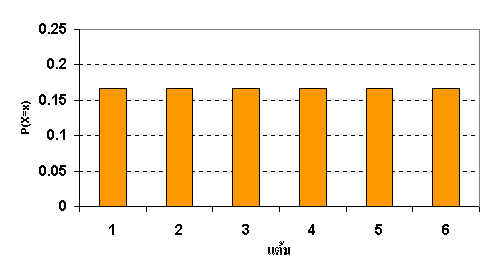
                   - แบบเอ็กซ์โปเนนเชียล (Exponential Distribution)

                   - แบบปกติ (Normal Distribution)

Discrete Uniform Distribution

สามารถเขียนเป็นสมการคณิตศาสตร์ ได้   P(X= x) = 1/n  แปลเป็นคำพูดก็คือ โอกาสที่จะได้แต้ม x เท่ากับ 1 ใน n

                 โดยที่              n    คือ    Sample Space 

                                     X   คือ    Random variable

                                     x    คือ    Event หรือค่าใดๆ ที่ได้

กราฟต่อไปนี้แสดงการกระจายของโอกาส (Probability Distribution) ของการโยนลูกเต๋า

Binomial Distribution

ข้อแตกต่างจาก Discrete Uniform Distribution คือ Binomial จะมีสิ่งตัวอย่างอยู่สองสิ่งปนกันอยู่  แล้วเราสนใจว่าเวลาเราเลือกตัวอย่างออกมาจะได้สิ่งตัวอย่างชนิดใด  ลักษณะโอกาสที่จะได้สิ่งตัวอย่างชนิดใด หรือโอกาสในการเกิดเหตุการณ์มีไม่เท่ากันขึ้นอยู่กับสัดส่วนของสองสิ่งที่เรากำลังดึง ตัวอย่างออกมา ตัวอย่างเช่น ในกล่องใบหนึ่งเราทราบว่ามีงานที่เรากำลังตรวจสอบอยู่ในกล่องจำนวน 1,000 ชิ้นแยกเป็นงานที่ดีจำนวน 800 ชิ้น และ งานที่มีตำหนิหรือ งานเสียอยู่ 200 ชิ้นคละเคล้ากันอยู่ ถ้าเราเก็บตัวอย่างออกมาจากกล่อง แปลว่าเรามีโอกาสหยิบได้ทั้งงานดีและงานเสีย เช่น หยิบตัวอย่าง มาแค่ 10 ตัวอย่าง นั่นแปลว่า เรามีโอกาสจับได้งานดีหมดทุกตัว หรือเจองานเสียปนมาด้วย 1,2,3 .... หรือเจองานเสียทุกตัวเลย  แต่โอกาสที่จะเจองาน เสียจำนวนมากก็ยิ่ง น้อยลงเรื่อยๆ โดยเฉพาะโอกาสที่จะเจองานเสียล้วนๆ 10 ตัวเลย ก็มีเหมือนกันแต่ก็น้อยที่สุด 

เช่นเดียวกันสมมุติว่าสัดส่วนของดีและของเสียที่อยู่ในกล่องเปลี่ยนไป เช่น ดี  950 เสีย 50 โอกาสที่จะเจอของเสียในการเก็บตัวอย่างก็จะลดลงไปอีก ในทาง กลับกัน หากแต่ละครั้งในการเก็บตัวอย่าง เราจับมา 20 ตัวอย่าง  โอกาสที่จะเจอของเสียในการเก็บตัวอย่างแต่ละรอบก็จะมีมากกว่าการเก็บคราวละ 10 ตัวอย่าง ดังนั้นปัจจัยหรือตัวแปร ทั้งสองนี้ส่งผลต่อโอกาสในการเจองานเสียที่เราสุ่มเก็บมาจากประชากร 

           - สัดส่วนของดี และของเสีย เราเขียนด้วย  p (Proportion) เช่น มีของดีอยู่ 800 ของเสียอยู่ 200 ค่า  p = 200/1000 หรือ p = 0.20 หรือมีของ เสียอยู่ 20 % นั่นเอง

           - จำนวนตัวอย่างที่เราเก็บมาในแต่ละครั้ง เช่น ครั้งละ 10 หรือ 20 เราแทนด้วย n

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้

                                                     โดยที่

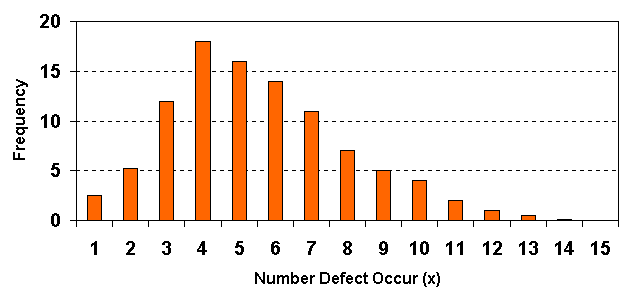
กราฟต่อไปนี้เป็นตัวอย่างของ Binomial distribution

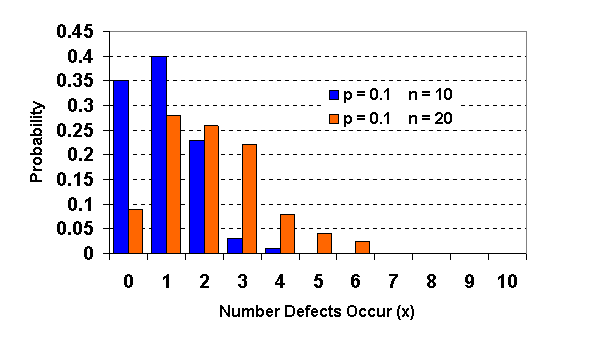
จากกราฟ เป็นผลมาจากการที่เราทำการสุ่มเก็บตัวอย่างครั้งละ 15 ตัวอย่าง และทำการเก็บครั้งละ 15 ตัวอย่างหลายๆครั้ง เรานำจำนวนงานเสียที่ได้แต่ครั้ง มาพล้อตเป็นกราฟแท่ง โดยแกน Y คือความถี่ที่พบค่านั้นๆ เราจะพบว่า เราจะพบงานเสียครั้งละ 4 ตัวมากที่สุด และค่ารอบๆ 4 ก็จะมากลดหลั่นลงมา

กราฟต่อไปนี้เปรียบเทียบให้เห็นผลของจำนวนตัวอย่างที่เราเก็บแต่ละครั้ง โดยที่สัดส่วนของของดีของเสีย ไม่เปลี่ยนแปลง

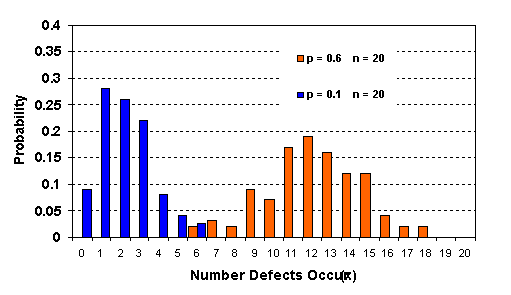
จากกราฟ เราจะเห็นว่าลักษณะ Probability distribution จะเปลี่ยนไปเมื่อเราเพิ่มหรือลดจำนวนตัวอย่างที่เก็บแต่ละครั้ง นั่นคือโอกาสที่จะพบของเสีย ก็เปลี่ยนแปลงไปนั่นเอง

กราฟต่อไปนี้เปรียบเทียบให้เห็นผลของสัดส่วนของของดีของเสีย โดยที่จำนวนตัวอย่างที่เราเก็บแต่ละครั้ง ไม่เปลี่ยนแปลง

จากกราฟ เราจะเห็นว่าลักษณะ Probability distribution จะเปลี่ยนไปเมื่อสัดส่วนของดีกับของเสียแตกต่างกัน นั่นคือโอกาสที่จะพบของเสีย ก็เปลี่ยนแปลงไปนั่นเอง

เราใช้ประโยชน์จาก Binomial Probability Distribution ได้อย่างไรบ้าง แน่นอนว่าในชีวิตจริงเราไม่จำเป็นต้องพล้อตกราฟ Distribution หรอก เราใช้ประโยชน์ ในการประมาณการค่าหรือจำนวนของเสีย หรือสิ่งที่เราสนใจ จากประชากรที่สองสิ่งปนกันอยู่ เช่น มีของดีของเสียปนกันอยู่ มีชื่อของชายและหญิงปนกัน เป็นต้น เราสามารถใช้สมการคณิตศาสตร์ข้างบนเพื่อหาค่าได้เลย แต่โดยทั่วไป โปรแกรมคอมพิวเตอร์ที่ออกแบบมาใช้กับงาน สถิติ จะมีส่วนให้เราใช้ในการหาค่าโอกาสที่เราจะพบสิ่งที่เราสนใจได้

ตัวอย่าง : จากข้อมูลที่ผ่านมาใน 4-5 สัปดาห์ เราพบว่าเครื่องจักรให้ Yield ในการผลิต 87 % วิศวกรมีการวางแผนเพื่อที่จะเก็บตัวอย่าง 10 ตัวอย่าง มาศึกษา อยากทราบว่าโอกาสที่จะไม่พบงานเสียเลย เป็นเท่าไหร่

จากโจทย์ เราจะได้  p = 0.13 และ n = 10 เมื่อนำค่าดังกล่าวป้อนเข้าสู่โปนแกรมคอมพิวเตอร์จะได้ผลลัพท์ดังนี้ 

< Computer Print out>

Probability Density Function

Binomial with n = 10 and p = 0.130000

x            P( X = x )

0.00          0.2484

คำตอบ คือ 0.2484 หรือ ถ้าเขาทำการทดลองหยิบตัวอย่างคราวละ 10 ตัวอย่าง 100 ครั้ง จะไม่เจองานเสียเลย 24.84 ครั้ง หรือเป็น 24.84% นั่นเอง โดยคำว่า Probability Density Function ( PDF ) นั้นหมายถึงโอกาสที่จะเจองานเสียนั่นเอง

ถ้าถามว่า โอกาสจะเจองานเสีย  4  ตัวเป็นเท่าไหร่ คำตอบก็คือ  2.6 ครั้งในการเก็บตัวอย่าง 100 ครั้ง

< Computer Print out>

Probability Density Function

Binomial with n = 10 and p = 0.130000

x                  P( X = x )

4.00               0.0260

ถ้าถามว่า โอกาสที่จะเจองานเสียไม่เกิน 4 ตัว เป็นเท่าใด  วิธีหาเป็นดังต่อไปนี้

            P(X<= 4)  =  P(X=0) + P(X=1) + P(X=2) + P(X=3) + P(X=4)

< Computer Print out>

Cumulative Distribution Function

Binomial with n = 10 and p = 0.130000

x                P( X <= x )

4.00              0.9947

คำตอบคือ 99.47 % จะเจองานเสียไม่เกิน 4 ตัว   คำว่า Cumulative Distribution Function ก็คือการหาผลรวมของค่าโอกาสตั้งแต่ x=0 ถึง ค่าที่เรากำหนด

Poisson Distribution

ปัจจัยที่ผลต่อลักษณะการกระจาย คือ อัตราการเกิดเหตุการณ์ที่เราสนใจโดยเฉลี่ย ต่อหน่วย สัญลักษณ์   l  เช่น การเกิดของทารกในตำบลที่ทำการศึกษา เรื่องประชากร โดยเฉลี่ย 16 คนต่อเดือน หรือ เครื่องจักรที่ใช้ผลิต เวลาผลิตงานจะเกิดงานเสียโดยเฉลี่ย 20 งานต่อชั่วโมง เป็นต้น นั่นหมายถึงมีโอกาสที่อัตราการเกิดของทารก อาจะมีมากหรือน้อยกว่า 16 คนต่อเดือน  หรือมีโอกาสจะเกิดงานเสียมากกว่าหรือน้อยกว่า 20 งานต่อชั่วโมงเหมือนกัน

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้

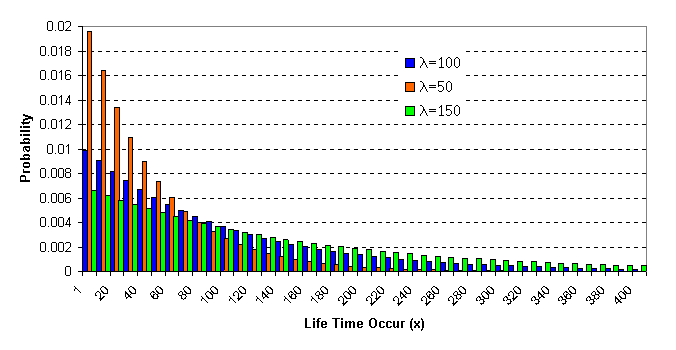
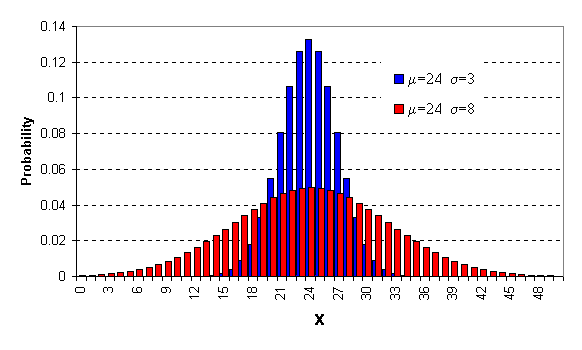
 ค่ากลาง การกระจาย และรูปร่าง การกระจายของ Poisson Distribution จะขึ้นอยู่กับ  l  กราฟต่อไปนี้ เปรียบเทียบให้เห็นความแตกต่าง

เช่นเดียวกับ Binomial Distribution เราสามารถหาอัตราการเกิดเหตุการณ์ที่เราสนใจ ต่อหน่วย ได้โดยที่เราไม่ต้องพล้อตกราฟ Distribution 

ตัวอย่าง : เครื่องจักรเครื่องหนึ่งที่ใช้ในการผลิตในสายการผลิต เกิด ปัญหาเครื่องหยุดทำงานโดยไม่ได้วางแผนก่อน โดยเฉลี่ยหลายเดือนที่ผ่านมาเป็น 5 ครั้ง ต่อสัปดาห์  อยากทราบว่า โอกาสที่เครื่องจักรจะหยุดทำงานน้อยกว่า 3 ครั้งต่อสัปดาห์เป็นเท่าใด  

ถ้าหาโดยใช้สมการ จะได้ดังนี้ 

< Computer Print out>

Probability Density Function

Poisson with mu = 5.00000

x           P( X = x )

0.00          0.006738

1.00          0.033690

2.00          0.084224

              รวม            0.124652

หรือ อีกวิธี

< Computer Print out>

Cumulative Distribution Function

Poisson with mu = 5.00000

x              P( X <= x )

2.00             0.1247

นั่นคืออัตราที่เครื่องจักรจะหยุดทำงานต่ำกว่า 3 ครั้งต่อสัปดาห์ คือ 12.465 %    

แต่ถ้า คำถามว่า โอกาสที่เครื่องจะหยุดทำงาน 3 ครั้งต่อสัปดาห์ เป็นเท่าใด หาได้จากสมการ

< Computer Print out>

Probability Density Function

Poisson with mu = 5.00000

x                  P( X = x )

3.00               0.1404

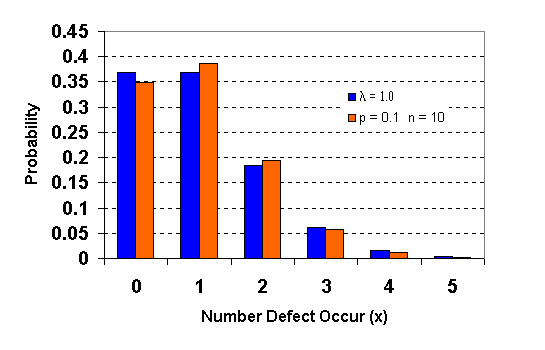
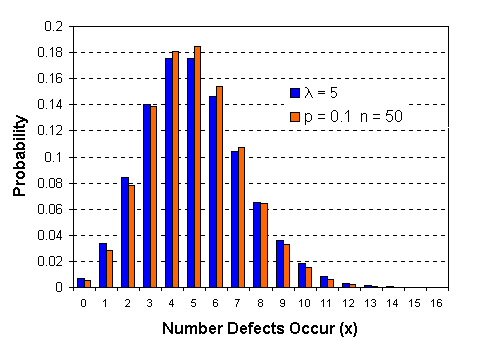
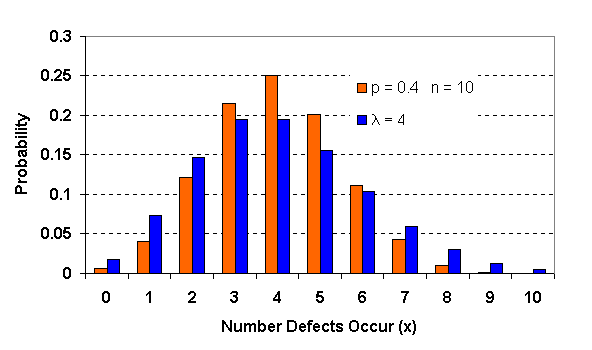
เราสามารถใช้ Poisson Distribution เพื่อประมาณ Binomial Distribution ได้ ถ้า  p<0.1 และ n มีจำนวนมากพอสมควร โดยเราจะทำการ หาค่าเฉลี่ยของเหตุการณ์ที่สนใจที่เกิดขึ้นได้จาก  l  =  np 

กราฟต่อไปนี้เป็นกราฟเปรียบเทียบระหว่าง Binomial และ Poisson Distribution 

จากรูปเปรียบเทียบระหว่าง  Binomial กับ Poisson Distribution จะเห็นว่าถ้า  p มากขึ้น ค่าโอกาสจะเริ่มแตกต่างกันมากขึ้น จนไม่สามารถใช้ Poisson เพื่อประมาณ Binomial ได้เลย

Hyper geometric Distribution

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้

หมายหตุ  :     

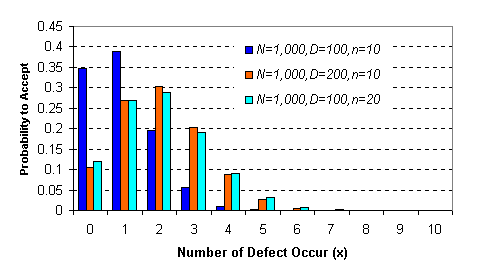
เช่น มีงานทั้งหมด 850 ชิ้น ในนี้มีงานเสียปนอยู่ 50 ชิ้น  ถ้าสุ่มตัวอย่างมา 2 ชิ้นผลที่ได้จะเป็นอย่างนี้

                โอกาสที่ทั้งสองชิ้นจะเป็นงานดี

                                  P(X=0)   =  (800/850)(799/849) = 0.886

                โอกาสจะเจองานเสียเพียงหนึ่ง จะมีกรณีตัวแรกเป็นงานดีตัวที่สองเป็นงานเสีย หรือกรณีตัวแรกเป็นงานเสียตัวที่สองเป็นงานดี ดังนั้น 

                                  P(X=1)  = (800/850)(50/849) + (50/850)/(800/849)  = 0.111

                  โอกาสที่จะเจองานเสียทั้งสองชิ้นเลย

                                   P(X=2) =  (50/850)(49)/849) = 0.003

ตัวอย่าง : โรงงานผลิตแห่งหนึ่งได้รับวัตถุดิบจาก Supplier มาเป็นจำนวน 1,000 ชิ้น  คำถามแรกก็คือว่าโรงงานจะรับหรือไม่ยอมรับ วัตถุดิบล้อตนี้ หรือก็คือ วัตถุดิบล้อตนี้ตรงกับข้อกำหนด (Specification) หรือไม่นั่นเอง แน่นอนหากจะมั่นใจ 100% จะต้องตรวจสอบงานทั้งหมด 1,000 ชิ้นนั้น ซึ่งแน่นอนว่า ไม่มี ใครทำ เพราะสิ้นเปลืองทั้งเวลา แรงงานคน และทรัพยากร อื่นๆ ซึ่งก็เป็นเหตุให้ค่าใช้จ่ายมากไปโดยไม่มีประโยชน์ ในทางปฏิบัต ิจึงเป็นเพียงแค่การสุ่ม ตัวอย่างมาทำการตรวจสอบเท่านั้น เช่น อาจจะดึงตัวอย่างมาแค่ 10 ชิ้นจาก 1,000 ชิ้นดังกล่าว โดยอาจจะกำหนดว่า จะรับวัตถุดิบล้อตนี้ ก็ต่อเมื่องาน ตัวอย่าง 10 ชิ้นนี้ ผ่านการตรวจสอบทั้งหมด โอกาสที่จะโรงงานผลิตนี้จะยอมรับวัตถุดิบล้อตนี้ เป็นเท่าไหร่ ถ้าหากในอดีตที่ผ่านมาวัตถุดิบชนิดเดียวกันนี้จาก Supplier เจ้านี้มีของเสียปนมาด้วยโดยเฉลี่ย 10%

จากโจทย์ เราจะพบว่า ถ้าสุ่มมาตรวจคราวละ 1 ตัว ถ้าไม่เจองานเสียก็จะหยิบตัวต่อไป โดยที่ไม่คืนตัวที่หยิบมาครั้งก่อนด้วย แต่ถ้าหยิบตัวถัดไปแล้วเจองานเสีย ก็หยุดได้ทันที เพราะถือว่าไม่ผ่านตามเงื่อนไขแล้ว

           X = ค่าของงานเสียที่เราตั้งเกณฑ์ไว้ จากโจทย์คือ 0 ชิ้น

           N = ขนาดของล้อต หรือของประชากร  จากโจทย์ คือ 1,000 ชิ้น

           D = ของเสียที่ปนอยู่กับของดี จากโจทย์คือ 100 ชิ้น (มาจาก 10%)

           n = จำนวนตัวอย่างในการเก็บ จากโจทย์คือ 10 

กราฟต่อไปนี้ เปรียบเทียบ 3 Hyper geometric Distribution

จากโจทย์ เราจะพบว่า เรามีโอกาสที่จะยอมรับวัตถุดิบจาก Supplier ถ้า N=1,000, D=100, n=10 เป็นดังน ี้

       - ถ้าเราตั้งข้อกำหนดว่า ต้องไม่พบ Defect จากตัวอย่างเลย จากกราฟจะได้ประมาณ 0.35 หรือประมาณ 35% เท่านั้น ถ้าจากคอมพิวเตอร์จะได้

< Computer Print out>

Probability Density Function

Hypergeometric with N = 1000, X = 100, and n = 10 

x               P( X = x )

0.00            0.3469

โดยหาได้จากสมการ

       - ถ้าเราตั้งข้อกำหนดว่า ต้องพบ Defect จากตัวอย่างไม่เกิน 1 ตัว  จากกราฟจะได้ประมาณ 0.35+0.39 หรือ  74%  ถ้าจากคอมพิวเตอร์จะได้

< Computer Print out>

Cumulative Distribution Function

Hypergeometric with N = 1000, X = 100, and n = 10

x                    P( X <= x )

1.00                 0.7363

โดยหาได้จากสมการ

Exponential Distribution

           - ศึกษาว่าหลอดไฟฟ้าใช้งานได้นานกี่ชั่วโมง

           - เวลาห่างระหว่างการชำรุดแต่ละครั้งของ เครื่องกำเนิดไฟฟ้า

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้ ถ้าต้องการหา ค่าโอกาสใดๆ (Probability Density Function , pdf)

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้ ถ้าต้องการหา ค่าโอกาสสะสม (Cumulative Distribution Function , cdf)

เมื่อ  l  คืออัตราการเกิดปัญหาโดยเฉลี่ย เหมือนกับ Poisson distribution โดยที่  l  จะเป็นตัวกำหนด ลักษณะของ Distribution  

ตัวอย่าง : โรงงานผลิตมอเตอร์ไฟฟ้าขนาดเล็กที่ใช้ในอุปกรณ์อิเล็กทรอนิกส์ แห่งหนึ่งได้ทำการเก็บตัวอย่างอายุการใช้งานของมอเตอร์ พบว่ามีลักษณะการ กระจายเป็นแบบ Exponential มีค่าเฉลี่ยอยู่ที่ 100 ชั่วโมง อยากทราบว่า โอกาสที่จะมีมอเตอร์ที่มีอายุการใช้งานไม่เกิน 60 ชั่วโมงเป็นเท่าใด

กราฟต่อไปนี้ เปรียบเทียบ ลักษณะของ 3 Exponential Distribution

จากโจทย์  l  = 100 ชั่วโมง   x = 60 

< Computer Print out>

Cumulative Distribution Function

Exponential with mean = 100.000

x              P( X <= x )

60.00          0.4512

ดังนั้นมอเตอร์ที่อายุการใช้งานไม่เกิน 60 ชั่วโมงจะมีประมาณ 45.12% ของจำนวนที่ผลิตได้ทั้งหมด

ถ้าถามว่า ที่มีอายุใช้งานประมาณ 60 ชั่วโมงจะเป็นเท่าไหร่  คำตอบคือ 0.55 %

< Computer Print out>

Probability Density Function

Exponential with mean = 100.000

x            f( x )

60.00        0.0055

Normal Distribution

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้ ถ้าต้องการหา ค่าโอกาสใดๆ (Probability Density Function , pdf)

• เราสามารถเขียนสมการคณิตศาสตร์ ของโอกาสได้ดังนี้ ถ้าต้องการหา ค่าโอกาสสะสม (Cumulative Distribution Function , cdf)

กราฟต่อไปนี้แสดงลักษณะการกระจายของ Normal Distribution  

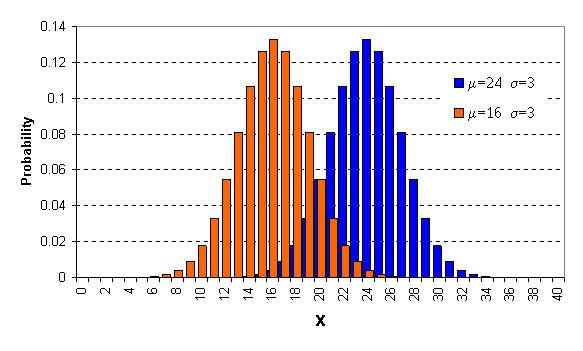
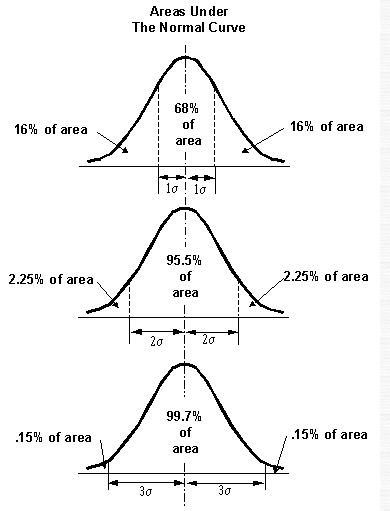
จากกราฟ จะเห็นว่า Parameter ที่สำคัญของ Normal distribution คือ ค่ากลาง ( m ) ซึ่งจะเป็นตัวกำหนดตำแหน่งหรือ Location และค่า เบี่ยงเบนมาตรฐาน (s) ซึ่งเป็นตัวกำหนด ความลาดหรือ ขนาดของการกระจาย จึงสามารถเขียนสัญลักษณ์ได้ดังนี้

X~N(m,s²) 

มีความหมายว่าค่า X มีการกระจาย ตัวแบบ Normal distribution โดยค่ากลางคือ m และมีการกระจายหรือ Variance คือ s² 

คุณสมบัติที่สำคัญของ Normal distribution มีดังนี้

      1.  ค่าโอกาส หรือความถี่สูงที่สุดมีค่าเดียว (One mode)

      2.  ค่าเฉลี่ยของประชากร หรือข้อมูลทั้งหมด อยู่ตรงกลางของโค้งการกระจายพอดี

      3. ค่าที่อยู่มากกว่าและน้อยกว่าค่ากลางจะมีค่าลดลงเรื่อยๆ ในลักษณะสมมาตร (Symmetry) ทำให้ Mean ,Median และ Mode คือค่าเดียวกัน 

      4. ปลายทั้งสองข้างจะเข้าหาแกน X แต่จะไม่มีที่สิ้นสุดและไม่มีโอกาสแตะกับแกน X ได้เลย

      5. สามารถใช้เพียงค่าเฉลี่ย (Mean) กับค่าเบี่ยงเบนมาตรฐาน (Standard Deviation) ในการอธิบายได้

พี้นที่ใต้กราฟการกระจายแบบ Normal distribution ทั้งหมดจะมีค่าเท่ากับ 1.00 หรือ 100% แต่ค่าพื้นที่ใต้กราฟแต่ละส่วนหาได้ดังนี้

Standard Normal Distribution

โดย ที่ค่าแปลงมาแล้วนี้เราเรียกว่า Z-Score ดังนั้น บางครั้งเราก็เรียกการกระจายใหม่นี้ว่า Z-Distribution โดยมีสมการคณิตศาสตร์ดังนี้

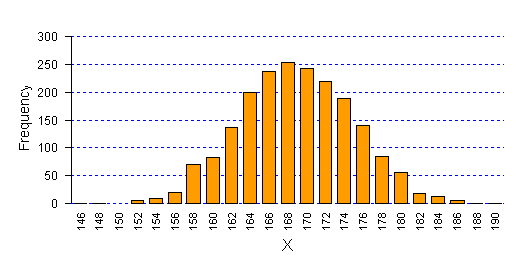
กราฟต่อไปนี้ เปรียบเทียบ การกระจายของข้อมูล ส่วนสูงของผู้ชายไทยอายุ 17-30 ปีจากการสุ่มตัวอย่างจำนวน 2,000 คน

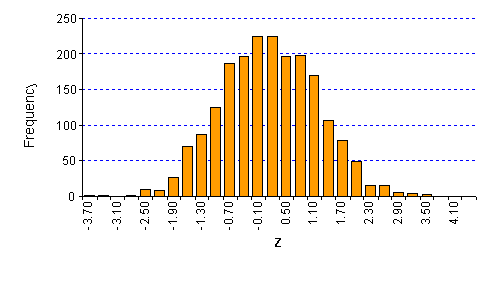
เมื่อทำการแปลงเป็น Z-score แล้ว จะเห็นว่าลักษณะการกระจายของข้อมูลยังคงเหมือนกับ X-score อยู่ แต่ค่ากลางจะอยู่ที่ 0 และมีค่าเบี่ยงเบน มาตรฐานอยู่ที่ 1 โดยค่า Z จะมีทั้งมากว่า และน้อยกว่า 0

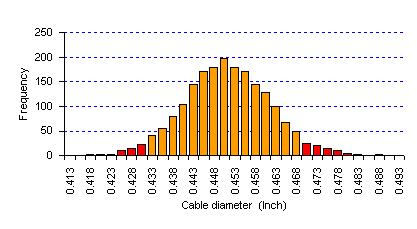
การประยุกต์ใช้ Normal Distribution และ Standard Normal Distribution

ตัวอย่าง : โรงงานผลิตเคเบิ้ลใยแก้วกำหนด Specification ไว้ว่าค่ากลางของเส้นผ่าศูนย์กลางของเคเบิ้ลต้องเท่ากับ 0.450 นิ้ว และต้องอยู่ในย่าน 0.430 นิ้ว ถึง 0.465 นิ้ว  โดยตัวอย่างที่เก็บได้มีลักษณะการกระจายเป็นแบบ Normal มี สมการเป็น   X~N(0.450,0.010) อยากทราบว่ามีเคเบิ้ลที่ไม่ตรง ตามข้อกำหนดเท่าไหร่

จากโจทย์ เราจะต้องหาพื้นที่ใต้กราฟ จาก P(X>0.465) + P(X<0.43) ซึ่งเราจะต้องแปลงข้อมูลจาก Inch ให้เป็น Z ก่อน

ดังนั้นจำนวนเคเบิ้ลใยแก้วที่ Diameter ไม่ตรงข้อกำหนด เท่ากับ   0.0668 + 0.02275  = 0.08955 หรือเท่ากับ 8.955%

จะเห็นว่าการหาพื้นที่ใต้กราฟ จะต้องแปลงข้อมูลให้เป็นค่า Z-Score ก่อน แล้วนำค่า Z-Score ดังกล่าวไปเปิดตาราง Z-Table เพื่อให้ได้ค่าพื้นที่ ใต้กราฟมา  แต่สามารถคำนวณได้จากโปรแกรมคอมพิวเตอร์ เป็นดังนี้

< Computer Print out>

Cumulative Distribution Function

Normal with mean = 0 and standard deviation = 1.00000

 x               P( X <= x )

-2.0000            0.0228

-1.5000            0.0668

เนื่องจากโปรแกรมคอมพิวเตอร์ (Minitab) ถูกโปรแกรมให้หาค่าพื้นที่ด้านซ้ายมือของค่าที่กำหนดเสมอ  ดังนั้นเมื่อต้องการหาค่าพื้นที่  Z = 2 จึงใส่ค่าในเครื่องเป็น  Z = -2  ซึ่งให้ค่าพื้นที่ด้านซ้าย ของ  Z = -2  แต่พื้นที่นี้จะเท่ากันกับพื้นที่ด้านขวามือของ Z = 2  เหมือนกัน เพราะ หลัก Symmetry ของ Normal distribution