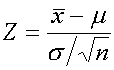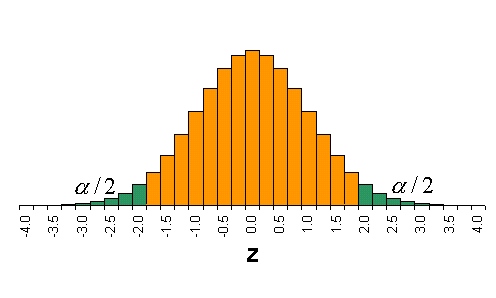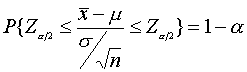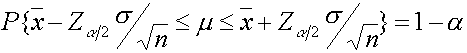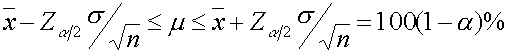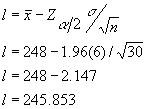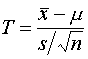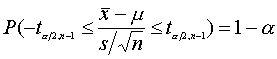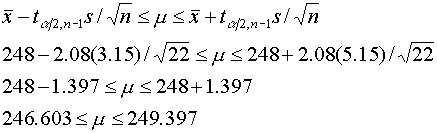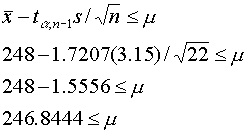ทฤษฎีช่วงความเชื่อมั่น ( Confidence Interval Theorem)

ืการที่เราทำการเก็บตัวอย่างมาจำนวนหนึ่งแล้วหาค่าเฉลี่ย เพื่อนำมาประมาณค่ากลางของประชากร ( m ) เช่น. เมื่อเก็บตัวอย่างปริมาณบรรจุนม UHT จำนวน 25 กระป๋องได้ค่าเฉลี่ยเท่ากับ 248 cc ทั้งที่ข้อกำหนดระบุว่านมแต่ละกระป๋องต้องบรรจุ 250 cc หากเราใช้วิธีประมาณประชากรแบบ Point Estimation เราก็จะสรุปว่า ปริมาณบรรจุนมที่กำลังทำการเก็บข้อมูลอยู่นี้ ไม่ได้ตรงตามข้อกำหนด แล้วจะทำยังไงถึงจะบอกได้ว่าจริงๆแล้วปริมาณบรรจุของนม ในแต่ละกระป๋องที่กำลังผลิตอยู่นะ ยังเท่ากับ 250 cc หรือไม่หากเราเปลี่ยนมาใช้วิธีประมาณประชากรแบบช่วง (Interval estimation) ผลสรุปอาจจะบอกว่าปริมาณบรรจุนม จากการสุ่มตัวอย่างครั้งนี้ยังเท่ากับ 250 cc อยู่

ช่วงความเชื่อมั่นกรณีรู้ค่าความแปรปรวน ( Confidence Interval on the Mean : Variance known)

แนวคิดพื้นฐานของ Confidence interval

เมื่อ  l  คือ lower limit และ  u  คือ upper limit  ซึ่งราเรียกว่า " Two-sided confidence interval " เราสามารถบอกได้ว่าโอกาสที่ค่ากลางของประชากรจะอยู่ภายใน limit จะหาได้จากสมการ

ในกรณีนี้  a คือ Error risk หรือ ค่าที่บ่งบอก ความเสี่ยงที่เราจะ พยากรณ์ค่า m ผิดพลาด  ดังนั้น ถ้าเราพูดถึงค่าความเชื่อมั่น เราก็ต้องไม่ลืม ค่าความเสี่ยง ด้วยเหมือนกัน ดั้งนั้น   100(1-a) % คือ เปอร์เซนต์ความเชื่อมั่น ที่เรากำลังสนใจ

นอกจากนั้นก็ยังมี " One-sided confidence interval " ซึ่งมีสมการดังต่อไปนี้

จากสมการข้างบนนี้ เราเรียกว่า lower-confidence interval  โดยที่  l  คือค่า lower limit 

จากสมการข้างบนนี้ เราเรียกว่า upper-confidence interval  โดยที่  u  คือค่า upper limit 

ดังนั้น ค่า 100(1- a )%   จึงเรียกว่า ค่าความเชื่อมั่น ของ พารามิเตอร์  m   เมื่อเราอ้างอิงทฤษฎี Sampling distribution for mean ที่มีค่ากลางคือ m และค่าการกระจายเท่ากับ  s²/n  ดังนั้น

 ซึ่งเป็น Standard normal distribution ดังรูป

เมื่อการกระจายเป็นแบบ Normal  ได้ว่าค่า a จึงต้องหารสอง ในกรณีที่หา Two-sided confidence interval  จากรูปจะได้ว่า

เมื่อแทนค่า Z จะได้ว่า

จัดรูปแบบสมการใหม่จะได้ว่า

โดยที่

             X   : ค่าเฉลี่ยของตัวอย่างที่ทำการเก็บตัวอย่างแบบสุ่มมาจากประชากร

             n :  จำนวนตัวอย่าง

ในกรณีนี้เรารู้ค่า Variance ของประชากร  เพราะเราระบุค่า s ได้  ดังนั้น ค่าเปอร์เซนต์ความเชื่อมั่นของค่า m หาได้จากสมการ

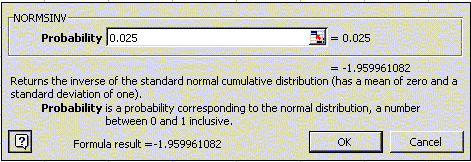
ตัวอย่าง  เมื่อวิศวกรได้ทำการสุ่มเก็บตัวอย่างกระป๋องนม UHT มา 30 กระป๋อง เพื่อตรวจสอบปริมาณบรรจุนมแต่ละกระป๋อง พบว่าค่าเฉลี่ยอยู่ที่ 248 มิลลิลิตร โดยที่ข้อกำหนดบอกว่า ขนาดบรรจุนมทุกกระป๋องจะต้องเท่ากับ 250 มิลลิลิตร และที่ผ่านมา พบว่าค่า เบี่ยงเบนมาตรฐาน (s) อยู่ที่ 6 มิลลิลิตร  จงหาช่วงความเชื่อมั่น ที่ 95% ของขนาดบรรจุนม UHT นี้

จากโจทย์  เราจะได้ว่า   1- a  = 0.95   นั่นคือ    a = 0.05  เพราะฉะนั้น ค่า Z _a/2=Z_0.025   ซึ่งเมื่อคำนวนหาค่า Z โดยใช้ โปรแกรม Minitab จะได้ดังนี้

Inverse Cumulative Distribution Function

Normal with mean = 0 and standard deviation = 1.00000

P( X <= x )           x

0.0250             -1.9600

โดยจะให้ค่าด้านลบ แต่เนื่องจากกฏของ Normal distribution เราจึงได้ค่าด้านบวก โดยเพียงแต่กลับเครื่องหมายเท่านั้นเอง 

หรือหากใช้ ฟังก์ชันคณิตศาสตร์ของ MS Excel เราจะได้ค่าดังนี้

เพียงแต่ วิธีการประมวลผลทางคณิตศาสตร์จะแตกต่างกัน คือ MS Excel จะให้เราใส่ค่า 1- (a/2)  แต่จะให้ผลเหมือนกัน คือค่า Z ณ a/2

ดังนั้นเราสามารถหาค่า Lower-confidence limit ได้จาก

เพราะฉะนั้น  Upper-confidence limit  = 248+2.147 = 250.147

ดังนั้น 95% ความเชื่อมั่น ของค่าปริมาณบรรจุนม UHT ทุกกระป๋องจะอยู่ระหว่าง 245.853 ถึง 250.147 มิลลิลิตร  หรือแปลว่า 95% ของนม UHT ที่ผลิตออกมานั้น จะมีค่าบรรจุน้ำนมในกระป๋อง อยู่ระหว่าง   245.853 ถึง 250.147 มิลลิลิตร ซึ่งอีก 5% จะเป็นค่าที่ต่ำและสูงกว่า ช่วงความเชื่อมั่นดังกล่าว ในจำนวนใกล้เคียงกัน คือมากกว่าก็ ประมาณ 2.5% และน้อยกว่าก็ประมาณ 2.5%

ช่วงความเชื่อมั่นกรณีไม่รู้ค่าความแปรปรวน ( Confidence Interval on the Mean : Variance unknown)

เพราะว่าสิ่งที่เราจะไม่รู้เลย ก็คือค่าพารามิเตอร์ ของประชากร  เราจึงจำเป็นต้องศึกษาผ่านการเก็บตัวอย่าง เพราะฉะนั้นเราจึงต้องอ้างอิง หัวข้อ t-distribution โดยคิดที่ degree of freedom  n-1 ดังนั้น เราสามารถหา Confidence interval ได้จาก

จากสมการ two-sided confidence interval

แทนค่า T ในสมการ เช่นเดียวกับกรณี Z จะได้

จัดรูปแบบสมการใหม่จะได้ว่า

ดังนั้น ค่าเปอร์เซ็นต์ความเชื่อมั่นของค่า m หาได้จากสมการ

ตัวอย่าง เก็บค่าบรรจุน้ำนมกระป๋อง UHT มา 22 กระป๋อง ได้ค่าเฉลี่ย X = 248 มิลลิลิตร และค่า s = 3.15 มิลลิลิตร  ค่าความเชื่อมั่น 95% ของค่าเฉลี่ยของประชากร จะอยู่ในช่วงใด

จากโจทย์  เราจะได้ว่า   1- a  = 0.95   นั่นคือ    a = 0.05  เพราะฉะนั้น ค่า t _a/2= t_0.025  และ ค่า n-1 = 21  ซึ่งเมื่อคำนวณหาค่า t โดยใช้ โปรแกรม Minitab จะได้ดังนี้

Inverse Cumulative Distribution Function

Student's t distribution with 21 DF

P( X <= x )         x

0.0250            -2.0796

 เพราะฉะนั้น  ค่า t_0.025 ที่ degree of freedom =21 คือ   2.080 

เราสามารถหา Confidence interval ได้ดังนี้

นั่นแปลว่า ปริมาณบรรจุนม UHT ที่ผลิตขณะนี้ 95% จะมีค่าอยู่ระหว่าง 246.603 ถึง 249.397 มิลลิลิตร ส่วนที่เหลืออีก 5% นั้น จะมากและน้อยกว่า ช่วงดังกล่าวในจำนวนเท่าๆกัน คือ 2.5% จากข้อกำหนดที่บอกว่าปริมาณบรรจุนมในแต่ละกระป๋องจะต้อง 250 มิลลิลิตร เราสามารถสรุปได้ว่า นม UHT  ล้อตนี้ ปริมาณบรรจุต่ำกว่าเกณฑ์ กำหนดด้วยความเชื่อมั่นว่า คำสรุปนี้ถูกต้อง 95%

ในบางครั้งเราอาจจะต้องการทราบเพียงแค่ Limit ด้านเดียว หรือเราต้องการรู้  Confidence interval เพียวด้านเดียว   จากโจทย์เดียวกันนี้เราสามารถ หา Lower confidence limit ได้  โดยที่เราจะต้องหา t _a ที่  degree of freedom 21  เมื่อใช้ โปรแกรม Minitab ในการหาค่า t จะได้ดังนี้

Inverse Cumulative Distribution Function

Student's t distribution with 21 DF

P( X <= x )        x

0.0500           -1.7207

จะได้ว่า t  จะ มีค่า 1.7207   ดังนั้น Lower confidence interval หาได้จาก

จาก Confidence interval ที่ได้ เราตีความว่า 95% ของนมที่ผลิตได้ ล้อตนี้ มีปริมาณบรรจุ แต่ละกระป๋อง ตั้งแต่ 246.8444 มิลลิลิตร ขึ้นไป ส่วนอีก 5% นั้น น้อยกว่า 248.8444 มิลลิลิตร

หัวข้อเรื่อง Confidence interval นี้ จะใช้เยอะมากในหัว การทดสอบสมมติฐาน ดังนั้น จึงจำเป็นที่ผู้อ่านจะต้องทำความเข้าใจ  และที่สำคัญ เนื้อหาในเรื่อง Confidence interval เองก็มีมากมายหลายเรื่อง แต่ผู้เขียนเห็นว่า เรื่องที่ได้เขียนมานี้ เป็นเรื่องพื้นฐาน และมีการใช้เยอะที่สุด