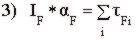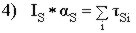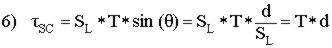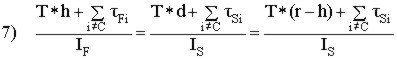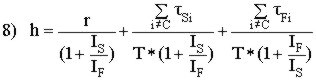|
|
|
�
Kenneth M. Sasaki 2001, Todos los derechos reservados.
1) Conceptos
Importantes. Lee
esta secci�n si: Quieres
verificar por ti mismo la validez de las principales afirmaciones de la teor�a
del An�lisis de trayectorias y entender algunos de los an�lisis del quinto cap�tulo
"Teor�as err�neas y Marketing enga�oso". Recomendamos
que al menos os le�is el apartado de "Cuadros de Referencia" ya que
va a resultar muy �til para comprender las siguientes secciones. Este
cap�tulo tiene una dificultad elevada. S�ltate
esta secci�n (menos la secci�n "Cuadros de Referencia") si: Aceptas
las afirmaciones que realizamos acerca del An�lisis de Trayectorias y simplemente
te interesa utilizar el An�lisis de Trayectorias para sacar conclusiones acerca
de c�mo funciona una suspensi�n y hacer comparaciones entre distintos modelos.
El
entendimiento completo del An�lisis de Trayectorias requiere conocer algunos
conceptos. Recomendamos a todos aquellos que deseen conocer completamente este
m�todo que dediquen el tiempo necesario para familiarizarse con estos conceptos
ya que la mayor�a de las teor�as incorrectas lo son por ignorar o malinterpretar
algunos de estos conceptos, sobre todo el de Centro de Masas. A)
Sistema de Referencia. Antes
de analizar una situaci�n debemos de elegir un Sistema de Referencia. Normalmente
lo representaremos mediante un sistema de ejes coordenados en el espacio, consistente
en dos ejes perpendiculares que se cruzan en el origen. Normalmente llamaremos
a estos ejes Eje X y Eje Y. Dependiendo de la informaci�n que queramos dar utilizaremos
un sistema de coordenadas de dos (En un plano) o de tres coordenadas. Es
habitual se�alar las unidades en estos ejes, de esta forma cualquier punto del
espacio estar� definido por su coordenadas, que en el caso del plano, por ejemplo,
ser�n una pareja de n�meros. Este sistema de referencia se conoce como Sistema
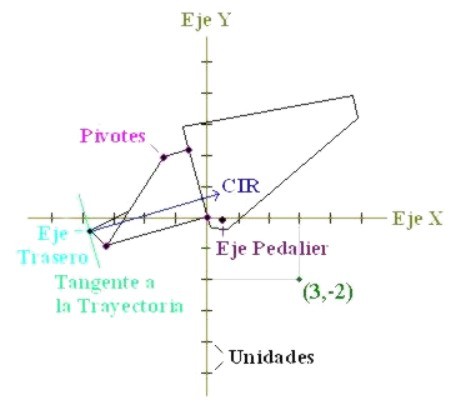
de Coordenadas Cartesianas. La
figura 2.1 muestra un sistema de coordenadas de dos dimensiones. Los ejes aparecen
en un color dorado, las unidades de longitud (En este ejemplo no se ha especificado
la escala, pero normalmente si se hace.) est�n marcadas en negro. En el cuadrante
inferior derecho hemos colocado un punto (3,-2) como ejemplo, la coordenada
X suele colocarse primero. Un cuadro est� colocado en este diagrama y se ha
hecho coincidir el pivote principal con el origen de coordenadas. Figura
2.1 El
sistema de referencia debe de estar definido por objetos fijos como la tierra
o en todo caso el cuadro de la bicicleta. El sistema de referencia hay que considerarlo
como si estuviese unido a un objeto. Si ese objeto est� sufriendo una aceleraci�n
lineal o angular (Si estuviese rotando) el sistema de referencia tambi�n lo
est�, en estos casos diremos que es un Sistema de Referencia No Inercial. Si
el sistema de coordenadas de la figura 2.1 estuviese fijado a la tierra, con
el tiempo, en cuadro de la bicicleta se ir�a moviendo respecto al origen. Como
la tierra solo sufre peque�as aceleraciones podemos considerarla como un Sistema
de Referencia Inercial. Si el sistema de coordenadas estuviese unido al triangulo
delantero de la bicicleta, entonces definir�amos la posici�n de los componentes
que forman parte de la suspensi�n respecto al triangulo delantero. Como el triangulo
delantero sufre constantes aceleraci�n habr�a que considerarlo como un Sistema
de Referencia No Inercial. Una
cosa que hay que considerar en los sistemas de referencia no inerciales es que
pueden aparecer fuerzas externas y momentos debido a la aceleraci�n del sistema.
La mas conocida es la fuerza centr�fuga. Si ponemos el ejemplo de las atracciones
de feria que est�n constantemente girando, uno siente que existe una fuerza
(como la gravedad) que nos aleja del del centro de rotaci�n, esa es la fuerza
centrifuga, y en este caso es solo aparente. No
debemos confundir la fuerza centrifuga con la fuerza centr�peta, esta �ltima
es la que nos desv�a de seguir en l�nea recta, oblig�ndonos a girar. La fuerza
centr�peta si es una fuerza real. A
veces lo �nico importante es definir un punto de referencia en el objeto, sin
indicar cual es el origen ni cual es la escala de longitudes. En este caso,
definimos el sistema de referencia nombrando un objeto pero sin necesidad de
dar mas detalles. Por ejemplo, debemos establecer el Sistema de referencia del
triangulo delantero. Esto se hace cuando queremos considerar el movimiento de
los objetos respecto al objeto al que hemos fijado el sistema de referencia,
pero sin dar importancia a los detalles. B)
Grados de
libertad. Un
objeto tiene un grado de libertad cuando puede moverse o girar en una sola direcci�n.
Un cuerpo totalmente libre tiene seis grados de libertad, es decir, puede moverse
en las tres direcciones coordenadas y girar en esas mismas direcciones. El
An�lisis de trayectorias se apoya en las limitaciones de los grados de libertad
que tienen los componentes de una bicicleta. Por ejemplo, si el sistema de referencia
es el suelo, el cuadro de una bicicleta que circule en l�nea recta tiene tres
grados de libertad, puede moverse horizontalmente, verticalmente y girar en
el plano de la rueda. Si fij�semos el triangulo delantero en el espacio, el
resto de los componentes tendr�an como mucho un grado de libertad. C) Cambios
en la naturaleza. Las
ecuaciones (Tambi�n llamadas funciones) que describen las leyes de la naturaleza
son continuas. Esto quiere decir que el valor de una variable no dar� un salto
si la otra va variando de una forma continua. El
resultado es que, si imaginamos la posici�n de un pivote y su barra correspondiente
movi�ndose de forma suave, las ecuaciones de movimiento tambi�n cambiar�n de
forma suave. El movimiento no puede pegar un salgo de golpe, el comportamiento
del mecanismo se comporta de forma continua. D) Aproximaci�n. Una
de las cosas mas dif�ciles que tiene que aprender un estudiante es a hacer aproximaciones.
La forma mas simple de aproximaci�n es aquella en la que tenemos una cantidad
mucho mas grande que otra. Vamos a poner dos ejemplos con masas para decir cual
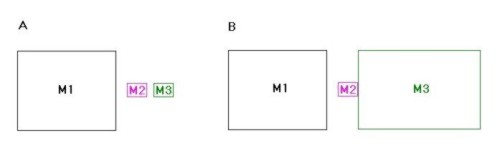
el la manera correcta de hacer la aproximaci�n. Consideremos
una masa M1 que es mucho, mucho mas grande que otras dos masas M2 y M3 en la
figura 2.2 A. Estas masas pueden moverse sin que exista fricci�n en una direcci�n,
si consideramos el movimiento de todos los cuerpos no podemos aproximar M2 y
M3 a cero porque entonces perderiamos una informaci�n importante. Por otra parte
es posible aproximar M1 con infinito y seguir obteniendo resultados. (Esto suele
hacerse cuando estudiamos la interacci�n de objetos peque�os y la tierra). En
la figura 2.2 B tenemos la situaci�n opuesta de la 2.2 A, en este caso podemos
ignorar a la masa M2 cuando estamos estudiamos la interacci�n entre M1 y las
otras dos. Estos
dos ejemplos demuestran que, en algunas situaciones, un elemento inusual puede
ser aproximado. Figura
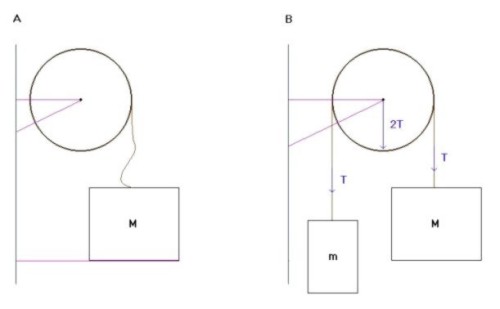
2.2 Fij�monos
ahora la figura 2.3 A, tenemos un bloque M conectado con un cuerda a una polea
de masa mucho mas peque�a que la de M que adem�s gira sin fricci�n sobre su
eje. Si queremos conocer que sucede cuando dejamos caer el bloque no podemos
obviar la masa de la polea ya que sino el resultado no ser�a exacto. En
la figura 2.3 B sin embargo, si las masas de M y m
son muy superiores a las de la polea, podemos ignorar la masa de �sta
y conseguir un resultado v�lido. Encontraremos
mas informaci�n sobre este tema en el apartado "Aproximaci�n de la masa"
del tercer cap�tulo. Figura
2.3 E) Centro
de Masas (CM). El
CM de un s�lido, o un sistema de s�lidos, es un punto tal que el momento de
la resultante (Suma de todas las masas) desde un punto O es igual al la suma
de los momentos de las distintas masas respecto a ese punto. El
CM de un objeto sim�trico, por ejemplo, est� en el eje de simetr�a. El CM de
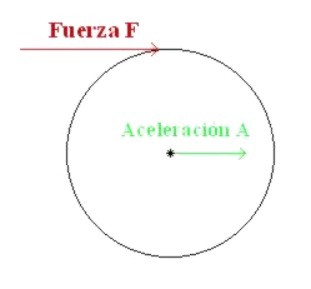
una rueda est� en el eje de la rueda. Para
nosotros, el aspecto mas importante de este concepto es que una fuerza aplicada
sobre un cuerpo produce una aceleraci�n en el Centro de Masas paralela a dicha
la fuerza. Por ejemplo, una fuerza aplicada sobre una rueda en un punto cualquiera
de su circunferencia (en el plano de la rueda) causar� una aceleraci�n en el
eje paralela a esa fuerza. Si la rueda esta libre, comenzar� a moverse en esa
direcci�n y tambi�n a girar. La figura 2.4 ilustra esta situaci�n. Figura
2.4 Para
ver la aplicaci�n que tiene este fen�meno vamos a comentar un experimento al
que hemos llamado "El Basculante y la Rueda": Un
basculante (Igual al que pueda tener una bicicleta, por ejemplo) est� anclado
al suelo mediante una articulaci�n en la que no existe fricci�n. Al otro extremo
del basculante hay una rueda De masa M que tambi�n puede girar sin fricci�n
sobre su eje. Una cuerda de masa despreciable est� sujeta al la circunferencia
exterior de la rueda y su extremo libre est� apuntando hacia abajo en el lado
derecho de la rueda. En el momento inicial todo el conjunto est� en equilibrio,
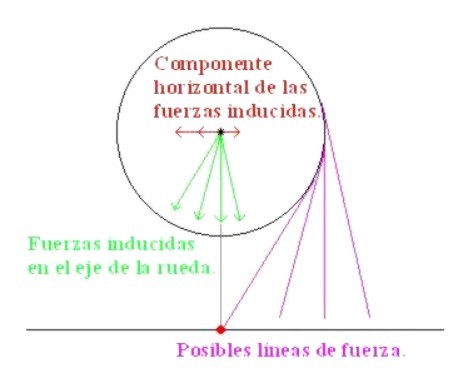
con el basculante colocado en posici�n vertical. Pregunta:
�En que direcci�n debemos de tirar de la cuerda para que el sistema siga en
posici�n vertical? Respuesta:
Debemos de tirar de forma vertical y hacia abajo. Si
tiramos hacia abajo y a la izquierda la rueda caer� hacia el lado izquierdo,
si tiramos hacia la derecha la rueda caer� hacia el lado derecho. Si tiramos
en la direcci�n del pivote, la rueda caer� hacia la izquierda. La figura 2.5
ilustra esta situaci�n. Figura
2.5 El
truco est� en darse cuenta de que la fuerza de la cuerda se transmite al eje
de forma paralela y para que el basculante siga en equilibrio la componente
horizontal debe de ser cero. Este
ejemplo es muy similar a lo que sucede en una bicicleta con un dise�o monopivote
en el que la tierra ha sustituido al triangulo delantero. Nota:
A muchas personas les cuesta aceptar el resultado de este ejercicio, incluso
a los profesores de F�sica les cuesta entenderlo a la primera, y hasta ahora
los dise�adores de bicicletas lo han ignorado. En cualquier caso, este concepto
es esencial para entender la interacci�n de las fuerzas que genera el pedaleo
y la suspensi�n de una bicicleta. Si
el lector quiere comprobar este experimento por si mismo puede realizarlo con
un portabicicletas de la marca Yakima o similar (que har� de basculante) y una
rueda de bicicleta. Si se aplica una fuerza intentando que pase por el eje (es
lo mas com�n) la rueda caer� hacia un lado. Si la fuerza se aplica verticalmente
la rueda girar�, pero se mantendr� en equilibrio. Esta
explicaci�n tambien puede encontrarse en el libro "Classical Dynamics of
Particles and Systems" de Marinon, fecha de edici�n 1970, p�ginas 67 y
68. En
el ejemplo anterior hemos aplicado solo una fuerza a la rueda, en el que la
inercia contraresta la fuerza exterior. Debemos de considerar caso en los que
se aplican mas de una fuerza en la rueda. Si existen dos o mas fuerzas actuando
sobre la rueda, creando dos momentos opuestos entre s� en el eje y la masa de
la rueda es peque�a comparada con las otras cantidades, podemos ignorar la masa
de la rueda. El ejemplo mas sencillo es el que aparecia en la figura 2.3 B. Mientra
el mecanismo est� en marcha la tensi�n T en cada lado de la rueda es la misma
(Siempre que despreciemos el peso de la rueda) y la fuerza en el eje es 2T.
En este caso las dos fuerzas son paralelas pero si no lo fuesen, la fuerza que
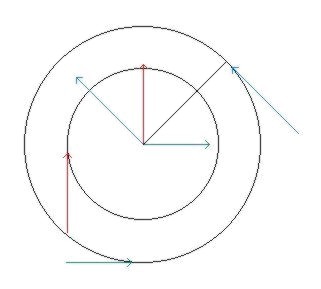
act�a sobre el eje ser�a la suma de los vectores. La
figura 2.6 muestra las fuerzas actuando en el eje de una rueda, de masa despreciable,
sometida a dos fuerzas con diferentes direcciones. Figura
2.6 Mas
adelante, en la figura 2.12 de la secci�n "Una mirada intuitiva sobre las
fuerzas y los momentos" aparecer� un ejemplo de este tipo, en el que bielas
y platos son la rueda de este ejemplo, y la fuerza del ciclista y la de la cadena
son las dos fuerzas externas. Aquellos que quieran entender la figura 2.12 deber�an
de tener en mente la figura 2.6. F) Condici�n
coaxial. Si
una rueda o una biela est� montada de forma coaxial con el pivote de un mecanismo,
no importar� como se halla conseguido esta configuraci�n. En una bicicleta,
la rueda trasera puede estar unida a las v�inas o a los tirantes y en el caso
del pedalier, �ste puede estar en el triangulo delantero o en el trasero pero
esto no tendr� importancia siempre que los objetos de los que hablamos est�n
montados de forma coaxial. G)
Centro Instant�neo de Rotaci�n. Imagina
un mecanismo que tiene dos componentes r�gidos (Entre otras cosas). Dos barras
r�gidas unidas al resto de los componentes mediante pivotes, luego conecta estos
dos elementos entre s�. Un ejemplo de este mecanismo es una suspensi�n trasera
del tipo paralelogramo deformable con Horst Link. En este caso un componente
ser�n los tirantes y el otro el tri�ngulo delantero. Lo
siguiente es elegir un sistema de referencia que colocaremos en el triangulo
delantero. Ahora podemos calcular la tangente de la trayectoria del eje trasero
calculando el Centro Instant�neo de Rotaci�n (CIR). Esto lo haremos dibujando
dos l�neas que unan los puntos de pivote de las dos barras del sistema. Si las
barras son lineales (No suele ser as�), los ejes determinar�n nuestras l�neas.
El punto donde se cruzan las dos l�neas es el CIR. La tangente a la trayectoria,
en un momento dado, de cualquier punto que se encuentre en esa barra (Tirantes)
ser� perpendicular a la l�nea que una ese punto con el CIR.
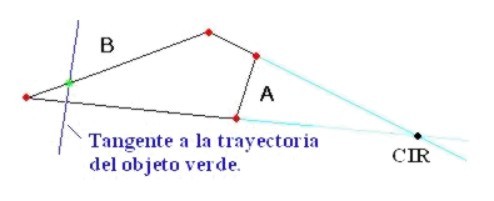
La
figura 2.7 nos muestra un sistema de cuatro barras, los puntos rojos representan
a los pivotes, y las l�neas de color celeste son las que unen los pivotes inferiores
y superiores. El punto negro en el que se intersectan las dos l�neas celestes
es el Centro de Rotaci�n Instant�neo (CIR) de todos los puntos que se encuentran
en la barra B (Tirantes), el sistema de referencia se encuentra fijado a la
barra A (Triangulo delantero). El punto verde representa el eje de la rueda
trasera y la l�nea azul, que representa la tangente a la trayectoria del eje
trasero cuando se mueve respecto a la barra A. Esta l�nea es perpendicular a
la l�nea que une el punto verde y el negro. Figura
2.7 La
idea es que para un �ngulo peque�o dq,
los movimientos de las dos barras (Vainas y bieletas) producen el mismo movimiento
en dicho punto (Eje de la rueda) que el que producir�a si rotase alrededor del
CIR. ���ADVERTENCIA!!!
El CIR no es un pivote "Virtual", en general, est� siempre en movimiento,
a diferencia de un pivote. En la figura 2.7 la barra A se mueve respecto a la
barra B y el CIR est� constantemente en movimiento, como tambi�n lo est� la
l�nea azul que representa la tangente a la trayectoria del eje trasero. Muchas
teor�as acerca de las suspensiones en las bicicletas se han debido a atribuir
al CIR las mismas propiedades que a un pivote. El CIR nos aporta una buena informaci�n,
pero s�lo para un momento en el tiempo, de ah� su nombre Centro INSTANT�NEO
de Rotaci�n. Un pivote se podr�a decir que es un Centro Constante de Rotaci�n. La
figura 2.8 muestra un cuadro con un sistema de suspensi�n de 4 Barras. Las l�neas
azules marcan varias posiciones del CIR del triangulo trasero en relaci�n con
el delantero. La l�nea roja representa la trayectoria del CIR a medida que la
suspensi�n se comprime. Si la distancia desde el eje de la rueda trasera y un
punto fijo en el espacio es pr�cticamente constante se puede decir que la trayectoria
del eje trasero es pr�cticamente circular. En ese caso podr�amos decir que ese
pivote virtual ser�a distinto para cada punto de la barra. En algunos casos
no existir� este punto de pivote virtual ya que para que la aproximaci�n que
estamos haciendo sea v�lida las desviaciones deben de ser peque�as.
punto en el espacio es el "Pivote Virtual" del eje trasero.
En la figura 2.8 las l�neas verdes nos revelan que existe un punto de pivote
virtual para este tipo de dise�o. Hay que observar que este punto de pivote
virtual solo funciona para el eje trasero. El c�lculo del CIR si es v�lido para
todos los puntos de la barra que corresponde a los tirantes de la bicicleta,
pero el punto de Figura
2.8 2) Una
mirada intuitiva sobre las fuerzas y los momentos. Lee
esta secci�n si: Si quieres ver
un an�lisis semi-cualitativo de las fuerzas y momentos de inercia que act�an
en el funcionamiento de una suspensi�n trasera. Entender esta secci�n al completo
no es importante para poder entender despu�s el an�lisis de trayectorias. Esto
es s�lo para gente que quiera profundizar un poco mas. Esta secci�n es
la mas dif�cil de entender de todo el trabajo. Lee
s�lo las conclusiones (en negrita) de este apartado si: Solo quieres conocer
las conclusiones del an�lisis para aplicarlas en otras secciones. Las conclusiones
no son demasiado dificiles de entender por eso os recomendamos que intent�is
leerlas, aunque s�lo sea por encima. Si no entend�is algo no hay que darle importancia
y lo que se consiga aprender siempre vendr� bien. S�ltate
esta secci�n si: Simplemente
te interesa utilizar el An�lisis de Trayectorias para sacar conclusiones acerca
de c�mo funciona una suspensi�n y hacer comparaciones entre distintos modelos. En este
apartado vamos a realizar un estudio intuitivo de las fuerzas y los momentos
de inercia en una bicicleta con un sistema de suspensi�n trasera de tipo monopivote
para entender algunos aspectos que cualquier teor�a sobre dise�o de suspensiones
debe de tener en cuenta. Esto ayudar� a entender que ocurre en una bicicleta
de doble suspensi�n y que limitaciones hay que aceptar en un dise�o que se considere
viable. Hemos intentado usar lo menos posible los c�lculos matem�ticos pero
hemos utilizado algunos para demostrar algunas soluciones y principios.
Aquellos sin una base t�cnica pueden ignorar los c�lculos y mirar directamente
las Conclusiones, escritas en letra negrita. La lecci�n
mas importante que debemos sacar de esta secci�n es que la distribuci�n de masas
es una consideraci�n importante en el aspecto f�sico y cient�fico de una suspensi�n.
Ninguna teor�a cuantitativa puede ser correcta si no toma en cuenta esta consideraci�n. La pr�ctica
com�n nos dice que la suspensi�n ideal no debe de moverse debido al pedaleo,
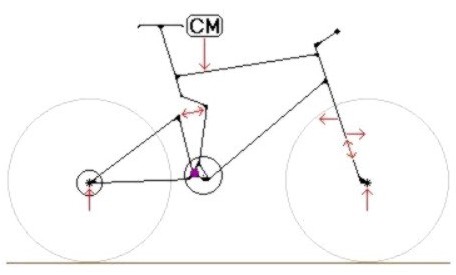
nosotros seguiremos esta pr�ctica. La figura 2.9
muestra una bicicleta del tipo monopivote en una situaci�n de "no pedaleo"
con varias fuerzas actuando sobre ella. Hemos despreciado el rozamiento en los
bujes y el del aire. El s�mbolo "CM" representa la situaci�n aproximada
del centro de masas del conjunto Ciclista+Triangulo Delantero. Figura
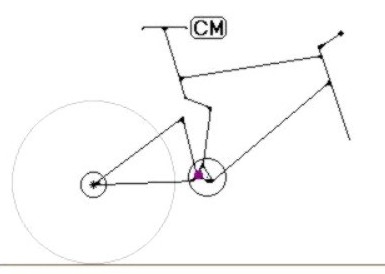
2.9 Todas
las fuerzas suman cero cuando no hay pedaleo. Por esta raz�n s�lo examinaremos
las fuerzas y momentos resultantes de la acci�n de una pedalada. La figura 2.10
representa la figura sin las fuerzas relacionadas con la situaci�n de "no
pedaleo". Figura
2.10 1)
I*a
= �
t. Aqu�,
I es el momento de inercia del cuerpo en cuesti�n, a
es la aceleraci�n
angular y �
t
es la suma
de todos los momentos del cuerpo. Este es el equivalente angular de m a
= �
F.
Usando la ecuaci�n 1) vamos a examinar todos los aspectos que intervienen para
poder conseguir que la suma de los momentos en el pivote sea lo mas pr�xima
a cero que sea posible. Para
conseguir unos c�lculos precisos, este m�todo no ser� demasiado �til. Esto se
debe a que no se pueden conocer exactamente los valores de algunos momentos
y adem�s su valor var�a en funci�n del tiempo (salvo el de la tensi�n de la
cadena, que depende de la posici�n de las bielas). Solo alcanzaremos parcialmente
la complejidad de un an�lisis completamente riguroso. Pero
para nuestro estudio, que ser� b�sicamente intuitivo, este m�todo va a ser muy
�til ya que podremos usarlo para explorar una serie de cuestiones con uso reducido
de los c�lculos. Vamos
a empezar con un comentario sobre la fuerza de la cadena. Uno
debe de ser muy cuidadoso cuando pensamos en l�neas de fuerza en las que la
magnitud, la direcci�n y la posici�n son muy importantes. Incluso las combinaciones
de plato y pi��n equivalentes producen l�neas de fuerza que difieren en magnitud,
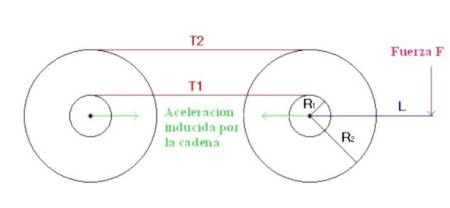
direcci�n y posici�n. La
figura 2.11 muestra una transmisi�n con dos posibilidades con la misma relaci�n,
la relaci�n es 1:1. L es el brazo de palanca de la biela, R1 y R2 son los radios
de cada pi��n y T1 y T2 son las tensiones de la cadena para cada caso. Figura
2.11 Si
aplicamos una fuerza F a L, creamos una tensi�n en la cadena (Lo hacemos con
un caso cada vez). El resultado de la ecuaci�n de momentos para la biela es
el siguiente: 2)
I*a = F*L - T1*r = F*L - T2*R De esta manera, T1/R = T2/r. Lo
que quiere decir que la tensi�n de la cadena decrece a medida que aumentamos
el radio de platos y pi�ones � Un resultado interesante. Como acabamos de
ver, dos situaciones con la misma relaci�n 1:1 no producen la misma interferencia
entre la suspensi�n y el pedaleo. Esto no deber�a de sorprendrernos ya que la
energ�a transmitida a trav�s del sistema es la misma en ambos casos. La energ�a
se puede expresar como T*d,
donde T es la tensi�n de la cadena y d el la longitud de la cadena. Como la
longitud de cadena que movemos en una revoluci�n es mayor cuando el plato es
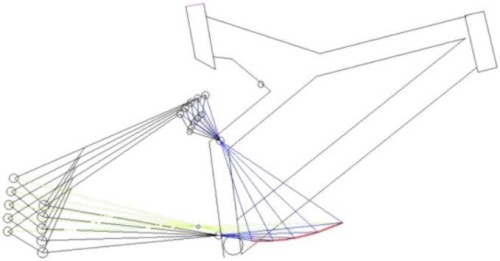
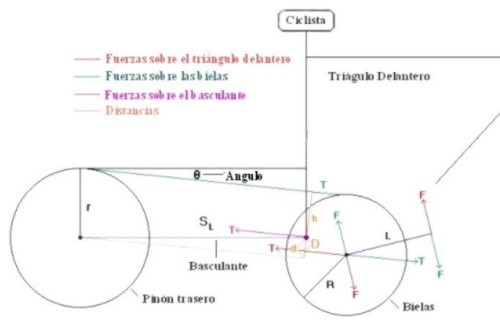
mayor, la tensi�n debe de ser menor para que el final la energ�a sea constante. Continuemos,
la figura 2.12 muestra el diagrama de los pr�ximos c�lculos. El tri�ngulo que
aparece incompleto representa el tri�ngulo delantero de la bicicleta y en el
se encuentra el eje de pedalier y por lo tanto las bielas. La l�nea horizontal
inferior representa un basculante de longitud SL. "R" es
el radio del plato y "r" el del pi��n. "L" es la longitud
de la biela y "F" la fuerza que ejerce el ciclista. "T"
es la tensi�n resultante, "h" es la distancia perpendicular entre
la cadena y el pivote. "D" es la distancia perpendicular entre el
pivote y la fuerza que genera la tensi�n de la cadena en el eje de pedalier
y "d" es la distancia perpendicular entre el pivote y la paralela
a la l�nea de tensi�n que pasa por el eje trasero. q
es el �ngulo entre la l�nea de la cadena y el basculante. Recordemos
ahora el fen�meno del centro de masas que aparec�a explicado en la figura 2.6
de la secci�n "Centro de masas". Este fen�meno se aplica tanto a la
fuerza que act�a en la biela como a la de la tensi�n de la cadena y su resultado
se aplica en el eje de pedalier. No
hemos dibujado todas las fuerzas presentes en los dos miembros, solo aparecen
aquellas relacionadas o producidas por las fuerzas del pedaleo. Hemos
asumido que el eje de pedalier y el pivote est�n pr�ximos entre s� comparando
con la dimensi�n del triangulo delantero, esto nos permitir� aproximar las fuerzas
en el pivote provenientes de las bielas como si los dos fuesen coaxiales. Tambi�n
asumimos que el peso de la biela es nulo. Esto nos permitir� adecuar las fuerzas
en el plato y en la biela y poder aplicarlas en el eje de pedalier. Figura
2.12 En los
siguientes c�lculos, el sistema de referencia para la ecuaci�n de momentos del
triangulo delantero est� centrado con la posici�n del pivote principal, y no
girar� con respecto a la tierra. El sistema de referencia para la ecuaci�n de
momentos est� centrada en el eje de la rueda trasera y tampoco puede girar.
Como ninguno de los dos sistemas de referencia puede girar, los cuerpos mantendr�n
el �ngulo que hay entre ellos si sus aceleraciones angulares son iguales (La
aceleraci�n angular inicial es cero). IF y IS son, respectivamente,
los momentos de inercia del triangulo delantero respecto al pivote principal
y el momento de inercia del basculante respecto al eje trasero. tFi
y tSi
representan una serie de momentos de los respectivos cuerpos respecto a su origen
de coordenadas, entre los que se incluyen los momentos producidos por las fuerzas
de la cadena, horquilla y rueda delantera (Fricci�n e Inercia), la aceleraci�n
de la bicicleta, la rotaci�n de las bielas y de las piernas del ciclista y tambi�n
los momentos producidos por las interacciones entre los dos miembros de la suspensi�n
(En el Ap�ndice A) "Algunos c�lculos suplementarios sobre la teor�a del
pivote en la l�nea de la cadena" Se realizan algunos c�lculos suplementarios
a los que aparecen aqu�). {Un
apunte: No debe de preocuparnos demasiado el siguiente detalle pero un lector
astuto observar� que estamos usando dos sistemas de referencia no-inerciales
para cada parte del cuadro. En estos sistemas de referencia la aceleraci�n de
la bicicleta y los momentos que interaccionan son en este caso momentos ficticios.} Las
ecuaciones de momentos para el conjunto Ciclista/Triangulo delantero y para
el basculante son las siguientes: Conseguir
el objetivo de minimizar el movimiento de la suspensi�n provocado por la fuerza
sobre el pedal suele implicar la b�squeda de la mejor posici�n para el pivote
principal en relaci�n con las fuerzas de la cadena en una situaci�n (Distribuci�n
de masas, etc.) concreta. Para hacer esto debemos de expresar la tensi�n de
la cadena en t�rminos de "h" y resolver para esta cantidad en la ecuaci�n
correspondiente. Afortunadamente, los momentos de la cadena y de la biela son
f�ciles de introducir en la ecuaci�n y nos permitir�n una formula que relaciona
la posici�n del pivote y de la cadena. tFC
representa el momento en
el triangulo principal de las fuerzas de la cadena resultantes de la fuerza
sobre el pedal. Se
observa que para un biela de masa despreciable, F = T*R/L,
El momento en el triangulo principal debido a la fuerza sobre el pedal y la
tensi�n resultante de la cadena es. 5)
tFC
= F*L
� T*D
= T*R
- T*D
= T*(R-D)
= T*h. De
este modo vemos que, despreciando la masa de la biela, el momento sobre el triangulo
delantero proveniente del pedaleo es como si hubi�semos tirado de la cadena
desde un punto del triangulo delantero que est� a una distancia perpendicular
"h" por encima del pivote � un resultado muy interesante ( ver en
la siguiente p�gina Ola Helenius un argumento muy interesante acerca de este
resultado). En todo caso uno debe de ir con cuidado de no llevar este argumento
demasiado lejos ya que anteriormente hemos demostrado que al aumentar el radio
del plato y del pi��n disminuimos la tensi�n de la cadena. tSC
representa el momento en el basculante producto de la
tensi�n de la cadena (es decir, las fuerzas sobre el pedal). Otra vez, considerando
que en la pr�ctica el pivote principal y el eje de pedalier est�n pr�ximos entre
s�, podemos aproximar las fuerzas del basculante en el pivote y las fuerzas
aplicadas en el eje de pedalier provenientes del pedaleo. Con esta aproximaci�n
tenemos que: Para
que exista un equilibrio de momentos entre el triangulo delantero y el basculante
en el pivote principal, desearemos que las dos partes giren al un�sono � es
decir, queremos que aF
= aS.
Despejando las alfas en las ecuaciones 3) y 4) e igualando entre si tenemos
que: Y
si ahora despejamos h tendremos: Esta
es la ecuaci�n de equilibrio de momentos para el pivote principal en relaci�n
con la l�nea de la cadena para un dise�o de suspensi�n monopivote (con el pivote
cerca del eje de pedalier, lo que suele ocurrir en la mayor�a de los casos). Al
principio puede creerse que h depende de T, ya que T aparece en denominador
de los dos t�rminos, no estamos seguros pero creemos que T siempre aparecer�
como un factor en todos los momentos, con la excepci�n de los que provienen
de la horquilla delantera. As� que, salvo en el caso anterior, h no depende
de T. [En el apartado "Algunos c�lculos suplementarios sobre la teor�a
del pivote en la l�nea de la cadena" incluido en los ap�ndices pondremos
un ejemplo de c�mo los momentos pueden eliminar T de la ecuaci�n 8).] Vamos
a sacar algunas conclusiones de la ecuaci�n 8): Primero,
observamos que los momentos de inercia de los dos cuerpos aparecen en todas
las expresiones, esto quiere decir que es imposible desarrollar una teor�a cuantitativa
sobre las suspensiones sin tener en cuenta la distribuci�n de masas. La distribuci�n
de masas tambi�n deber� tenerse en cuenta en el resto de tipos de suspensi�n.
Esto demuestra que no es posible hacer una teor�a de las que nosotros llamamos
Teor�as de "Puntos Especiales". Estas teor�as afirman que cuando la
continuaci�n de la l�nea de la cadena pasa por un punto determinado del triangulo
delantero, la suspensi�n es independiente del pedaleo, independientemente del
resto de consideraciones, entre ellas la distribuci�n de masas del conjunto. La
segunda cosa que observamos es que el valor de los momentos var�a a lo largo
del tiempo, por lo que "h" tambi�n va a depender del tiempo. Podemos
ver ahora que no existe un punto ideal que funcione durante todo el ciclo del
pedaleo. Ademas, la intuici�n nos dice que, cuando el ciclista realiza una pedalada,
el conjunto del sistema, rotar� respecto al eje trasero (a �
0). Entre una pedalada y otra el conjunto volver� a bajar, de una manera que
no mantiene inactivo al amortiguador, a no ser que exista una fricci�n por parte
de los pivotes. Esto nos lleva a la conclusi�n de que es imposible crear un
tipo de suspensi�n trasera totalmente independiente del pedaleo, a no ser que
exista una gran fricci�n est�tica. La
caracter�stica de dependencia del tiempo de los sistemas monopivote tambi�n
sucede en el resto de los dise�os, ya que los cambios en la orientaci�n de los
miembros a lo largo de la pedalada se dan en todos los dise�os. En particular
diremos que, un dise�o monopivote puede ser tan neutral ante la pedalada como
cualquier otro dise�o de paralelogramo deformable. Los
efectos del pedaleo en la suspensi�n suelen ser peque�os pero quer�amos dejar
claro de que las teor�as que dicen haber eliminado este problema de una manera
total no son ciertas. (mas informaci�n en la secci�n "Teor�as de Puntos
Especiales"). Cuando
se consigue un dise�o de suspensi�n con poca interacci�n con la pedalada la
fricci�n de los pivotes puede eliminar pr�cticamente el movimiento de la suspensi�n.
Los efectos producidos por la interacci�n con el pedaleo son peque�os comparados
con los producidos por un obst�culo, por lo tanto un dise�o adecuado con una
cantidad de fricci�n tambi�n adecuada puede eliminar pr�cticamente todas las
oscilaciones y al mismo tiempo ser suficientemente sensible para absorber los
obst�culos. Por
�ltimo, y de un modo intuitivo creemos que, para cualquier tipo de suspensi�n,
mientras menos se extienda el amortiguador trasero durante una pedalada mas
lo har� la horquilla delantera. La proporci�n de activaci�n ideal en cada amortiguador
ser� la que minimice una reacci�n conjunta. 3) Relaci�n
de velocidad de la suspensi�n. Lee
esta secci�n si: Quieres
ver un an�lisis de la puesta a punto de las suspensiones desde el punto de vista
del An�lisis de Trayectorias. S�ltate
esta secci�n si: No
est�s interesado en el tema. No
vamos a dedicar demasiado tiempo a este apartado ya que este tema es uno de
los �ltimos que deben de preocupar a un futuro comprador. Todos los tipos de
suspensi�n pueden dise�arse para que tengan la Relaci�n de Velocidad (nos referimos
al tipo de progresividad que la bieleta o el basculante imprime al amortiguador)
de suspensi�n que mas nos interese y normalmente todos los modelos funcionan
correctamente con su amortiguador de origen. La Relaci�n de Velocidad es algo
que solo interesa a los mas preocupados por las suspensiones y que est�n interesados
en cambiar amortiguadores de aire-aceite por amortiguadores de muelle y aceite
que generalmente tienen una Relaci�n de velocidad interna diferente a los de
aire. Emparejar un cuadro con una relaci�n de velocidad de tipo Falling (que
va disminuyendo) y un amortiguador lineal de muelle aceite no dar� un buen resultado,
como tampoco lo har�a un cuadro con una relaci�n de velocidad de tipo muy Rising
(que va aumentando) con un amortiguador de aire-aceite. En
cualquier caso, el tema de la relaci�n de velocidad va a aparecer en otras partes
de este trabajo, as� que vamos a estudiar las caracter�sticas mas importantes. Todos
los muelles tienen una relaci�n de velocidad y una suspensi�n no es mas que
un tipo de muelle. Definimos
una direcci�n X que representa el recorrido de compresi�n del amortiguador.
La "Relaci�n de Velocidad" es una funci�n de X, Mientras mas pendiente
tenga esta funci�n mas dif�cil ser� comprimir el amortiguador. Para un amortiguador
de muelle en equilibrio la funci�n es pr�cticamente lineal. Si la funci�n es
c�ncava vista desde arriba (el amortiguador ser� cada vez mas dif�cil de comprimir),
diremos que la relaci�n de velocidad es de tipo "Rising". Y si es
c�ncava desde abajo (el amortiguador es cada vez mas f�cil de comprimir), diremos
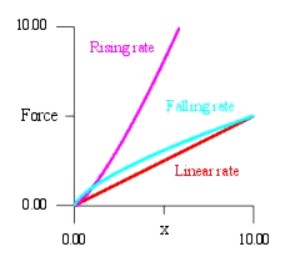
que es de tipo "Falling". La
figura 2.13 contiene un gr�fico ene le que se muestran los distintos tipos. Figura
2.1 El
tipo de relaci�n de velocidad de un dise�o es la suma de las caracteristicas
del amortiguador y las inherentes al dise�o del basculante y bieletas en el
caso de que existan. La
relaci�n de velocidad interna de un amortiguador var�a entre la de tipo Lineal
y la de tipo "Rising". Los amortiguadores de muelle suelen ser lineales,
mientras que los de aire son mas de tipo "Rising". Todos los cuadros
permiten un rango de posibilidades a la hora de elegir amortiguadores, cuyas
medidas se est�n estandarizando en dos longitudes diferentes. A partir de ahora
nos centraremos mas en la geometr�a de los dise�os ya que el tipo de amortiguador
no interviene en este punto. La
contribuci�n del dise�o del triangulo trasero a la Relaci�n de Velocidad la
determina la forma en que anclamos el amortiguador, la posici�n del eje trasero
y delantero y el movimiento del triangulo delantero en relaci�n con el resto
del conjunto. La posici�n del eje delantero estabiliza la orientaci�n del cuadro
con el suelo pero generalmente no la vamos a tener en cuenta. La altura del
eje de pedalier suele ser en la mayor�a de los casos de 33 � 1.25 cm por lo que (suponiendo
una medida de longitud de la horquilla habitual) la orientaci�n del cuadro vendr�
determinada por el eje trasero y el de pedalier. Repetimos
otra vez que no vamos a dedicar demasiado tiempo a este aspecto pero vamos a
poner un ejemplo de la contribuci�n que tiene la colocaci�n y el movimiento
del amortiguador en el cuadro en el comportamiento de la suspensi�n. Establecemos
el sitema de referencia en el triangulo delantero. El anclaje del amortiguador
trasero describe una trayectoria circular alrededor de un pivote, el pivote
principal en el caso de un dise�o monopivote y la articulaci�n superior (la
de la bieleta) en el caso de un sistema de 4 articulaciones. (Lo que sigue se
puede aplicar en ambos casos). Si
la tangente del movimiento del anclaje del amortiguador apunta hacia el anclaje
delantero del amortiguador podemos decir que la geometr�a de la bieleta o del
basculante no influye en las caracteristicas del amortiguador, ser�a un dise�o
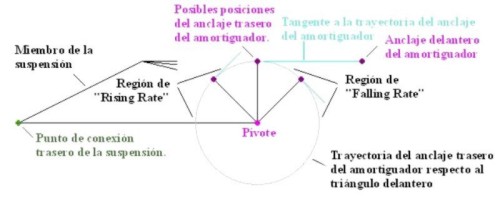
neutral. Si el amortiguador es lineal la suspensi�n ser� tambi�n lineal. La
figura 2.14 muestra un gr�fico con las distintas posibilidades de anclaje del
amortiguador. Cuando la suspensi�n se comprime, si la tangente del anclaje trasero
se mueve acercandose a la direcci�n del amortiguador, podemos decir que se aumenta
la Relaci�n de Velocidad. Si la tangente se aleja de la direcci�n del amortiguador
lo que ocurre es que reducimos la relaci�n de velocidad. Esto se debe a que
en una rotaci�n la mayor velocidad de compresi�n se obtiene cuando los dos pivotes
est�n alineados con la tangente del recorrido del anclaje trasero. Figura
2.14 En
el caso de un dise�o monopivote, el miembro de la suspensi�n es el triangulo
trasero, y la conexi�n trasera es el eje de la rueda . En el caso de un dise�o
de 4 Barras, el miembro de la suspensi�n es la bieleta superior y la conexi�n
trasera es la articulaci�n trasera. En
ambos casos, cuanto mas grande sea el radio de giro del anclaje trasero del
amortiguador, la curvatura de la funci�n "Relaci�n de Velocidad" ser�
mayor. Por el otro lado, cuanto mas grande sea el tama�o del miembro de la suspensi�n
mayor importancia tendr� la Relaci�n de Velocidad interna del amortiguador.
Esto
es pr�cticamente toda la teor�a de los dise�os Monopivote (sin contar el recorrido
de la suspensi�n). Para un dise�o del tipo 4 barras, debemos de hacer un an�lisis
similar entre la tangente del recorrido de la articulaci�n trasera y el eje
trasero. En cualquier posici�n del recorrido, si la tangente apunta al eje de
la rueda, el amortiguador se comprimir� menos en relacion con el desplazamiento
del eje de la rueda. En la mayor�a de los dise�os del tipo 4 Barras este pivote
tien un recorrido que hace didminuir la Relaci�n de velocidad, y por lo tanto,
mientras mayor sea el radio de este pivote, mayor ser� la curvatura de la funci�n.
Los recorridos del anclaje trasero del amortiguador y de la articulaci�n superior
de la bieleta son los que determinan el comportamiento general de un dise�o
de 4 Barras, sin contar el recorrido de la suspensi�n. |