![]()
Visits since 9 June 1998
Atmospheric flows exhibit irregular (chaotic) space-time fluctuations on all scales ranging from climate(kilometers-years) to turbulence(millimeters-second) and is a representative example of turbulent fluid flows. Dynamical systems in nature ,i.e., systems that change with time, such as fluid flows, heartbeat patterns, spread of infectious diseases, etc., exhibit nonlinear (unpredictable) fluctuations. Conventional mathematical and statistical theories deal only with linear systems and the exact quantification and description of nonlinear fluctuations was not possible till the identification in the 1970s by Mandelbrot (1977;1983 References ) of the universal symmetry of selfsimilarity, i.e. fractal geometry underlying the seemingly irregular fluctuations in space and time (Schroeder, 1991; Stanley, 1995References). The study of selfsimilar space-time fluctuations generic to dynamical systems, now (since 1980s) ,belongs to the newly emerging multidisciplinary science of nonlinear dynamics and chaos (Gleick,1987References)
Selfsimilar fluctuations in space and time imply long-range spatiotemporal correlations and are recently identified as signatures of self-organized criticality (Bak et. al., 1988References). Self-organized criticality in atmospheric flows is manifested as the fractal geometry to the global cloud cover pattern concomitant with inverse power law form for power spectra of temporal fluctuations documented and discussed in detail by Lovejoy and his group (Lovejoy,S.,1982;Lovejoy and Schertzer, 1986a,b; Schertzer and Lovejoy;1991,1994;Tessier et. al., 1993,1996 and all the references thereinReferences). Standard meteorological theory cannot explain satisfactorily the observed self-organized criticality in atmospheric flows (Tessier et. al., 1993,1996). Also, traditional mathematical models for simulation and description of irregular fluctuations in general, and atmospheric flows in particular are nonlinear and finite precision computer solutions are unrealistic(chaotic) because of deterministic chaos(Gleick,1987). In this paper, an alternative nondeterministic cell dynamical system model for atmospheric flows developed by Mary Selvam(1990References) is summarized. The model predicts the observed self-organized criticality as intrinsic to quantumlike mechanics governing flow dynamics. The model concepts enable universal quantification for the observed nonlinear variability in terms of the statistical normal distribution. The model predictions are in agreement with several standard long-term climatological data sets for meteorological parameters.The implications of model concepts for long-term climate change prediction are discussed.
The paper is organized as follows: Section 2(2. Nonlinear Dynamics and Chaos) gives a detailed summary of general concepts in the newly emerging science of nonlinear dynamics and chaos and applications for quantifying the observed atmospheric flow patterns. Limitations of current concepts in standard meteorological theory and deterministic chaos in model solutions are discussed in Section 3. An alternative nondeterministic cell dynamical system model for atmospheric flows is summarized in Section 4. Details of climatological data sets used and analyses techniques are presented in Section 5. Section 6 contains results and discussions. Possible applications of model concepts for prediction of climate variability and climate change are given in Section 7. Conclusions regarding validity of model concepts and predictions are given in Section 8.
2. Nonlinear Dynamics and Chaos: A Multidisciplinary Science
The new science of nonlinear dynamics and chaos (Gleick, 1987 References) deals with unified concepts for fundamental aspects intrinsic to the complex (nonlinear) and apparently random (chaotic) space-time structures found in nature. Scientific community at large will derive immense benefit in terms of new insights and powerful analytical techniques in this multidisciplinary approach to quantify basic similarities in form and function in disparate contexts ranging from the microscopic to the macroscopic scale.
The apparently random, noisy or irregular space-time signals (patterns) of a dynamical system, however, exhibit qualitative similarity in pattern geometry on all scales and are therefore correlated. In general, the spatiotemporal evolution of dynamical systems trace a zigzag (jagged) pattern of alternating increase and decrease, associated with bifurcation or branching on all scales of space and time, generating wrinkled or folded surfaces in three dimensions. Representative examples for time series of some meteorological parameters used in the present study are shown in Figure 1.
FIGURE 1
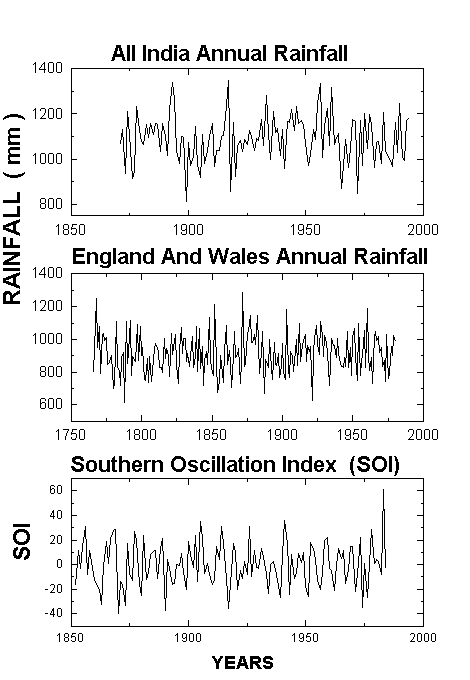
Physical, chemical, biological and other dynamical systems exhibit similar universal irregular space-time fluctuations. A fascinating aspect of patterns in nature is that many of them have a universal character(Dennin et.al., 1996References).
Irregular space-time fluctuations associated with basic bifurcation or branching geometry of wrinkles or folds on all scales is associated with the symmetry of selfsimilarity under scales transformation or just selfsimilarity(Liu, 1992References). A symmetry principle is simply a statement that something looks the same from certain different points of view. Such symmetries are often called principles of invariance (Weinberg, 1993References). The fundamental similarity or universality in the basic geometric structure, namely irregularity, was identified as fractal in the late 1970s by Mandelbrot (1977,1983References). Fractal geometry is ubiquitous in nature, the fine structure on all scales being the optimum design for sustenance and growth of large scale complex systems comprised of an integrated network of sub-units. The branching architecture of river tributaries, bronchial tree, tree branches, lightning discharge, etc., serve to collect/disperse fluids over a maximum surface area within a minimum volume. Fine scale fluctuations help efficient mixing of fluids such as pollution dispersion in the atmosphere. The basic similarity in the branching form underlying the individual leaf and the tree as a whole was identified more than three centuries ago in botany (Arber,1950References). The importance of scaling concepts were recognized nearly a century ago in biology and botany where the dependence of a property y on size x is usually expressed by the allometric equation y=AxB where A and B are constants (Thompson,1963; Strathmann, 1990; Jean, 1994; Stanley,Amaral,Buldyrev, Goldberger et. al., 1996References). This type of scaling implies a hierarchy of substructures and was used by D'Arcy Thompson for scaling anatomical structures, for example, how proportions tend to vary as an animal grows in size(West, 1990a). D'Arcy Thompson (1963, first published in 1917) in his book On Growth and Form has dealt extensively with similitude principle for biological modelling.Rapid advances have been made in recent years in the fields of biology and medicine in the application of scaling (fractal) concepts for description and quantification of physiological systems and their functions(Goldberger,Rigney and West, 1990;West, 1990a,b; Deering and West,1992;Skinner,1994;Stanley,Amaral,Buldyrev,Goldberger et. al., 1996References). In meteorological theory, the concept of selfsimilar fluctuations was introduced in the description of turbulent flows by Richardson(1965, originally published in 1922) ,Kolmogorov(1941,1962) ,Mandelbrot(1975) (Kadanoff 1996) and others(see Monin and Yaglom ,1975 for a reviewReferences).