![]()
Visits since 6 July 1998
3. Nonlinear Dynamics and Chaos in Iterative Processes
Standard models for turbulent fluid flows in meteorological theory cannot explain satisfactorily the observed multifractal (space-time) structures in atmospheric flows(Tessier et al.,1993,1996 References). Traditionally, meteorological theory is based on the following concepts. The turbulent atmospheric flows are governed by the mutual interaction of a large number of factors, i.e. variables such as pressure, temperature, moisture content, wind speed, etc. The prediction of future flow pattern is based on mathematical equations for the rate of change 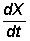 of component variable X with time t. The rate of change with time
of component variable X with time t. The rate of change with time 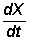 of any variable is generally a nonlinear function of all the other interacting variables and therefore analytical solution for X is not available. The evaluation of any variable X with time is then computed numerically from the iterative equation
of any variable is generally a nonlinear function of all the other interacting variables and therefore analytical solution for X is not available. The evaluation of any variable X with time is then computed numerically from the iterative equation
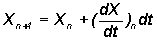 (2)
(2)
where the subscript n denotes the time step and the rate of change 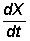 is assumed to be continuous for small changes in time dt, an assumption based on Newtonian continuum dynamics. The successive values of X are then computed iteratively, a process known as numerical integration. The prediction equation for the variable X has intrinsic error feedback loop since the value of X at each step is a function of its earlier value in such numerical integration computational techniques. The fundamental (basic) error in numerical computations is the round-off error of finite precision computations.Blank(1994 References) mentions that when solving differential or other dynamical systems on a computer, the effects of finiteness(round-off) can sometimes be very drastic.When we work with fixed precision system, not all real numbers are even representable and arithmetic does not have the properties that we are used to(Corless et.al.,1990).Lorenz(1989 References) has discussed chaotic behaviour when continuum equations are solved numerically as difference equations.Climate modelling concepts has come under criticism lately since uncertainty in input parameter values can give drastically different results(Kerr,1994).Mary Selvam (1993a References) has shown that round-off error approximately doubles on an average at each step of iteration. Such error doubling at each step in numerical integration will result in the round-off error propagating into the mainstream (digits place and above) computation within 50 iterations using single precision (7th decimal place accuracy) digital computers. In addition, any uncertainties in specifying the initial value of the variable X will also grow exponentially with time and give unrealistic solutions. Numerical solutions are therefore sensitively dependent on initial conditions. Deterministic governing equations, namely evolution equations such as Equation 2. which are precisely defined and mathematically formulated give chaotic solutions because of sensitive dependence on initial conditions. Finite precision computer realizations of nonlinear mathematical models of dynamical systems therefore exhibit deterministic chaos. Computed model solutions are therefore mere mathematical artifacts of the universal process of round-off error growth in iterative computations(Mary Selvam,1997). Mary Selvam (1993a References) has shown that the computed domain is the successive cumulative integration of round-off error domains analogous to the formation of large eddy domains as envelopes enclosing turbulent eddy fluctuation domains such as in atmospheric flows. Computed solutions, therefore qualitatively resemble real world dynamical systems such as atmospheric flows with manifestation of self-organized criticality. Self-organized criticality, i.e. long-range spatiotemporal correlations, originates with the primary perturbation domains corresponding respectively to round-off error and dominant turbulent eddy fluctuations in model and real world dynamical systems. Computed solutions, therefore, are not true solutions. The vast body of literature investigating chaotic trajectories in recent years (since 1980) document, only the round-off error structure in finite precision computations. Stewart(1992b References) mentions that in the absence of analytical (true) solutions the fidelity of computed solutions is questionable. Historically,deterministic chaos in computed solutions was identified nearly a century ago by Poincare in his study of the three body problem (Poincare, 1892 References). Lack of high speed computational machines precluded exhaustive studies of nonlinear behavior and approximate linearized solutions of nonlinear systems alone were studied. With the advent of electronic digital computers in late 1950s, Lorenz (1963 References) identified deterministic chaos in a simple model of atmospheric flows. Lorenz's result captured the attention of scientists in all branches of science since a simple set of equations exhibits chaotic behaviour similar to the complex, irregular (unpredictable) fluctuations exhibited by real world dynamical systems. Till then it was believed that complex behavior results from complexity in the governing parameters and the mathematical formulations. Lorenz's model demonstrated that simple models can demonstrate complex behavior of real world dynamical systems.
is assumed to be continuous for small changes in time dt, an assumption based on Newtonian continuum dynamics. The successive values of X are then computed iteratively, a process known as numerical integration. The prediction equation for the variable X has intrinsic error feedback loop since the value of X at each step is a function of its earlier value in such numerical integration computational techniques. The fundamental (basic) error in numerical computations is the round-off error of finite precision computations.Blank(1994 References) mentions that when solving differential or other dynamical systems on a computer, the effects of finiteness(round-off) can sometimes be very drastic.When we work with fixed precision system, not all real numbers are even representable and arithmetic does not have the properties that we are used to(Corless et.al.,1990).Lorenz(1989 References) has discussed chaotic behaviour when continuum equations are solved numerically as difference equations.Climate modelling concepts has come under criticism lately since uncertainty in input parameter values can give drastically different results(Kerr,1994).Mary Selvam (1993a References) has shown that round-off error approximately doubles on an average at each step of iteration. Such error doubling at each step in numerical integration will result in the round-off error propagating into the mainstream (digits place and above) computation within 50 iterations using single precision (7th decimal place accuracy) digital computers. In addition, any uncertainties in specifying the initial value of the variable X will also grow exponentially with time and give unrealistic solutions. Numerical solutions are therefore sensitively dependent on initial conditions. Deterministic governing equations, namely evolution equations such as Equation 2. which are precisely defined and mathematically formulated give chaotic solutions because of sensitive dependence on initial conditions. Finite precision computer realizations of nonlinear mathematical models of dynamical systems therefore exhibit deterministic chaos. Computed model solutions are therefore mere mathematical artifacts of the universal process of round-off error growth in iterative computations(Mary Selvam,1997). Mary Selvam (1993a References) has shown that the computed domain is the successive cumulative integration of round-off error domains analogous to the formation of large eddy domains as envelopes enclosing turbulent eddy fluctuation domains such as in atmospheric flows. Computed solutions, therefore qualitatively resemble real world dynamical systems such as atmospheric flows with manifestation of self-organized criticality. Self-organized criticality, i.e. long-range spatiotemporal correlations, originates with the primary perturbation domains corresponding respectively to round-off error and dominant turbulent eddy fluctuations in model and real world dynamical systems. Computed solutions, therefore, are not true solutions. The vast body of literature investigating chaotic trajectories in recent years (since 1980) document, only the round-off error structure in finite precision computations. Stewart(1992b References) mentions that in the absence of analytical (true) solutions the fidelity of computed solutions is questionable. Historically,deterministic chaos in computed solutions was identified nearly a century ago by Poincare in his study of the three body problem (Poincare, 1892 References). Lack of high speed computational machines precluded exhaustive studies of nonlinear behavior and approximate linearized solutions of nonlinear systems alone were studied. With the advent of electronic digital computers in late 1950s, Lorenz (1963 References) identified deterministic chaos in a simple model of atmospheric flows. Lorenz's result captured the attention of scientists in all branches of science since a simple set of equations exhibits chaotic behaviour similar to the complex, irregular (unpredictable) fluctuations exhibited by real world dynamical systems. Till then it was believed that complex behavior results from complexity in the governing parameters and the mathematical formulations. Lorenz's model demonstrated that simple models can demonstrate complex behavior of real world dynamical systems.
The computed trajectory is plotted graphically in phase space of dimension m where m is the number of variables representing the dynamical system. For example, a particle in motion can be represented completely at any instant by its position and momenta in the x, y and z directions, i.e. 6-dimensional phase space. The line joining the successive points in time gives the trajectory of the particle in phase space. The trajectory traces the strange attractor , so named because of its strange convoluted shape being the final destination of all trajectories in the phase space. Two trajectories, initially close together diverge exponentially with time though still within the strange attractor domain, thereby exhibiting sensitive dependence on initial conditions or deterministic chaos. The strange attractor exhibits selfsimilar fractal geometry similar to the space-time fractal structure or self-organized criticality exhibited by real world dynamical systems. Mary Selvam (1993a References) has shown that the strange attractor has the quasicrystalline structure of the quasiperiodic Penrose tiling pattern. There is a very close similarly between the geometrical patterns generated during iterative computations and those found in nature (Jurgen et al., 1990; Stewart, 1992a References). Iterative computations generate patterns strongly reminiscent of plant forms and clearly these curious configurations show that the rules responsible for the construction of elaborate living tissue structures could be absurdly simple (Dewdney, 1986 References).
In summary, selfsimilar space-time structures or self-organized criticality is ubiquitous to dynamical systems in nature and also to mathematical models of dynamical systems which incorporate finite precision iterative computations with resultant feedback and magnification of round-off error primarily, in addition to initial errors. Iterative computations result in the cumulative addition (integration) of the progressively increasing round-off error. Persistent perturbations, though small in magnitude are therefore capable of generating complex space-time structures with fractal selfsimilar geometry because of feedback with amplification.
Back to Climate Dynamics,Chaos and Quantum Mechanics