FUNDAMENTALS OF PROCESSING
In this section we will discuss the properties of fluids, the effect of pressure, heat and characteristics of fluid flow. A fluid is any substance which easily yields to pressure, which
has no definite shape and which will flow readily. Both liquids and gases conform to this requirement and are classified as fluids. Although we have already learned many differences the characteristics of these two states of matter, they also have certain properties in common. For
instance, both have inertia, impenetrability and density. Both these can be pumped mechanically from one place to another, stored in containers of any shape and both take shapes of their containers. The greatest difference between gases and liquids is the fact that gases can be com-
pressed and liquid, for practical purposes, cannot be compressed.
In studying the properties of fluids we must understand the differences between the terms force, weight and pressure. In simple terms force means a push or a pull, weight indicates heaviness and
pressure means the force per unit area of the surface acted upon. Hence pressure can be related to weight and force as follows.
Force
Press = Area acted upon
Press = weight
Area acted upon
Pressures on fluids at rest
Pressure has been earlier defined as the force per unit area. There are two kinds of pressures that can exist on a fluid at rest. They are (a) pressure due to gravity or static pressure, (b) Induced
pressure. The static pressure is due to the weight of the fluid and the induced pressure is the pressure applied by an external force. One of the interesting fact about the behaviour of fluids is that pressure has no definite direction regardless of where it is measured. At any point in a fluid under pressure, the downward pressure equals the other.
Static Pressure
Everything on the surface of earth exists under the static pressure created by air, which we call as atmospheric pressure. As mentioned previously, this pressure is I. 033 kg/cm 2 at sea level. If we were to get down to a level -40 meters higher than the surface of earth the pressure will reduce to the extent of the reduced column of air above and will be equal to
0-00129 X 40 X 100
I .033 — 1000 = I .033 — 0.00516=1 -02784 kg/cm2 A.
since the density of air is 0.00129 gm/cc at atmospheric pressure.
Similarly if a body is immersed in a tank of water to a depth of 50 meters the pressure the body will be subjected to is the sum of the atmospheric pressure and the static pressure due to the column of liquid. The static pressure of the liquid will be exerted on the body in all directions.
Induced Pressure
Before pressure can be induced in a fluid, it must be put into a vessel which can be sealed off from the atmosphere. Induced pressure is in addition to static pressure and the sum of both is the total
pressure when the fluid is at rest. Pressure can be induced by heating or mechanical force. If we take a container sealed off from atmospheric pressure and containing its own vapour and liquid and if this container is heated, the pressure increases. This induced pressure is the same in both the substances.
When force is applied to a given area on the surface of an enclosed fluid^ that force will be transmitted without gain or loss of intensity to every equal area in the vessel. This is known as Pascals Law. Any applied force induces pressure In an enclosed fluid. This pressure exerts against the walls of the vessel. Regardless of the shape of the vessel, this pressure acts at right angles to the vessel walls. An important application of the Pascals law is the hydraulic lift. A small force applied to a small area induces pressure. Even when the induced pressure is small, if it can be applied to another large area, it will exert a larger force. Work is the product of a force and distance through which the force succeeds in moving the object acted upon. Therefore the induced pressure in a small area gives large force in a larger area, but will move the object for a shorter distance.
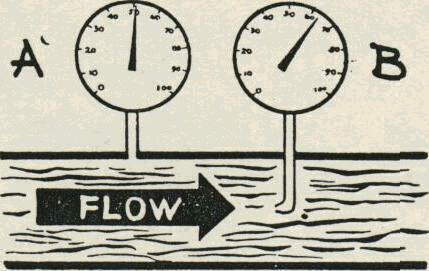
Pressure measurements in pipelines vary according to how the pressure gauge is installed. The figure below show two ways in which the pressure gauges are installed. The gauge A will read the static and induced pressures whereas gauge B will measure the static pressure, induced pressure and velocity pressure. The velocity pressure is the pressure that is created by the inertia of moving a mass of liquid.

Flow
Fluids tend to move in thin sheets, called laminae. As long as they are moving in parallel lines at the same speed there is no tendency for one layer to drag on another. This ideal condition is called streamline flow or laminar flow. However this condition never exists in actual practice. Molecules of all liquids have a tendency to cling together i. e., have the property of cohesion. This causes an internal friction which has been previously defined as viscosity. Also, the fluids tends adhere to the other substances like pipewalls. This adhesion is the primary problem in fluid flow, because adhesion causes drag on laminae at the pipewalls and the cohesive forces create dragon the adjacent laminae near the pipewalls finally resulting in turbulant flow. This drag caused by adhesion at the pipewalls causes the laminae to break and causes a great deal of congestion in the fluid which flows. The laminae in a pipe can be visualised as cylinders of fluid one inside the other. The outside cylinders cling against the pipewall causing the
next cylinder to break its flow pattern which in turn acts on the next cylinder and so on towards the centre of the pipe. Each of these cylinders is disturbed slightly lesss than the one before it. Consequently, if the pipe is large enough, the interior fluid is able to flow smoothly. The velocity is the greatest at the pipe axis and decreases sharply to nearly zero at the pipewall.
The overall effect of the turbulant flow is a reduction in effective pipe size.
Relation between cross-sectional sectional area, quantity of flow and velocity
Total quantity of liquid that enters a pipe must leave the pipe from the other end immaterial of cross-section, as liquids are incompressible. If the liquid is being pumped through a pipe having different cross-sectional area, the same quantity of liquid must pass every point in the same length of time. Consequently, the velocity of flow must change every time the diameter changes. The volume of liquid passing any cross-sectional area of the pipe is the product of velocity and
cross-sectional area at the point. This is expressed by the formula
Q = A x V
where Q is the Quantity of liquid, A is the cross-sectional area of the pipe and V is the velocity of the liquid.
Let us consider a case of pipeline where the diameter of the pipe is reduced to half its original size. The cross-sectional area of the reduced section is calculated as follows:
The original cross-sectional area A1 = II D12 (D1 is the original diameter)
4
and reduced cross-sectional area A2 = II D22 (D2 is the reduced diameter)
4
Since D2 = D1 , A2 = II * (D1)2
2 4 (2)2
= II * (D1)2
4 4
= A1
4
For a fixed quantity of flow, the velocities Vi in the original
section and the velocity Vz in the reduced section are related
follows:—
Q = A1 * V1 = A2 * V2
Therefore, V2 = A1 * V1 = A1 * V1* 4/A1
A2
= 4 A1
To generalise the example, the velocity of the flow of a liquid through a pipe changes inversely proportional to the square of its diameter for a given flow.
Resistance to flow
Fluid will flow in a pipeline if there is a difference in the pressure between its ends. The pressure difference can be static pressure resulting from a difference in elevation of the ends or it may be an induced pressure difference created by a pump. In oil refinery, most pressures are induced with pumps. In both the cases, some pressure loss occurs in any pipeline through which fluid flows.
The magnitude of the pressure loss in a piping system depends on a number of factors, some of which are:
1. Line size (pipe diameter)
2. Line length.
3. Roughness of inside the pipe surface.
4. Pipe bends.
5. Velocity of fluid flow.
6. Viscosity of the fluid.
7. Density of the fluid.
Line size affects the resistance to fluid flow through turbulance. When pipe diameter is small, streamline flow is not possible. The line length causes more resistance to flow because it multiplies all the other resistance factors. Surface roughness produces turbulance and its effect is more objectionable in small diameter pipeline. Turbulance can occur in a perfectly smooth pipe if the velocity is high because adhesion disrupts the flow pattern of laminae near the pipewall. Pipe bends create resistance to flow in two ways. Firstly because pipe bend is usually a point of roughness and secondly because force is required to change the direction of flow. At any pipe bend, the force required to change the direction of flow mostly acts against the direction of flow.
Excessive fluid velocity in a system can greatly increase the pressure drop. As the speed of the flow increases, turbulance begins and the loss of pressure down-stream increases. As previously mentioned, the liquid in a pipe tends to flow in thin cylinders or laminae. At low velocities, these cylinders shear past one another easily at different speeds. This type of flow allows the greatest quantity of liquid to be moved with the least possible effort. But to achieve this condition larger diameter pipes are required which becomes uneconomical. Normally, piping systems are designed for a fluid velocity near to the velocity where turbulance starts. This velocity is called critical velocity.
Critical velocity is related to the viscosity and density of the fluid. The change from the streamlined flow to a turbulant flow occurs when the flow rate, pipe diameter and viscosity reach a certain ratio values. The practical application of streamline or turbulant flow is more important for designing than for operation. Pipes are designed for near stream-line flow where the pressure drops through the line must be kept low and design for turbulant flow is made where mixing and heat transfer are desired. A typical chart below shows how the pressure drop increases with the velocity of fluid flow.
pressure drop
Rate of Flow
Change in the density will also affect the pressure drop. An increase in density will decrease pressure drop. Density of a liquid increases with cooling and therefore the pressure drop reduces if the product is cooler. If two fluids having same viscosity, but different densities are pumped through similar piping system at the same velocity, more dense fluid creates less turbulance and therefore less pressure drop. The reason for this is the deflection of the laminae is less in case of denser liquid than lighter liquids.
The above-mentioned propertiss of liquids are used in the refinery to measure flow rates. The pressure drop through a cross-section of a pipe increases proportional to the square of the velocity. The pressure drop is also affected by viscosity and density as mentioned earlier.
The venturi tube is a device that is used to measure fluid flow using the pressure differential created by increased velocity. Since the total head in the system is the same at all points, excluding friction in a given system, the drop in pressure through the venturi increases as the velocity is greater. The friction pressure drop is minimised by shaping the venturi to get higher velocity in a stream-lined manner. The difference in pressure between low velocity point A and high velocity point B (called throat) is measured and related to the amount of fluid
flowing through,the venturi tube. (Refer fig. below)
The most common means of measuring fluid flow in the refinery is by using an orifice plate. It uses the same principle like a venturi tube and is cheaper although not so stream-lined.
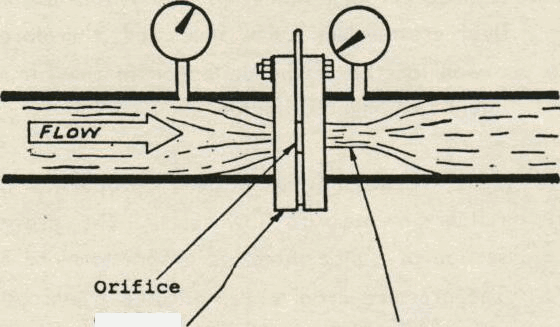
Orifice plate Vena Contracta
Basic Principles of Energy
A body is said to possess energy when on account of Its condition it is capable of doing work. By virtue of its position, velocity, temperature, electric pressure or chemical composition a body may be capable of doing work. Heat, electricity, magnetism etc., are different forms of energy. Energy is measured in different units in the English and Metric system and can be converted into other system easily. The energy possessed by a body by virtue of its position is called potential energy. A common example is water stored in reservoirs at high level. The energy possessed by a body by virtue of its velocity is called kinetic energy. Energy can be converted from one form to other.
Work is the useful product of expended energy. It is the result of force being applied through a distance and is measured in gram-centimeter. By this definition a man does not work holding a heavy load as the distance moved is zero. But the person is spending heat energy to hold the heavy load and therefore the conclusion is that it is possible to spend energy without doing useful work.
Power is the time rate of doing work. The familiar term horse power is defined as the work done to move 550 Ibs. weight by one foot in one second.
Heat
Heat is a form of energy. Heat flows from one mass to another because of the temperature difference between them and it is independant of the weight of the mass. Heat energy represents a store of useful work and is a quantity. If a work requirement is small, only part of the total quantity will have to be used.
Measurement of heat :
Heat is the quantity of energy flowing from one mass to another. It is customary to think of heat in terms of temperature, but temperature is indication of the level of heat or intensity of the heat
and does not directly indicate the quantity of heat. Measurement of temperature has been previously discussed.
Heat is measured in gram-calories, kilocalories and British Thermal units (B. T. U.). Since heat is a form of energy it can be expressed in gram-centimeter also. The heat required to raise the temperature of I gm. of water by 1°C (0°C- 1°C) is called calory and the heat required to raise the temperature of one pound of water through
51
one degree Fahrenheit (60°F to 61°F) is called B. T. U. One BTU is
equal to 252 calories. Using the definition the amount of heat required
to raise the temperature of one litre of water at 30°C to its boiling
point of IOO°C can be calculated as follows.
Since specific gravity of water is I, one litre of water weighs 1000 grams. Therefore,
Calories required = Temperature difference X weight
= (100 - 30) X 1000
= 70 X 1000 = 70.000 calories.
Specific Heat
Specific heat is the heat required to raise the temperature one gram of substance through one degree centigrade. By the definition the specific heat of water is 1. It is interesting to note that the specific heat values of all substances are independant of the system of measure used. The specific heat of water is one BTU per pound or I calory per gram. The /specific heat of most of the substances are less than that of water. Specific heat of some of the typical substances are listed below.
Gasoline .... 0.500 Aluminium .... 0.224
Toluene .... 0.400 Copper .... 0.092
Kerosene .... 0.500 Iron .... 0.122
Crude Oil .... 0.500, Sulphur .... 0.175
Coke .... 0.203 Mercury .... 0.033
In general, the more dense a substance, the lower is its specific heat. It is also interesting to note that the common Refinery oils have the same specific heat.
The following formula can be used to calculate heat requirements.
q = w* T * C Where
Q = Quantity of heat required
W= Weight of the substance
T = Temperature differential
C = Specific heat.
Using this formula let us calculate how many calories are required to raise 2000 litres of kerosene from 15°C to 85°C — the specific gravity of kerosene is 0.80.
Q=W X T x C
Weight of 2000 litres =2000 X 0.80 == 1600 grams = W
T= 85 — 15 = 70°C C = 0.500
Therefore, Q = 1600 X 70 X 0.500 = 56,000 calories.
The foregoing heat requirement calculation involves changing the temperature of the substance without change of state (from liquid to gas, etc.) taking place. This is called sensible heat. This term Is used to distinguish it from the additional heat required to change the state of the substance.
Latent Heat
If we take a beaker of water and heat it up, we find the temperature rising. The temperature continues to rise till boiling starts and remains steady at 100°C even though further heat is applied. In this case the heat applied is utilised by the liquid to change its state to vapours. The heat required to change the state of a substance Is called latent heat. The heat required for a solid to change its state to liquid is called latent heat of fusion and that for liquid to change to vapours is called latent heat of vapourisation.
The latent heat of vapourisation of water is 539.6 calories/gram at standard atmospheric pressure. Under less pressure, the latent heat increases and under higher pressure, less latent heat is required. The latent heat of vapourisation of oils is considerably less than that of water. The latent heat of vapourisation of gasoline, kerosene and sulphur are 75, 60 and 66 calories per gram respectively.
The Law of Conservation of Energy
The study of the various forms of energy and the transformation of one kind of energy into another has led to the statement of a very important basic principle of energy known as the conservation of energy. This may be stated as follows. In any body or a system of bodies which is not receiving or giving up energy, the total amount of energy remains unchanged. In other words, energy can never be created or destroyed, but can be transformed from one form to another, the total amount remaining unchanged.
A bullet leaving the muzzle of a gun receives its energy on account of the work done by expanding gases. As it passes through the air, it looses some of its kinetic energy because of friction of air
in the atmosphere. This kinetic energy is transferred to air in the form of heat. When it strikes an object heat will be developed, part of which will be absorbed by the target and part by the bullet fragments. Some part of the energy may get converted to sound and light also. Thus the total energy of the bullet is converted into various forms of energy and will be equal to the initial energy the bullet possessed.
Another example of transformation of energy, which is commonly found in the refinery, is in the boilers. Fuel oil burned in the boiler converts the stored chemical energy into heat energy by combustion. The heat energy is transferred to the water to produce steam with energy stored in the form of heat and pressure. This steam can be used to drive a turbine which transforms the heat and pressure to the kinetic energy. The turbine can be used to drive a generator where the kinetic energy is transformed into electrical energy.
The main purpose of most of the equipments in the refinery is either to change energy from one form to another or to transfer energy from one place to another. A heat exchanger, an electric cable or a compressed air line move or transfer energy from one place to another.
Efficiency
Efficiency is the ratio of output to input. No machine gives out as much energy or power as is put into it in the form it is intended for. There are some losses even in the most perfectly constructed machines. Efficiency is usually expressed as a percentage. For example, if we say that the efficiency of a motor is 80%, it means that only 80% of the energy or electric power received by the motor Is delivered as available driving force and balance used to overcome friction, inertia,
transformed into heat energy, etc. Furnace efficiency, for example, is the percentage of the heat input from the burning fuel to the heat absorbed by the feed stock. If furnace efficiency is 70%, for every 100 calories fired, only 70 calories are absorbed in the process stream and the rest of the energy is used for heating things that the furnace is not intended for.
Energy when it is under control is very useful but can be hazardous when it is out of control. A pound of gasoline can do more damage than a pound of dynamite, since gasoline has more stored chemical energy than dynamite. Compressed air can expel a rock or a piece of metal at a high velocity like a bullet. Equipments moving at high speed contain large amount of kinetic energy. Turbines are known to fly apart when overspeeded and break the casing sending out bits like sharpnels from a bomb.
Heat Transfer
As previously mentioned heat always flows from a higher temperature to a lower temperature. It can flow through all forms of matter as well as exist within it. Heat can be emitted from one body to another. It can also be reflected. Temperature is the indication of heat or energy level.
In general there are three methods of heat transfer. These are known as conduction convection and radiation.
Conduction
Heat that flows from one part of a substance to another part of a substance or from one substance to another by physica contact is said to flow by conduction. The heat felt on the handle of a spoon after keeping it immersed in hot liquid is the result of heat being conducted from the liquid to the handle of the spoon. There are some substances such as stone, wood, plastics, cork which are poor conductors of heat and are called insulators. All metals are good conductors of heat, although there is difference in their conductivity. Liquids and gases are much poorer conductors than metals. Insulating materials like magnesia, glass wool, cork are used in the refinery around pipelines and vessels to prevent loss of heat to the air.
Convection
Heat also can be transferred from one place to another by a moving stream of air or some other fluid. All systems of ventilation or heating of rooms depend on the convection currents which in turn depends on the expansion of the fluids. Any time a gas or a liquid is heated, there is an increase in volume and consequently a decrease in density. The decrease in density causes the fluid to rise upwards and it is replaced by denser fluid surrounding it. Soon the dense fluid will get heated and the process of displacement continues. Thus there is a motion set up and this motion is called convection currents. The convection currents transport the heat from the source to a different area or to a different substance. The convection currents can be caused naturally by a temperature difference creating density difference or they can be caused artificially or boosted by blowers.
Radiation
A third way by which heat can be transferred from one body to another is by radiation. Radiation can heat up a body even if it is under vacuum. Radiant heat is said to be carried by electromagnetic waves which will travel through space in straight lines at the speed of light. The heat from the sun travels to the earth's atmosphere through the vacuum in the outer space by radiation. The heat felt from a camp fire by a camper is also by radiation. Since radiant heat travels in straight lines, the camper will feel colder on the side away from the fire. /
Factors Affecting Heat Transfer
The principal factors affecting heat transfers are a) temperature difference, b) thermal resistance, c) thickness of scale and films on the heat transfer surface, d) velocity of hot and cold fluids.
Heat Exchange
The efficient use of heat in the refinery Is achieved by an equipment commonly called heat exchanger.
Heat exchangers are made in many designs and they do a variety of jobs. They can be classified as follows:
I. Coolers and condensers 2. Heaters and reboilers 3. Heat exchangers (oil to oil)
Coolers generally have water flowing through the tubes which reduces the temperature of the oil by removing sensible heat. Air coolers are also used by moving air with fans over the tubes containing oil. Condensers work the same Way except that the vapours entering the condenser change the state to liquid by removal of latent heat of condensation. Heaters usually have steam on the inside of tubes which raises the temperature of cold oil outside of the tubes by providing
sensible heat. Reboilers do the same except that the oil is vapourised and the latent heat of vapourisation is also involved.
The term heat exchanger is usually used where oil is on both sides of the tubes. The objective is to use a hot oil that needs to be cooled as a source of heat to warm up the cold oil.
Fired furnaces are commonly used to heat up oil or water. The heat is transmitted to the oil or water flowing through the tubes in the furnace.
A simple example of direct heat exchange is mixing of hot and cold liquids. This is generally avoided when temperature differential is high due to the potential hazards involved.
The cooling tower used for lowering the temperature of cooling water uses a combination of convection and evaporation heat transfer. The heat transfer is direct. The cooling medium used is air. The amount of moisture air can absorb increases greatly with increase in temperature. The water is sprayed on the top section of the tower to have a good contact with air. The internals of the tower aid to keep the water in small drops. In a spray the convection is taking place between air and water. Heat is also dissipated through evaporacion thereby cooling the water.
Heat Transfer Coefficients
Heat transfer coefficient is a means of evaluating the performance of an exchanger. This indicates the amount of heat an exchanger can interchange during a given period of time for a given surface area with a given temperature difference between the hot and cold fluids. For exchangers in operation the heat transfer coefficient helps to determine whether a heat exchanger is fouled and needs cleaning.
For a particular exchanger, the area of heat transfer is fixed by the number of tubes and the size of tubes, the temperature of the hot liquid is fairly fixed due to operating conditions. Therefore, if the heat transfer coefficient drops, then it is due to the fouling of the exchanger.
The principal factors affecting the heat exchange in an exchanger are a) the area of surface available for heat transfer, b) temperature difference between hot and cold liquid, c) velocity of the hot and cold fluids and d) thickness of scale and films on the heat transfer surfaces.
The surface area is determined by the number of tubes and the tube diameter. Usually it is a practice to minimise the diameter of the tubes consistant with the flow requirement and pressure available so as to have maximum heat transfer area for a given cross sectional area of the exchanger. The greater the area, the more heat can be transferred.
Temperature difference is the driving force to make the heat transfer, the greater the temperature difference, the greater the heat transfer will be. In order to take full advantage of the temperature difference, the hot and cold streams are designed to flow in the opposite direction.
Velocity affects heat transfer because the faster the fluid flows, the thinner is the stagnant film dragging on the wall of the tubes. The stagnant film is the result of the property of adhesion of liquids. This film offers resistance to the flow of heat and therefore reducing the thickness of this film better heat transfer results. Smaller diameter tubes reduce the film thickness by increasing the velocity.
The thermal resistance offered by scale formation affects the heat transfer. This is termed as fouling. Thermal conductivity of the scaling substances are usually very low. Scales are often formed in working units by the nature of process and can cause unit shut down due to reduced heat transfer.
The accompanying illustration shows the effect of scales and stagnant film in a heat exchanger.
Stagnant Film Scale

Tube Wall Stagnant Film
The flow of heat from a higher temperature t| to the lower temperature Ti decreases due to the resistance offered by tube side stagnant film, tube side scale, shell side scale and shell side stagnant film. The temperature drop is the greatest through the stagnant film and scale as they offer the greatest thermal resistance. The tube wall itself offers resistance which is minimized in an exchanger by using thinnest possible tube and from metals that are good conductors of heat. The effect of all thermal resistance are gathered into one mathematical term denoted as U.
The total amount of heat transferred in a given time in an exchanger can be expressed as follows:—
Q = UADT where Q = Quantity of heat transferred
U = the heat transfer coefficient
DT = The temperature difference between the hot and cold liquid
A = the total surface area of the exchanger.