![]()
UNIVERSIDAD YACAMBU
ESTADÍSTICA DESCRIPTIVA
Profesor: Sandy Quintero
Alumno: Aldo Méndez
![]()
ESPERANZA MATEMÁTICA
Investigación en Internet
VALOR ESPERADO (ESPERANZA MATEMÁTICA) DE SUMAS DE VARIABLES ALEATORIAS
La versión de la preposición del valor esperado de sumas de variables aleatorias para dos dimensiones establece que si X y Y son dos variables aleatorias, y g es una función de dos variables, entonces
E[g(X,Y) ] = å å g(x,y)p(x,y) en el caso discreto
y x
= g (x,y) ¦ (x,y) dx dy en el caso continuo
Por ejemplo, si (X,Y) = X+Y, entonces en el caso continuo 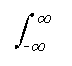

E[X+Y ] = ( (x+y )¦ (x+y) dx dy
= 

 x¦
(x,y)
dx dy +
x¦
(x,y)
dx dy + 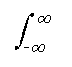
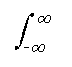 y¦
(x,y) dx dy
y¦
(x,y) dx dy
= E [X ] + E [Y ]
Un resultado se puede mostrar en el caso discreto y, desde luego, para todo par de variables aleatorias X y Y,
E [X + Y ] = E [X ] + E [Y ]
Aplicando la ecuación de valor esperado de sumas de variables aleatorias, se demuestra que el valor esperado de la suma de cualquier número de variables aleatorias es igual a la suma de sus esperanzas individuales. Por ejemplo
E [X + Y + Z ] = E [(X + Y) + Z ]
= E [X + Y ] + E [Z ] por la ecuación de valor esperado de sumas de variables aleatorias
= E [X ] + E [Y ] + E [Z ] otra vez por la misma ecuación
y en general para toda n,
E [ X1 + X2.........+ Xn] = E [X1 ] + E [X2 ] + .............. + E [Xn ] corolario (deducción demostrada anteriormente)
Esta ecuación es una formula extremadamente útil, que demuestra la deducción de la ecuación de valor esperado y la cual aplicaremos en una serie de ejemplos los cuales formularemos a continuación:
Una empresa de construcción envió recientemente tres propuestas para trabajos con ganancias de 10, 20 y 30 (miles) de dólares. Si las probabilidades de obtener el trabajo son, respectivamente, .2, .8 y .3, ¿cual es la ganancia total que espera la empresa?
Solución
Si denotamos con Xni = 1, 2, 3 la ganancia de la firma en el proyecto i, entonces tomamos:
ganancia total = X1 + X2 + X3
por ende E [ ganancia total ] = E [X1 ] + E [X2 ] + E [X3 ]
ahora E [X1 ] = 10(.2) + 0(.8) = 2
E [X2 ] = 20(.8) + 0(.2) = 16
E [X3 ] = 40(.3) + 0(.7) = 12
se suman los resultados, y así obtenemos la ganancia total que espera la empresa la cual es de 30.000 dólares.
Ejemplo 2
Una secretaria ha escrito N cartas junto con sus sobres respectivos. Pero se le caen los sobres al suelo y se le revuelven. Si se meten las cartas en los sobres revueltos de forma completamente aleatoria (es decir, cada una de las cartas tiene la misma posibilidad de meterse en cualquiera de los sobres), ¿cuál es el número esperado de cartas que se colocaran en el sobre que le corresponde?
Solución:
Al denotar X al número de cartas que se meten en el sobre que les corresponde, fácilmente podemos calcular E[X ] y observaremos que:
X = X1 + X2 + ......+ Xn
donde tenemos que
1 si la i-ésima carta se coloca en el sobre que le corresponde
X =
0 de otra manera
Ahora como la i-ésima carta tiene las mismas posibilidades de colocarse en cualquiera de los N sobres, tenemos que
P(Xi = 1) = P ( la i-ésima carta está en su sobre correspondiente) = 1/N
con lo que E [Xi ] = 1P(Xi = 1) + 0P(Xi = 0) = 1/N
por lo que con la ecuación de valor esperado el resultado es el siguiente
E [X ] = E [Xi ] + ....+ E [Xn ] = (1/N) N = 1
de esta manera no importa cuántas cartas haya en promedio, exactamente una de las cartas se meterá en el sobre que le corresponde.
|
1.- http://www.utdt.edu/~mrozada/mfin/pye2.pdf ESPERANZA MATEMÁTICA, MEDIA Y VARIANZA. La esperanza matemática de la variable aleatoria X es conocida como el primer momento de la distribución alrededor del origen. Se denota por E (X) ó ?y es un promedio ponderado de X, con ponderaciones correspondientes a las probabilidades de ocurrencia. Por ejemplo, para una variable aleatoria discreta: n E (X)= ∑ xi(xi)i=1 Donde f(x) es la función de probabilidad. En general se puede calcular la esperanza matemática de cualquier función de una variable aleatoria. Esto es: n E (g(X))= ∑ g (xi )(xi) i=1 |
||||||||||||||
|
2.- http://es.wikipedia.org/wiki/Valor_esperado Valor esperadoEn estadística el valor esperado o esperanza matemática (o simplemente esperanza) de una variable aleatoria es la suma de la probabilidad de cada suceso multiplicado por su valor. Por ejemplo en un juego de azar el valor esperado es el beneficio medio. Si todos los sucesos son de igual probabilidad la esperanza es la media aritmética. |
||||||||||||||
|
3.- http://w3.mor.itesm.mx/~cmendoza/ma835/ma83511.html VALORES ESPERADOS.Hay un par de cantidades importantes asociadas con cada variable aleatoria:
Ambas cantidades se definen en base a un operador que llamamos el operador esperanza. Matemáticamente la esperanza se define así, para una v.a. discreta E(g(X)) = suma{g(i) f(i)} donde g(i) es cualquier función y f(i) es la función de probabilidad de la v.a.; f(i) = P(X = i). Por ejemplo,
E(52X) = suma{52i f(i)} = 52 suma{i f(i)} = 52 E(X)
E( [X - 4]2 ) = suma{[i-4]2f(i)}
=
E( X/ 28) = suma{i/ 28 f(i)} = 1/28 suma{i
f(i)} = Utilizando el operador esperanza, definimos para cualquier v.a. discreta X :
|
||||||||||||||
|
4.- http://www.monografias.com/trabajos20/estadistica/estadistica.shtml ESPERANZA MATEMÁTICA También se le llama valor esperado de la distribución. Es el valor central sobre el que se concentra la distribución de probabilidad. Es semejante a la media de una distribución de frecuencias. Dada una v.a. X, definimos su esperanza como: å x i · P( x i ) " i si la v.a. es discreta E ( X ) = x · f( x ) dx si la v.a. es continua Sirve para saber las posibles ganancias o pérdidas en los juegos de azar. Se dice que un juego es justo cuando la esperanza es cero.
A partir de la esperanza de la v.a. X, se puede obtener su varianza: Var( X ) = E( X 2 ) - [ E( X ) ]2 EJEMPLO Calcular la esperanza y la varianza de una v.a. continua con función de densidad : _1_ si x Î (0, 1) 2 f( x ) = 0 si x Ï (0, 1) Solución : E ( X ) = x · f( x ) dx = _x_ dx = _1_ 2 x 3
E ( X 2) = x2 · f( x ) dx = _x2_ dx = _1_ 2 x 5
Var ( X ) = E ( X 2) [ E ( X ) ] 2 = _1_ _ _1_ 2 = _4_ 5 3 45
|
||||||||||||||
|
5.- http://faea.uncoma.edu.ar/materias/estadistica_cont/documentos/4._Mod_Discretos.pdf ESPERANZA MATEMÁTICADefiniciónEl valor esperado o esperanza matemática de una variable aleatoria X es un promedio ponderado de los valores que puede asumir X con probabilidades para los valores de X como pesos; es decir es un promedio ponderado; es representado por E(X). EX caso discreto xpxii)in().(==.1 Propiedades de la esperanza matemática:1.- E( k )= k , siendo k una constante 2.- E(X + k ) = E( X) + k 3.- E( k. X ) = k E(X) 4.- E(XアY ) = E(X) ア E(Y) 5.- E(X . Y ) = E(X) . E(Y) . X e Y son variables independientes. |
||||||||||||||
|
6.- http://www.aeatonline.com/racionalidad/hbiba11.html Esperanza Matemática La única condición indispensable para validar un método de inversión es que la esperanza matemática de su resultado (neto de gastos y penalizaciones por liquidez) sea positiva : (Resultado> 0).
Resultado =
esperanza matemática del resultado Resultado = 0.4 * .03 + 0.6 * (-0.015) = 0.003 > 0
En este caso, aun siendo menos
probables las operaciones positivas que las negativas (40%<60%) el resultado
esperado es positivo. |
||||||||||||||
|
EJEMPLOS DE ESPERANZA MATEMÁTICA |
||||||||||||||
|
7.- http://ftp.medprev.uma.es/libro/node61.htm Valor esperado o esperanza matemáticaSea X una v.a. discreta. Se denomina esperanza matemática de X o valor esperado, y se denota bien o E [X ] bien , µ a la cantidad que se expresa como:
E [X ] = Σ Xi (Xi)
iЄII donde II = {1,2,...,k} para un número finito de valores de la v.a. o bien II = IN para una cantidad infinita numerable de los mismos.
Si X es una v.a. continua, se define su esperanza a partir de la función de densidad como sigue:
+∞ E [X] = ∫ x. (x) dx -∞
Recordamos que si
X : E → IR ==> h (X) = h o X : E → IR es variable aleatoria h : IR→ IR
y por tanto tiene sentido calcular su esperanza matemática:
+∞ E [h(X)] = ∫ h(x). (x) dx -∞
Por las analogías existente entre la definición de media aritmética y esperanza matemática, las propiedades de linealidad de la primera se trasladan a la segunda, como es inmediato comprobar:
E [a + b . X ] = a + b . E [ X ]
E [X - E[ X ] ] =
E [ X ] - E [ X ] = 0
|
||||||||||||||
|
8.- http://www.itchihuahuaii.edu.mx/academico/CB/MEG/documentos/1.2.htm ESPERANZA MATEMÁTICA O VALOR ESPERADO Sea F(x) una variable aleatoria discreta con función de probabilidad P(X=Xi). Entonces al valor esperado o esperanza matemática de F(x) está definida por: E {F(X)} = F(X) P(X=Xi) Calcule la media y la varianza con la esperanza matemática de los puntos mostrados cuando se lanza un dado.
F(X) = X
µ= E {X} =
µ = E { X } = 1 ( 1/6) + 2 ( 1/6) + 3 (1/6) + 4 ( 1/6) + 5 (1/6) + 6 (1/6 ) = 3.5
(5 - 3.5 )2 (1/6) + (6 - 3.5 )2 (1/6) = 2.91
|
||||||||||||||
|
Esperanza Matemática Se llama esperanza matemática de una variable aleatoria X, E(X), al valor real que representa el promedio de X dado por: . ?= k k p x X E ) ( si X es discreta . ?= dx x f x X E ) ( ) ( si X es continua donde ) ( k k x X P p = = y ) (x f son las funciones de probabilidad y de densidad, respectivamente. La sumatoria y la integral se extienden a todos los valores de la v.a. X. Si X es una variable aleatoria, entonces g(X) será también otra variable aleatoria y se define la esperanza de g(X) como: [ ] . ?= k k p x g X g E ) ( ) ( si X es discreta [ ] . ?= dx x f x g X g E ) ( ) ( ) ( si X es continua |
||||||||||||||
|
10.- http://www.bioestadistica.uma.es/libro/node98.htm Estimador de la esperanza matemáticaEstimador de la esperanza matemáticaConsideremos las muestras de tamaño n, X1, X2 ...,Xn de un carácter sobre una población que viene expresado a través de una v.a. X que posee momentos de primer y segundo orden, es decir, existen y E [X ] Var [X ] E [Xi] =µ X1, X2 ...,Xn Var [Xi] = 0-2 El estimador muestral que denotaremos como X (en lugar de µ es X = 1/n (X1 + X2 + ...+Xn)
|
