Background to Classification and Clustering
Most research is concerned with identifying the 'rules' which control processes that interest us. Assuming that these rules exist, the aim of the researcher is to derive them from the available evidence. The starting point is a statement of the problem, which might be expressed as a theory or as a question. For example:
- Increasing call complexity in corncrakes is related to breeding success. (a theory)
- Is migraine frequency related to light intensity? (a question)
- Is blood pressure related to salt intake? (a question)
- Is species diversity related to habitat complexity? (a question)
Answering the question or finding evidence in support of the theory requires some new information, which can be derived in a number of ways.
- From observations of 'natural' processes (induction). This is equivalent to being a detective, what can you conclude from the available evidence? You can probably rule out some explanations ('suspects'), but others may be more difficult to eliminate. Induction is recognising the general from the particular ('seeing the woods through the trees'), this involves finding and explaining patterns in the data.
- From controlled experiments that are designed to differentiate between the possible explanations of the observed phenomenon using deduction. Deduction differs from induction because it depends on having access to previous knowledge. In fact the conclusion is inevitable given the premises. In general induction from observation precedes deduction from experimentation.
The balance between induction and deduction varies between different branches of science and the position in the research cycle. For example, astronomers find it difficult to carry out controlled experiments, similarly it is often difficult to undertake controlled ecological experiments. It is quite common to use 'natural experiments' as a means of obtaining data that can be analysed and used to generate hypotheses, prior to designing more powerful experiments that can test the hypotheses.
Even if experiments are difficult it is still possible to make a prediction prior to collecting any data. You can then see if the data support the theory. Although agreement is not conclusive, lack of agreement would be strong evidence against the theory. Evidence for or against the theory is contained within the data collected. However, data is not information. Information is data with 'added value'. The added value comes from an appropriate analysis of the data.
Because biological processes are rarely simple, it is normally impossible to derive simple rules like Boyle's law. The problem is often one of separating the 'signal' from the 'noise'; some biological systems are very noisy.
When we collect data we hope that they contain some signals and not too much noise. The example above shows three xy plots that have the same relationship between x and y (regression line slope), but different amounts of noise. The relationship between the two varaibles is the signal.
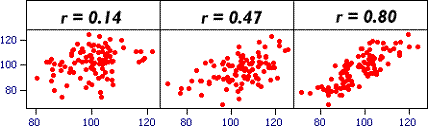
1 |
Signal and NoiseThese statements relate to the three scatter plots above. Identify which are valid. |
Our role, as data analyst, is to find the signal and demonstrate, if possible, that it isn't spurious. Unfortunately, this becomes increasingly more difficult as the volume of data increases, if only because spurious correlations, etc, are more likely as more relationships are examined.
2 |
Type I errorsThe chance of finding a statistically significant spurious, i.e. not a real, relationship is the same as the level of statistical significance. |
It is worth remembering that not all data contain messages. Consider Pi, an irrational number with an infinite number of decimal places. Pi to 50 decimal places is 3.4159265358979323846264338327950288419716939937510....... Despite what some people think there is no hidden message in these data. There is no pattern or message from the gods. The take home message is that data don't always contain signals, even though they may have cost a fortune to collect.
In this unit the focus is on finding patterns in data that enable cases to be placed into groups. This is achieved using clustering and classification algorithms. These techniques share many similarities in that they exploit the similarities between cases. The difference is that classification is essentially concerned with allocating cases to pre-defined groups, while clustering is concerned with finding groups in heterogeneous collections of cases.
A common starting point for all clustering and classification algorithms is a table in which rows represent cases (instances) and columns are the variables. Once they are in this format their original source, for example microarrays, quadrats, etc, is largely irrelevant. The hope is that we can find some structure (signals) in these data that enable us to test or develop biological hypotheses.
If the data contain one or more signals there will be some recognisable structure within the table. However, this structure may be masked by the current order of the rows and columns. In this simple example the only processing has been a simple reordering and the rows and columns. Life and data aren't always that simple.
| case | a | b | c | d | e | f | g | h | i |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 1 | 4 | 0 | 5 | 3 | 0 | 0 |
| 2 | 1 | 3 | 2 | 0 | 4 | 0 | 0 | 5 | 4 |
| 3 | 0 | 2 | 1 | 0 | 3 | 0 | 0 | 4 | 5 |
| 4 | 2 | 4 | 3 | 0 | 5 | 0 | 1 | 4 | 3 |
| 5 | 4 | 4 | 5 | 2 | 3 | 1 | 3 | 2 | 1 |
| 6 | 3 | 5 | 4 | 1 | 4 | 0 | 2 | 3 | 2 |
| 7 | 3 | 1 | 2 | 5 | 0 | 4 | 4 | 0 | 0 |
| 8 | 4 | 2 | 3 | 4 | 1 | 3 | 5 | 0 | 0 |
| 9 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 3 | 4 |
| 10 | 5 | 3 | 4 | 3 | 2 | 2 | 4 | 1 | 0 |
If the rows are columns and re-ordered, as shown below, the following structure appears.
| case | f | d | g | a | c | b | e | h | i |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 | 0 |
| 8 | 4 | 5 | 4 | 3 | 2 | 1 | 0 | 0 | 0 |
| 9 | 3 | 4 | 5 | 4 | 3 | 2 | 1 | 0 | 0 |
| 7 | 2 | 3 | 4 | 5 | 4 | 3 | 2 | 1 | 0 |
| 5 | 1 | 2 | 3 | 4 | 5 | 4 | 3 | 2 | 1 |
| 6 | 0 | 1 | 2 | 3 | 4 | 5 | 4 | 3 | 2 |
| 2 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 4 | 3 |
| 3 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 4 |
| 10 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 4 | 0 | 0 | 0 | 0 | 0 | 1 | 2 | 3 | 4 |

