Main: The Wave equation

An alternative derivation of the 1D Green's function

Consider the Green's function for the one space dimension wave equation;

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {t}^2}}-{{\partial^2 G}\over{\partial {x}^2}} = \delta(x-y)\delta(t-\tau). \end{displaymath}$

If we put z=x-y and 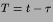$T=t-\tau$ this becomes

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {T}^2}}-{{\partial^2 G}\over{\partial {z}^2}} = \delta(z)\delta(T). \end{displaymath}$

We want the solution G(z,T) which has outgoing wave behaviour, that is, the solution for which waves move outwards from z=0 towards infinity (as opposed to waves that move inwards from 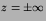$z=\pm\infty$ towards z=0).

Ignoring the 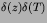$\delta(z)\delta(T)$ term (which is only nonzero if z=0 and T=0) the d'Alembert solution can be written as

$\begin{displaymath} G(z,T) = \hat{F}(T-z/c) + \hat{E}(T+z/c) \end{displaymath}$

where

$\begin{displaymath} \hat{F}(T-z/c) \end{displaymath}$

represents a wave travelling away from z=0 towards $z=\infty$ and

$\begin{displaymath} \hat{E}(T+z/c) \end{displaymath}$

represents a wave travelling towards z=0 from 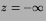$z=-\infty$ . If we want a wave that travels away from its source, at z=0, then for z>0 we need the wave moving away from z=0 towards $z=\infty$ , that is

$\begin{displaymath} \hat{F}(T-z/c) \end{displaymath}$

and for z<0 we need the wave moving away from z=0 towards 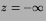$z=-\infty$ , that is

$\begin{displaymath} \hat{E}(T+z/c). \end{displaymath}$

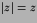Now observe that $\left\vert z\right\vert = z$ for z>0, and the appropriate wave behaviour is (for z>0)

$\begin{displaymath} \hat{F}(T-\left\vert z\right\vert/c) \end{displaymath}$

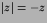and for z<0, $\left\vert z\right\vert = -z$ and the appropriate wave behaviour is (for z<0)

$\begin{displaymath} \hat{E}(T+z/c) = \hat{E}(T-\left\vert z\right\vert/c) \end{displaymath}$

Thus, to get outgoing wave behaviour we want a solution of the form

$\begin{displaymath} F(T-\left\vert z\right\vert/c). \end{displaymath}$

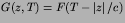Now substitute $G(z,T) = F(T-\left\vert z\right\vert/c)$ into

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {T}^2}}-{{\partial^2 G}\over{\partial {z}^2}} = \delta(z)\delta(T). \end{displaymath}$

Then

$\begin{displaymath} {1\over c^{2}} {{\partial^2 G}\over{\partial {t}^2}} = {1\over c^{2}} F''(T-\left\vert z\right\vert/c) \end{displaymath}$

and

$\begin{displaymath} {{\partial G}\over{\partial x}} = -{\hbox{sgn}(z)\over c} F' (T-\left\vert z\right\vert/c) \end{displaymath}$

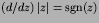since $(d/dz)\left\vert z\right\vert=\hbox{sgn}(z)$ (see Chapter 1). Thus

$\begin{displaymath} {{\partial^2 G}\over{\partial {x}^2}} = -{2\delta(z)\over c... ...ox{sgn}(z)\over c\right)^{2} F''(T-\left\vert z\right\vert/c) \end{displaymath}$

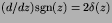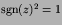since $(d/dz)\hbox{sgn}(z) = 2\delta(z)$ (again, see Chapter1). Since $\hbox{sgn}(z)^{2}=1$ whatever z is and 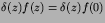$\delta(z)f(z)=\delta(z)f(0)$ this becomes

$\begin{displaymath} {{\partial^2 G}\over{\partial {x}^2}} = -{2\delta(z)\over c} F'(T) + {1\over c^{2}} F''(T-\left\vert z\right\vert/c). \end{displaymath}$

Hence

$\begin{displaymath} {1\over c^{2}}{{\partial^2 G}\over{\partial {T}^2}} - {{\... ...rtial {z}^2}} = {2\delta(z)\over c} F'(T) = \delta(z)\delta(T) \end{displaymath}$

so that

$\begin{displaymath} F'(T) = {c\over 2}\delta(T) \end{displaymath}$

and hence

$\begin{displaymath} F(T) = {c\over 2}H(T). \end{displaymath}$

Thus

$\begin{displaymath} G(z,T) = F(T-\left\vert z\right\vert/c) = {c\over 2} H(T-\left\vert z\right\vert/c) \end{displaymath}$

so that

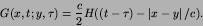$\begin{displaymath} G(x,t; y,\tau) = {c\over 2} H( (t-\tau) - \left\vert x-y\right\vert/c). \end{displaymath}$

(47)

Main: The Wave equation

Hosted by www.Geocities.ws