Square 1

A Rubik's Cube on Acid

"Ohhh... I'm sooooo wasted!"

Transform the Puzzle into a Cube

Step I: Get the puzzle into 3 distinct layers

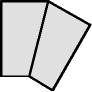
Square 1 is a mixture of small wedges, large wedges, and two trapezoids. The two trapezoids belong in the equator (middle layer) of the puzzle, and must be joined together:

like this:

or like that:

Once the trapezoids are joined together, the puzzle is automatically at 3 distinct layers. This is way too easy, for two reasons:

• No matter how badly the puzzle is scrambled, you are (at the most) only ONE move away from getting there.
• At that point, it was the ONLY move you could have made here anyway!

---

Step II: Try to fill one layer with 6 large wedges

Once the puzzle is at 3 distinct layers, it can appear as one of many (90, to be exact) geometric shapes. There are just too many permutations to memorize, so the easiest way I can think of is to follow this simple rule:

Fill an outside layer (top or bottom) with 6 large wedges. This will force the other side to have 2 large wedges and 8 small wedges. There are only 5 possible combinations for that mixture, therefore there will be only 5 tranformations to memorize afterwards.

This is not as hard as you think, but if you are still having trouble then I suggest you visit...

Christian Eggermont's Square 1 Page

...where you can start from any absurd shape to the final cube, one step at a time. The charts do not expect you to memorize the steps, but will help you get through that first obstacle. Besides, the geometric shapes are rather beautiful to look at.

As you become more familiar with and accustomed to the puzzle, then you will find it easier to get six large wedges on one layer all by yourself without the charts, and all you really had to do was play around with it for a few days. The key is to get three large wedges next to each other on both layers. Here is one example:

Note: There is no need to memorize the above table; it is merely an example.

Step III: Transform the puzzle into a cube

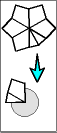
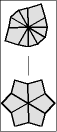
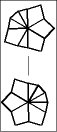
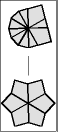
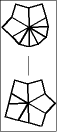
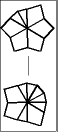
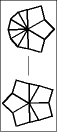
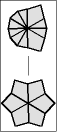
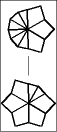
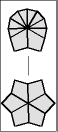
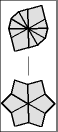
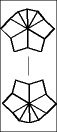
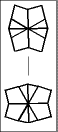
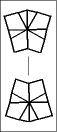
Once one layer is filled with 6 large wedges, then it is time to memorize the chart below to transform the puzzle to its final shape, the CUBE; or at least practice it enough so it becomes second nature.

The 5 possible starting postions are shaded in gray. Find your pole position and follow the arrows until you arrive at the finish line. To make a move, start off by setting the top and bottom layers just like one of the diagrams, then give the entire right side a twist. After that, turn the top and/or bottom layer so that they match the next diagram, before doing the twist again.

...and if the equator still needs fixing...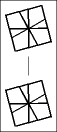

NOTE: the gap between the layers represents the front edge;
i.e., the front edge of the top layer points down,
the front edge of the bottom layer points up,
and finally, the "line-thingy" in the middle is the "slice" in the equator.

Notation

There are two different types of notation here. The first is what I call Descriptive Notation, which seems to be the accepted notation in most Square-1 web sites, so there is no sense for me to invent yet another one. The other was created by Jaap Scherphuis, which I prefer mainly because of its clarity and simplicity. Besides, it's a lot easier to type! Anyway, you only need to choose one of them.

Basically you get the idea: t for top and b for bottom; plus for clockwise and minus for counter-clockwise, followed by the number of increments (1,2,3... etc.); and finally R for turning the right side. When using the JS notation, you can combine both top and bottom moves within a single set of parenthesis. To learn more about Jaap Scherphuis' notation, I strongly suggest that you visit his Square 1 page:

Jaap's Square 1 Page

NOTE: A clockwise move for bottom layer spins in the opposite direction of a clockwise move for the top layer. Imagine holding a jar with the lid on the top. To close the jar, you must turn the lid clockwise, twisting it to the left. Now imagine holding a jar upside-down. To close the same jar, you must also turn the lid clockwise, but now it twists to the right instead.

NOTE continued: The same goes for the counter-clockwise move; as they also spin in opposite directions for both top and bottom layers. To remove the lid, you must turn it counter-clockwise. If you are holding the jar right-side-up, then you must twist to the right. If you are holding the jar upside-down, then you must twist to the left.

I know this is all very confusing, but just pretend that for every clockwise move, you're screwing a lightbulb in; and for every counter-clockwise move, you're unscrewing a lightbulb out.

Because the Square 1 puzzle has a tendency to mutate into so many bizzare shapes, I will try to keep things as orthogonal as possible; in other words, I almost promise to keep the top and bottom layers square throughout the solution. I also almost promise to keep each move itself at right-angle increments, with the minor exception of the +1 or -1 moves that lead and trail for each sequence.

The First Sequence

Once the puzzle is transformed into a cube, you only have to memorize ten sequences to solve the colors, starting right NOW...

Fix the equator:

Now that we are aquainted with the notation, it is time to learn your first lesson by solving the equator.

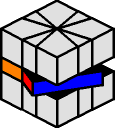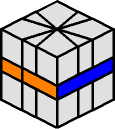				Desc. notation:		JS notation:
				b- R t6 R t6 R b+		(0,-1)/(6,0)/(6,0)/(0,1)

This is probably the most important move to memorize, as there will be times when the equator accidentally gets out of shape. After the move is over, the equator is square again, and the top and bottom layers are left exactly as they were before.

A Note of Thanks

Before we continue, I must give credit where credit is due:

First of all, many kudos go to Jaap Scherphuis for helping me polarize the cube, which you will have to do later on yourself during the course of this solution. Just as he is indebted to Robert Richter for transforming the puzzle into cube, I feel equally indebted to him for teaching me how to get the the puzzle from odd parity to even parity. In the meantime, you should seriously consider visiting his home page; the single most comprehensive puzzle site on the web:

Jaap's Puzzle Page

Another round of applause goes to Christian Eggermont, the web-site that started it all! A decade ago, this was the only puzzle site available at the web. Today, it is still considered as the mecca for many cubists:

Christian Eggermont's Puzzle Page

NEXT: Solve the Top Corners

@ Transformation @ Top Corners @ Bottom Corners
@ Top Edges @ Polarization @ Bottom Edges

Return to Mathematica

Hosted by www.Geocities.ws