

During this section, you must memorize 2 more moves; the POLARIZING sequence and the FIXING sequence.
First of all, many thanks to Jaap Scherphuis for helping me out through these tough times of polarization, parity, and (what HE calls) permutations concepts. Just as he is indebted to Robert Richter for transforming the puzzle into cube, I feel equally indebted to him for teaching me how to easily permutate the puzzle from odd to even. Who knows? Maybe Square-1 is the only puzzle that was solved via the world-wide-web. To learn more about Jaap Scherphuis' theories, I strongly suggest that you visit his web site (the most comprehensible puzzle site on the 'net):
Jaap's Puzzle Page
Jaap's Square 1 Page
On the Rubik's Cube, it is impossible for a single pair of edges to become swapped . However, on Square 1, it is indeed possible for this to happen. If only a single pair of edges need swapped, then puzzle is at ODD parity; ...EVEN parity is when two edge pairs need swapped. The move currently used to solve the bottom edges can only handle cubes at even parity, so the answer is to convert the parity from ODD to EVEN. I call it polarizing, but you can call it anything you want.
You have to polarize your puzzle if and only if the parity is odd. The next question is:
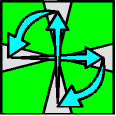
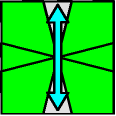
Assuming that the top layer and bottom corners are finished, the clue lies in the unfinished bottom edges. Look at the bottom side; there are 10 total possibilities...
 |  |  |  |
|||
| Parity = 2 | Parity = 2 | Parity = 2 | Parity = 2 |
As you can see, parity has nothing to do with how many edges are scrambled, but instead how many edge pairs are swapped. If the bottom edges look like any of the 4 examples above, then the parity is already even; so do not by any means polarize your cube... instead, bypass this page and go directly to the next step:
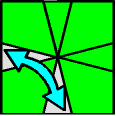 |  |  |
||
| Parity = 1 | Parity = 3 | Parity = 3 | ||
 |  | 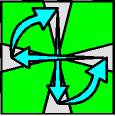 |
||
| Parity = 1 | Parity = 3 | Parity = 3 |
Once again, parity has nothing to do with how many edges are scrambled, but instead how many edge pairs are swapped. If the bottom edges look like any of the 6 examples above, then the parity is odd; which means you absolutely have to polarize your cube... so hold your breath and get ready for battle.
SET UP: Make sure that the front sides of the top and bottom corners are orange.
/ t+3 b-3 / t+2 b- / |
Click here to see the moves in graphical notation.
While you do this move, you will notice that the puzzle will morph into the bizzarre shape it was at when you took it out of the box, causing an intense experience of deja-vu. After the move, the puzzle is restored to a cube again.
Can it ever be fixed?!? As it turns out, the fix is a rather simple sequence... but before doing the next move, check and make sure that the front sides of the top layer corners are orange, while the front sides of the bottom layer corners are yellow. (Ignore the colors of the edge pieces).
b- / t+3 b-3 / b+ |
Click here to see the moves in graphical notation.
Now the top layer and bottom corners are solved again, and the cube is polarized at even parity to boot! The only pieces that are still remain scrambled are the bottom edges.
If you did the polarizing and fixing moves correctly, the top layer and bottom corners will be solved again. Only the bottom edges are still scrambled, and because the cube is now at even partity, you can go ahead and...
Note: if you screwed up somehow, you'll have to start all over again; but chances are that the cube became correctly polarized somewhere along the way, so you can probably skip this section the next time around.