Square 1

Solve the Bottom Edges

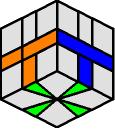
During this section, you only have to use one sequence of moves.

Only one sequence is used throughout this page, one that has already been used before; so here is the RERUN...

What we want the move to do: THE MOVE: What the move really does:
To swap a single pair
of edges on the bottom layer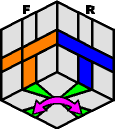

 Desc. notation:

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

JS notation:

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

It swaps the back and left
edges on the bottom layer, while
swapping the back and right
edges on the top layer.

As you can see, every time a pair of bottom edges are swapped, a pair of top edges also become swapped. Therefore, the sequence must be used again to re-fix the sacrificial top edges. The result? The edges on the bottom layer are swapped TWICE, which is why we had to polarize the cube to even parity before going ahead with this step.

You might be able to figure out how to individually swap the bottom edges until they are fixed; but just in case, a step-by-step outline was added.

~~~~ Case I ~~~~
Clockwise Exchange

SET UP:

Rotate the bottom layer so that the 3 edges
to be exchanged are on the back, left and right.
In other words, get the "other edge" at the front.
Do the move: Rotate the bottom
layer 1/4 of a turn
clockwise		 Do the move again: Result:
Desc. Notation:

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

b+3

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

 The puzzle is solved!
JS Notation:

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

(0,3)

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

~~~~ Case II ~~~~
Counter-Clockwise Exchange

SET UP:

Rotate the bottom layer so that the 3 edges
to be exchanged are on the back, left and front.
In other words, get the "other edge" at the right.
Do the move: Rotate the bottom
layer 1/4 of a turn
counter-clockwise		 Do the move again: Result:
Desc. Notation:

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

b-3

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

 The puzzle is solved!
JS Notation:

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

(0,-3)

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

~~~~ Case III ~~~~
Adjacent Edge-Pair Swap

SET UP:

Rotate the bottom layer so that two of the edges
that need to be swapped are at the back and left,
while the other two are at the front and right.
Do the move: Rotate the bottom
layer 1/2 of a turn
around		 Do the move again: Result:
Desc. Notation:

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

b6

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

 The puzzle is solved!
JS Notation:

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

(0,6)

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

~~~~ Case IV ~~~~
Opposite Edge-Pair Swap

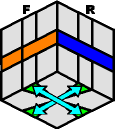SET UP:

None (don't care).
Do the move: Rotate the bottom
layer 1/4 of a turn
at any direction		 Do the move again: Result:
Desc. Notation:

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

b+3
~or~
b-3

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

 The bottom layer has 3 edges
that are still scrambled.
If they need to be
exchanged clockwise,
then go to Case I.
If they need to be exchanged
counter-clockwise,
then go to Case II.
JS Notation:

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

(0,3)
~or~
(0,-3)

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

A Shortcut for the Experts:

This sequence does the exact same thing that other sequence did, but with fewer moves. The moves are are not orthogonal, but the top and bottom layer will always remain square:

Swap the back/right edges
on the top layer, while
swapping the back/left edges
on the bottom layer:
Desc. Notation:
JS Notation:

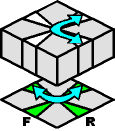b- R b-3 R b+
t+ R b+2 t- R b+

(0,-1)/(0,-3)/(1,1)
/(-1,2)/(0,1)

And now that the nightmare is finally over, you can live happily ever after.

THE END

Quick Summary of All Move Sequences:

Desc. NotationJS NotationComments

b- R t6 R t6 R b+

(0,-1)/(6,0)/(6,0)/(0,1)

Fixes the Equator

b- R t6 b6 R b+

(0,-1)/(6,6)/(0,1)

 Swaps the top and
bottom layers

t+ R b-3 R b-3 R b6 R t-

(1,0)/(0,-3)/(0,-3)/(0,6)/(-1,0)

 Moves up a single
corner to the top

t+ R b-3 R
b+3 R b-3 R
b-3 R b6 R t-

(1,0)/(0,-3)/
(0,3)/(0,-3)/
(0,-3)/(0,6)/(-1,0)

 Fixes the top corners

b- R t+3 R
t-3 R t+3 R
t+3 R t6 R b+

(0,-1)/(3,0)/
(-3,0)/(3,0)/
(3,0)/(6,0)/(0,1)

 Fixes the bottom corners

b- R b+ t+ R t-

(0,-1)/(1,1)/(-1,0)

 Places the first
two top edges

b- R b-3 R b+
t+ R t6 R t-
b- R b+3 R b+
t+ R t6 R t-

(0,-1)/(0,-3)/(1,1)/
(6,0)/(-1,-1)/(0,3)/
(1,1)/(6,0)/(-1,0)

 Places the last
two top edges

b- R b-3 R b+
t+ R b+3 R t-
b- R b+ t+ R t-

(0,-1)/(0,-3)/
(1,1)/(0,3)/
(-1,-1)/(1,1)/(-1,0)

 Fixes the top and bottom edges

R t-3 b-3 R t-2 b- R
t-2 b-2 R b-2 R t-2 b-2
R t-2 b- R t+3 b+3 R

/(-3,-3)/(-2,-1)/
(-2,-2)/(0,-2)/(-2,-2)
/(-2,-1)/(3,3)/

 Polarizing move

b- R t-3 b-3 R b+
t+ R t-3 b-3 R t+2

(0,-1)/(-3,-3)/
(1,1)/(-3,-3)/(2,0)

 Polarizing fix

@ Transformation @ Top Corners @ Bottom Corners
@ Top Edges @ Polarization @ Bottom Edges

Return to Mathematica

Hosted by www.Geocities.ws

1