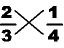
Remember way back in Elementary School, when you were forced to learn how to add fractions? Your teacher probably rambled on something like this:
"Find the least common denominator between the two fractions and multiply the appropriate number to the numerator and denominator of one fraction, while multiplying a possibly different number to the numerator and denominator of the other fraction to yield a common denominator for both fractions. Add the numerators of both fractions together to obtain the numerator of the final answer, with the denominator of the answer still being the least common denominator recently found, before reducing the fraction... etc., etc., etc."
And then you went to Junior High and finally High School, and every year during Math Class you were still forced to learn fractions, and listen to another teacher say something like:
"Find the least common denominator between the two fractions and multiply the appropriate number to the numerator and denominator of one fraction, while multiplying a possibly different number to the numerator and denominator of the other fraction to yield a common denominator for both fractions. Add the numerators of both fractions together to obtain the numerator of the final answer, with the denominator of the answer still being the least common denominator recently found, before reducing the fraction... etc., etc., etc."
There is an easier way to add fractions; I call it the "criss-cross" method. But before you begin my class, you must learn two words:
NUMERATOR: the number ABOVE the bar
DENOMINATOR: the number BELOW that same bar
Now that you're an expert on LATIN, let's move on to adding those mysterious semi-numbers we call fractions!
Draw a BIG 'X' (criss-cross) between the two fractions:
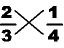
MULTIPLY the numbers of one leg of the 'X', and write the answer on top:
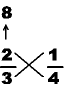
MULTIPLY the numbers of the other leg, and write that answer on the top:
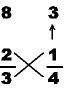
ADD those numbers together. This is the NUMERATOR:
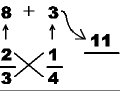
MULTIPLY the two BOTTOM numbers together. This is the DENOMINATOR:
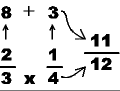
...and you're done! This does NOT guarantee that the fraction is reduced, but SO WHAT! You can always do that later. But at least you have an answer that will give you half-credit. Remember: multiply, multiply, add & multiply. Ahhhh... but you're a perfectionist and want to actually reduce that sucker. The best way to do that is to recognize if a number is divisible by other numbers, or FACTORS.
In the example above, the answer was 11/12. The fraction is already reduced, so you passed that question with flying colors. But what happens when you add 1/10 + 2/5 (using the criss-cross method)? The answer would be 25/50, which is NOT reduced, because the REAL answer is 1/2 ! The best way to reduce numbers is to recognize their FACTORS.
Multiples of 2:
Any EVEN number is a multiple of 2.
Multiples of 5 and 10:
Any number ending with a '0' is a multiple of 10. Any number ending with either '0' or '5' is a multiple of 5. So far, so good. Is this way too easy, or what?
Multiples of 3, 6 and 9:
Take any number, and add the INDIVIDUAL digits together. For example:
864
8 + 6 + 4 = 18
...and keep adding those individual digits together until you get a SINGLE number:
1 + 8 = 9
If the final answer is 9, then the ORIGINAL number is a multiple of 9.
If the final answer is 3, 6 or 9, then the ORIGINAL number is a multiple of 3.
If the answer is 3, 6 or 9; and if the original number is EVEN, then the ORIGINAL number is divisible by 6.
In this case, the number 864 is multiple of (or "divisible by") 3, 6 AND 9.
Multiples of 4:
In this case, You only have to pay attention to the LAST TWO DIGITS. First of all, in order for a number to be divisible by 4, the original number has to be EVEN.
1,197,532
...okay, it's EVEN. Now for the SECOND test. Look at the last two numbers (only):
32
DIVIDE the LAST number by 2:
2 / 2 = 1
...and ADD it to the OTHER number:
1 + 3 = 4
If the final answer is EVEN (like in our carefully selected example), then the ORIGINAL number is a multiple of 4. But wait, this method had TOO MANY STEPS! It was also a little confusing. Is there an EASIER way? Yes! And that way is simply; if the last TWO digits of ANY number is a multiple of 4, then the ENTIRE number is divisible by 4. You may have to use long division to find this out, but at least you only have to work on a 2-digit number. In this case, the number 1,197,532 is multiple by 4 simply because 32 is also a multiple of 4.
Multiples of 8:
If the last THREE digits of ANY number is a multiple of 8, then the ENTIRE number is divisible by 8. For example, the number:
2,357,111,317,192,329,312
...is divisible by 8 simply because 312 is also divisible by 8.
Multiples of 7:
Enter the number in your calculator. Divide it by 7. If the answer is an integer, then the number is divisible by 7. Okay, so I'm a sarcastic cynic. Vignettes!
But there is a certain method you can use to find out if a number is divisible by 7. Maybe not so quick, and somewhat mechanical, but still rather clever:
Example:
3535
Split off the LAST digit away from the rest of a number:
353 | 5
Double that digit, and subtract it from the REST:
353 - 10 = 343
Keep repeating until you only have 1 or 2 digits left:
34 | 3
34 - 6 = 28
If the answer is a basic multiple of 7 (0, 7, 14, 21, 28, 35, etc.), then the entire original number itself is also a muliple of 7.
Multiples of 11:
This is a real ACID TEST of our pathetic abilities. You may be better off just doing this thing by hand, but anyway; there is a "shortcut", even though in reality it's a bit of a stretch:
142,857
Take the 1st, 3rd, 5th, etc., digits and add them together:
1 + 2 + 5 = 8
Now take the 2nd, 4th, 6th, etc., digits together and add those together:
4 + 8 + 7 = 19
Subtract the two "new numbers":
19 - 8 = 11
If the answer is an obvious multiple of 11 (0, 11, 22, 33, etc.) then the ORIGINAL number is a multiple of 11, just like in our example.