

These are examples of Binary Wheels. On the left, there are actually 4 binary wheels. They are concentric only for the sole reason of saving space. The inner-most wheel is what I call a 3-BIT WHEEL. If you mask off all but 3 of the dots, you will see a 3-dot pattern through the window that represents a 3-bit binary number (black=1, white=0). As you move the window around the wheel, you will be able to view all 8 Octal numbers in binary format.
So what? Well, think of this: it takes 24 bits of information to represent all 8 Octal numbers (8x3 bits). By using a binary wheel, you only need 8 since they overlap each other. The only drawback is the fact that the Octal numbers will not ascend in order as you increment the window clockwise dot-by-dot; sort of like a new Gray Binary System.
A mathematical breakthrough? No, because you are really not saving information. You still need to specify 8 positions to navigate the window around the wheel, and that specification will eat up those 16 bits you thought you were saving, plus more bits to translate the psuedo-Gray code. But the idea is still kind of neat.
The next-outer wheel is a 4-bit wheel. In this case, you mask off all but FOUR dots, and can view all 16 Hexadecimal numbers through the window as you scroll around the wheel. Once again, only 16 bits are used to represent 48 bits of information. The next outer wheel is for 5-bit binary numbers, and the outer-most wheel is for the 6-bit type.
On the right is a single wheel with two rows. If you mask off all but a 3x2 section of dots, you will be able to view all 64 Braille charcters through the window as you scroll around.
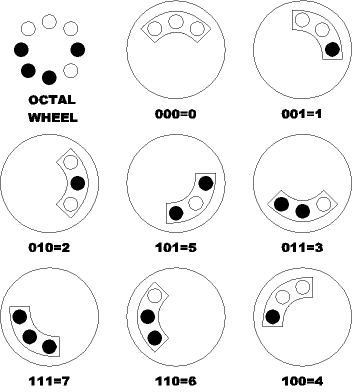
How the 3-bit wheel displays all 8 octal codes.