Sistema vigesimal

El sistema de numeración Maya era vigesimal, basado en el número 20, en vez de la base 10 usada actualmente.

En este último sistema hay diez cifras diferentes, 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 que se usan para representar cualquier número como potencias de la base del sistema, el número 10. Por ejemplo, el número 258 significa 2 x 10² + 5 x 10¹ + 8 x 10⁰, es decir, dos centenas más cinco decenas más 8 unidades.

La notación en el sistema vigesimal es similar salvo que la base es 20. En este sistema se necesitan veinte cifras diferentes, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, y 19 que también se pueden representar como 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I y J. El número 6HF ó 6.17.15 significa, desde el punto de vista decimal 6 x 20² + 17 x 20¹ + 15 x 20⁰ = 2755.

Según la posición las sucesivas cifras de cada número en el sistema decimal representan unidades, decenas, centenas, unidades de millar, etc; en el sistema vigesimal los nombres eran kines, uinales, tunes, etc. En la siguiente tabla se muestran algunos de los nombres:

Sistema decimal, base 10		Sistema vigesimal, base 20
Unidades	100 = 1	Kines	200 = 1
Decenas	101 = 10	Uinales	201 = 20
Centenas	102 = 100	Tunes	202 = 400
Unidades de millar	103 = 1000	Katunes	203 = 8000
Decenas de millar	104 = 10000	Baktunes	204 = 160000
Centenas de millar	105 = 100000	Pictunes	205 = 3200000
Unidades de millón	106 = 1000000	Calabtunes	206 = 64000000
Decenas de millón	107 = 10000000	Kinchiltunes	207 = 1280000000
Centenas de millón	108 = 100000000	Alautunes	208 = 25600000000

Luego el número 6HF representa 6 tunes más H uinales más F kines; o dicho de otra manera 6 tunes más 17 uinales más 15 kines.

En realidad el sistema Maya de numeración utilizado para cálculos calendáricos no era exactamente vigesimal, ya que cada tun equivalía a 18 uinales, pero aquí usaremos un sistema estrictamente vigesimal, totalmente regular y más apto para cálculos con el ábaco Nepohualtzintzin.

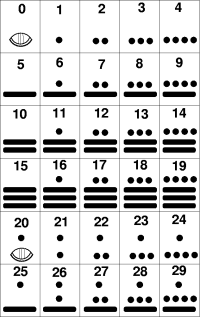
Los Mayas representaban los números de dos formas diferentes. Una de ellas era empleando 20 glifos diferentes que representan caras de perfil. Esta notación era usada en monumentos. La otra forma estaba constituida por puntos, con valor 1, y por rayas, con valor 5. El cero se representaba por medio del símbolo de una concha.

Si el número estaba formado por más de una cifra, se colocaban verticalmente, con los kines en la parte inferior.

Abaco Nepohualtzintzin

Con el sistema numérico vigesimal los Mayas podían efectutar las operaciones matemáticas fundamentales por medio de tablas de sumar y de multiplicar y con la utilización de un ábaco constituido por una cuadrícula hecha con varillas, o dibujado directamente en el suelo, y se utilizaban piedrecillas o semillas para representar los números. Este ábaco recibía el nombre de Nepohualtzintzin.

En la parte superior de cada varilla tiene tres cuentas, cada una de ellas con valor de cinco unidades (una mano). En la parte inferior hay cuatro cuentas, cada una de ellas con valor de una unidad (un dedo). Las cuentas sólo tienen valor cuando est�n apoyadas en la barra central.

Una construcción moderna y utilizable del ábaco Nepohualtzintzin es el mostrado en la imagen, construido por el autor de esta página. Su manejo es similar al del ábaco Japonés Soroban, aunque tiene dos cuentas más con valor 5 debido a que se opera en el sistema vigesimal. En la imagen se muestra el número 38C (ó 3.8.12), cuyo valor en el sistema decimal es 1372.

En el Nepohualtzintzin de la imagen, con 8 varillas, se podrían hacer cálculos con números inferiores a JJJJJJJJ (ó 19.19.19.19.19.19.19.19) que en el sistema decimal es 25 599 999 999.

Además, si se dejan sin uso las dos cuentas o bolas superiores, se puede usar como si fuese un Soroban en el sistema decimal. Conviene profundizar en el estudio de las operaciones en el sistema decimal usando un Soroban antes de abordar las operaciones en el sistema vigesimal en un Nepohualtzintzin. De este modo se podrá hacer la transición con facilidad. Cualquier operación que se pueda hacer en un Soroban se puede hacer en un Nepohualtzintzin, la metodología es similar, sólo al principio operar en el sistema vigesimal resulta un poco extraño por no estar acostumbrados a él y no sabernos las tablas de sumar y de multiplicar de memoria, como sí ocurre en el sistema decimal estudiado desde la infancia en las escuelas.

Es fácil construir un Nepohualtzintzin con básicos conocimientos de bricolage, pero también se puede construir simplemente cambiando la posición de la barra central de un ábaco Chino Suanpan, que tiene disposición de cuentas 2/5, para dejarlo en la disposición 3/4 del ábaco Nepohualtzintzin.

Puede practicar con un ábaco Nepohualtzintzin virtual accesible aquí. Se necesita tener instalado JAVA. El programa permite usar todo tipo de ábacos reales o incluso otros según las preferencias del usuario. Para usar un Nepohualtzintzin elija la opción Japanese y la base 20. En la barra central hay un cursor que marca la posición del punto o coma que separa la parte entera del número de la decimal (mejor dicho: vigesimal), puede moverlo con el ratón al lugar deseado.

El máximo honor que se puede hacer a los conocimientos de otras civilizaciones es no olvidarlos. El ábaco Nepohualtzintzin merece un lugar junto al Soroban Japonés, el Suanpan Chino, el Schoty Ruso y otras variantes de los anteriores.

Por cierto, ¿qué número está escrito en el Nepohualtzintzin de la imagen?

¿Cómo se escribir�a 2005 en el ábaco Nepohualtzintzin?