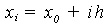Interpolation by Finite Differences

When the interpolation points are equally spaces, the values of the interpolation polynomial can be expressed in terms of finite differences. Suppose that for , where h is the grid size, the values 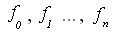of the function f(x) are known. The difference are then called finite differences of first order. Furthermore, we define the differences of order k + 1 inductively by . If we use the shift operator E defined by 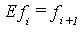, the difference operator is represented as . 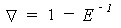Sometimes the backwards difference is 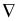, the operator is called the forward difference. 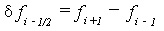The central difference which is defined by is also used.

Table 1 shows the relations between the finite differences and the differentiation operator D defined by .

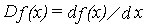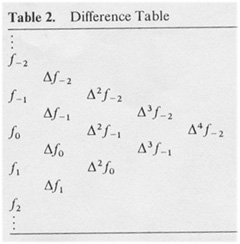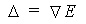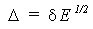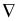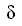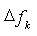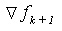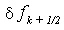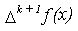Table 2, in which each entry after the second column is the or we can express each entry of table 2 in terms of or . For example, in the second column, is equal to and . If f(x) is a polynomial of degree k, then f(x) is a polynomial of degree is a constant, and is zero. Therefore, looking at the difference table, we can find the degree of an interpolation polynomial that can satisfactory approximate f(x). It should also be noted that, if the computation of each entry of the table is carried out with a finite number of significant figures, the error in the values 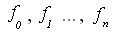is multiplied by binomial coefficients corresponding to the location in the difference table.

The following are interpolation formulas for which the difference table is used. Suppose that we want to interpolate the value 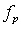at 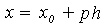. Then from 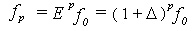, we have Newton's forward interpolation formula: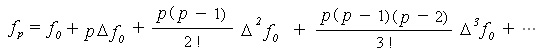

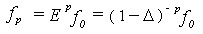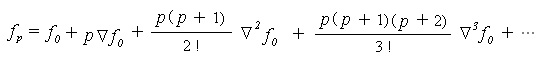
Similarly, from , we have Newton's backward interpolation formula: 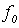We get these formulas by starting at and proceeding downward to the right or upward to the right. On the other hand, by proceeding in a zigzag manner, downward to the right, then upward to the right, then again downward it the right, etc., we get another formula, called Gauss's forward interpolation formula: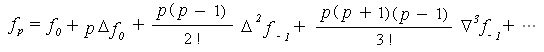

Similarly, we have Gauss's backward interpolation formula:
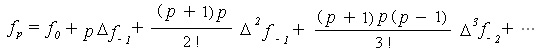
In addition to these formulas, there are several by Everett, Bessel, Stirling, and others, which are essentially equivalent to the Lagrange interpolation polynomial that uses the same tabular points, although the representations are different.