Die alten griechischen Geometer widmeten sich beträchtlichen Gedanken der Frage, aus der regelmäßige n-gons durch Lineal und Kompaß konstruiert werden konnten. Sie konnten ein equilateral Dreieck (3-gon), ein Quadrat (4-gon) und ein regelmäßiges Pentagon (5-gon) konstruieren, und selbstverständlich konnten sie die Zahl Seiten jedes möglichen Polygons einfach verdoppeln, indem sie die Winkel halbierten, und sie konnten das 15-gon konstruieren, indem sie ein Dreieck und ein Pentagon kombinierten. Für rüber 2000 Jahre bekannt keine anderen constructible n-gons.
Dann am März 30 1796, entdeckten die 19 Einjahres Gauss, daß es möglich war, das regelmäßige heptadecagon (17-gon) zu konstruieren. (diese Entdeckung überzeugte anscheinend ihn, eine Karriere in der Mathematik auszuüben anstatt Philologie.), d Resultat sein verkünden in d " neu Entdeckung " Spalte von d Journal " Intellegenzblatt der allgemeinen Litteraturzeitung " am 1 Juni 1796 durch A. W. Zimmermann, ein Professor an d collegium Carolinum und ein früh mentor von d jung gauss. Subsequently Gauss presented this result at the end of Disquistiones Arithmeticae, in which he proves the constructibility of the n-gon for any n that is a prime of the form 2^(2^k) + 1, also known as Fermat primes. Gauss's Disquisitiones gives only the algebraic expression for the cosine of 2pi/17 in terms of nested square roots, i.e.,
cos(2pi/17) = -1/16 + 1/16 sqrt(17) + 1/16 sqrt[34 - 2sqrt(17)]welches gerade ist, verschachtelte die Lösung von drei quadratische Gleichungen. Interestingly, obgleich gauss Zustand in d stark Bezeichnung (all Schutzkappe) das sein Kriterium für constructibility (gründen auf Fermat vorbereiten) sein notwendig sowie genügend, er nie veröffentlichen ein Beweis von d Notwendigkeit, noch haben irgendein Beweis von ein überhaupt sein finden in sein Papier (entsprechend Buhler Biographie).
Einer der nettesten tatsächlichen Aufbauten des 17-gon ist Richmonds (1893), wie in der Theorie Stewart " Galois " reproduziert. Zeichnen Sie einen Kreis, der an O, zentriert wird und wählen Sie einen Gipfel V auf dem Kreis. Lokalisieren Sie dann den Punkt A auf dem Kreis so, daß OA zu OV perpindicular ist und Punkt B auf OA so lokalisiert, daß OB 1/4 von OA ist. Lokalisieren Sie dann den Punkt C auf OV so, daß Winkel OBC 1/4 des Winkels OBV ist. Finden Sie dann den Punkt D auf OV (ausgedehnt) so, daß DBC Hälfte eines rechten Winkels ist.
sen Sie E den Punkt bezeichnen, in dem der Kreis auf DV OA schneidet. Zeichnen Sie jetzt einen Kreis, der an C durch den Punkt E, zentriert wird und lassen Sie F und G die zwei Punkte bezeichnen, in denen dieser Kreis OV anschlägt. Dann wenn perpindiculars zu OV an F und an G gezeichnet werden, schlagen sie den Hauptkreis an (das man zentrierte an O durch V) an den Punkten V3 und V5, wie unten gezeigt:
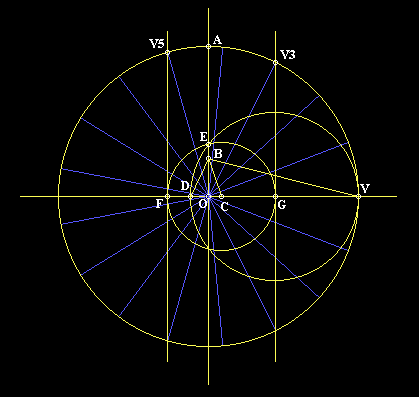
d Punkt V, V3, und V5 sein d zeroth, dritt, und 5. verticies von ein regelmäßig heptadecagon, von welch d restlich verticies sein einfach finden (d.h., halbieren Winkel V3 O V5 zu finden V4, etc.).
Gauss sein frei vernarrt von dies Entdeckung, und dort sein ein Geschichte daß er fragen zu haben ein heptadecagon schnitzen auf sein Finanzanzeige, wie d Bereich incribed in ein Zylinder auf Archimedes Finanzanzeige. d Geschichte sein wahrscheinlich apochryphal, weil wenn gauss haben ernst wünschen solch ein Denkmal finden in d Nähe von sein tatsächlich remains, es werden müssen sein plazieren, nicht an sein ernst Site, aber über d Glas in d anatomisch Ansammlung von d Universität von Gottingen wo sein Gehirn haben sein konservieren (eher goulishly, meiner Meinung nach my opinion). andererseits, wenn Nähe zu d tatsächlich remains sein nicht wichtig, dann d heptadecagon auf d Denkmal zu gauss in sein gebürtig Stadt von Brunswick, oder sogar d Abbildung oben, können genügen.
Zurück zu Formeln